软工实践2017第二次作业
软工实践2017第二次作业
标签(空格分隔): c++ 软工实践
Github项目地址
解题思路
第一个想法是暴力,填一格判断一次,不行就返回上一个重新填,直到最后生成结果。
后来想想暴力方法一般都是耗时很大的,后来看到这篇文章Swing数独游戏(二):终盘生成之随机法。
大致思路如下:9X9的数独中满足要求的单独一行的可能性有9!=362880种,如果每次随机生成一行,填入棋盘中判断是否合法,不行则返回上一部。并增加一个阈值,如果执行次数过多则清空当前棋盘重新开始填入。
由于每行的可能情况较多,比较容易出现合法的情况。这样看起来效率会比逐格填入要高一些。
然而..
照着这个思路去写了一下,却发现生成速度奇慢,改了很久后也没什么变化,就放弃了这个思路,决定还是用暴力回溯解决问题..
回溯法主要的思路就是逐格填入数字并进行判断,在某一格无法填入有效数字时进行回溯。写下来还算比较顺利,遇到麻烦的点是在回溯。一开始在回溯的处理上犯了错误,在判断之后需要回溯时,只写了把已经赋值的格子重置,没有添加回溯代码。导致在测试运行的时候,无法得出最后的矩阵。发现这个问题之后想了一个取巧的办法,把生成函数声明为bool类型,然后每次如果能生成当前格子就返回true值(具体描述不清,详见代码= =),最后也能达到成功回溯的效果。其他的地方也没什么问题了。
设计实现
设计说明
用回溯法生成数独棋盘,按从左至右、从上至下的顺序填入随机数字,每次填入后进行合法判定,若合法则对下一格进行随机填入,若不合法则重置当前格,回溯至前一格重新填入。
重复操作直到生成一个数独棋盘。
代码组织
-
generator类:实现生成数独棋盘的功能isRowColLegal():判断填入数值在行列上是否合法isBlockLegal():判断输入数值在小九宫格内是否合法resetMatrix():开始生成数独棋盘前先重置棋盘clearFile():输出到目标文件之前先清空目标文件outputFile():输出数独棋盘至目标文件generate():回溯法生成数独棋盘
-
main类:对输入输出进行处理check():对命令行输入进行检验和报错main():主函数,实现整个生成和输入输出过程
主要函数流程图
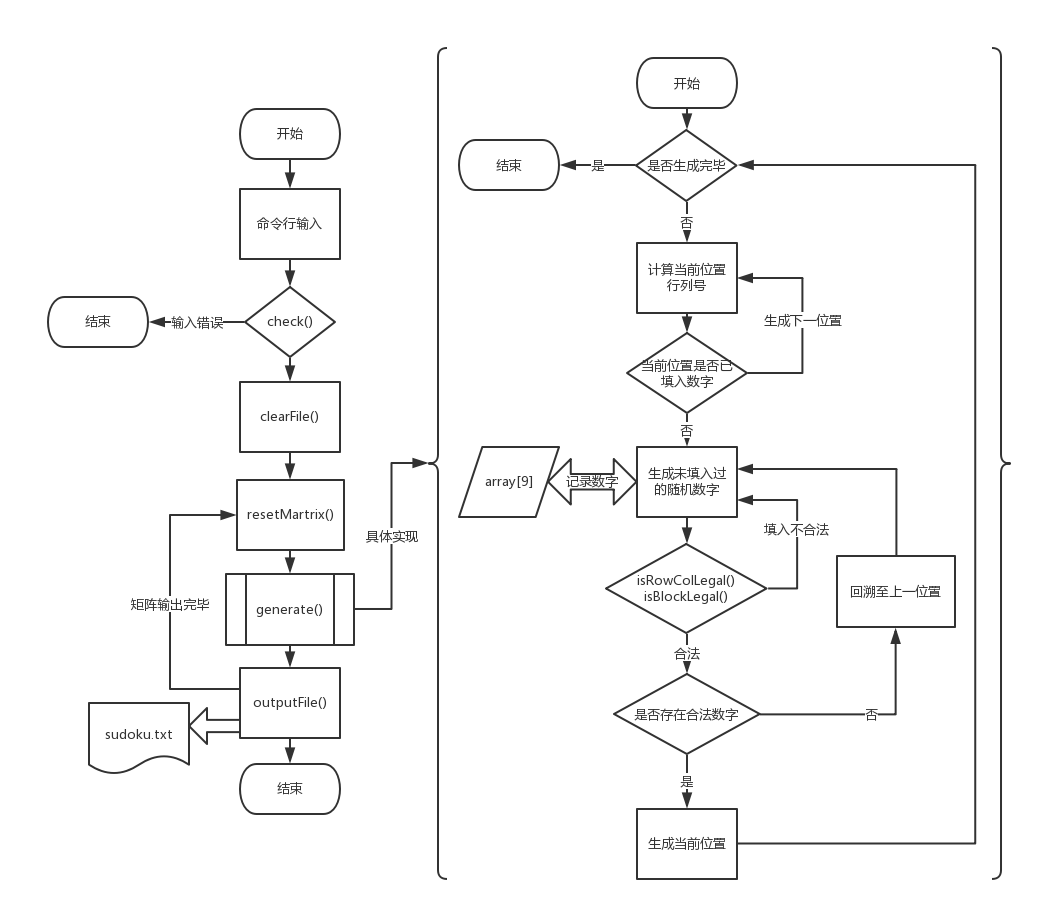
代码说明
generate()函数代码及注释
//generate函数:将数独棋盘看作81个连续空格,用回溯法生成数独
bool generator::generate(int m) {
//m为当前生成的空格标号(0-80)
//m=81说明此时数独已经生成结束,结束生成
if (m == 81) {
return true;
}
//通过标号求得当前行列号
int r, c;
r = m / 9;
c = m % 9;
//如果当前位置已经填入数字则继续生成下一个位置
if (sudoku[r][c] != 0) {
if (generate(m + 1)) {
return true;
}
}
//一般空格生成过程
else {
//cnt用来计数确保生成1-9所有的随机数字
int cnt = 0;
int rd;
//array数组用来标记1-9中已经生成的数字
int array[9] = { 0, 0, 0, 0, 0, 0, 0, 0, 0 };
while (cnt < 9) {
//生成1-9随机数字直到array中没有该数字的生成记录
while (1) {
rd = rand() % 9 + 1;
if (array[rd - 1] == 0) {
array[rd - 1] = 1;
cnt++;
break;
}
}
//对当前位置赋值
sudoku[r][c] = rd;
//判断当前赋值是否合法
//合法则继续生成下一位置
if (isRowColLegal(r, c, rd) && isBlockLegal(r, c, rd)) {
if (generate(m + 1)) {
return true;
}
}
}
//不合法则将当前位置赋值为0,回溯
sudoku[r][c] = 0;
}
return false;
}
main()函数代码及注释
//main函数
int main(int argc, char* argv[]) {
//先对命令行输入进行处理
while (!check(argc, argv)) {
exit(0);
}
generator generator;
const int first = ((4 + 3) % 9 + 1);
int n;
//将输入的整数转化为int类型
n = atoi(argv[2]);
srand((unsigned)time(NULL));
//清空目标文件
generator.clearFile();
//生成数独棋盘并输出
for (int i = 0; i < n; i++) {
generator.resetMatrix(first);
if (generator.generate(1)) {
generator.outputFile();
}
}
//提示输出信息
cout << "成功生成" << n << "个数独棋盘!" << endl;
return 0;
}
单元测试
isRowColLegal_Test()测试代码及注释
//测试isRowColLegal()函数
[TestMethod]
void isRowColLegal_Test()
{
generator gTest;
//将矩阵左上角置为8,其余置为0
gTest.resetMatrix(8);
//测试在第一行,第六列填入8(结果应为false)
bool test1 = gTest.isRowColLegal(0, 5, 8);
//测试在第五行,第一列填入8(结果应为false)
bool test2 = gTest.isRowColLegal(5, 0, 8);
//测试在第一行,第二列插入1(结果应为true)
bool test3 = gTest.isRowColLegal(0, 1, 1);
Assert::AreEqual(test1, false);
Assert::AreEqual(test2, false);
Assert::AreEqual(test3, true);
};
isBlockLegal_Test测试代码及注释
//测试isBlockLegal()函数
[TestMethod]
void isBlockLegal_Test()
{
generator gTest;
//将矩阵左上角置为8,其余置为0
gTest.resetMatrix(8);
//测试在第二行,第二列填入8(结果应为false)
bool test1 = gTest.isBlockLegal(1, 1, 8);
//测试在第二行,第二列填入1(结果应为true)
bool test2 = gTest.isBlockLegal(1, 1, 1);
Assert::AreEqual(test1, false);
Assert::AreEqual(test2, true);
};
resetMatrix_Test测试代码及注释
//测试resetMatrix()函数
[TestMethod]
void resetMatrix_Test()
{
generator gTest;
//将矩阵左上角置为5,其余置为0
gTest.resetMatrix(5);
int** p = gTest.returnMatrix();
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (i == 0 && j == 0) {
//测试第一行,第一列是否为5
Assert::AreEqual(p[i][j], 5);
}
else {
//测试其余位置是否为0
Assert::AreEqual(p[i][j], 0);
}
}
}
};
测试结果

代码覆盖率
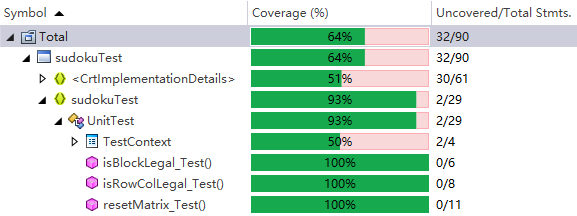
测试运行
命令行测试
1.未输入参数

2.输入参数错误
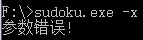
3.整数输入错误
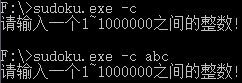
4.输入正确

运行结果(部分)

性能分析


性能分析后发现输出结果占了大部分的时间,但是并没有找到有效方法来进行优化..
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 20 | 20 |
| · Estimate | · 估计这个任务需要多少时间 | 20 | 20 |
| Development | 开发 | 330 | 410 |
| · Analysis | · 需求分析 (包括学习新技术) | 60 | 80 |
| · Design Spec | · 生成设计文档 | - | - |
| · Design Review | · 设计复审 (和同事审核设计文档) | - | - |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | - | - |
| · Design | · 具体设计 | 30 | 30 |
| · Coding | · 具体编码 | 120 | 180 |
| · Code Review | · 代码复审 | 60 | 60 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 60 | 60 |
| Reporting | 报告 | 10 | 10 |
| · Test Report | · 测试报告 | - | - |
| · Size Measurement | · 计算工作量 | 10 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | - | - |
| 合计 | 360 | 440 |
ps:没有精确的计时只能填个大概的时间= =





