数据结构——堆排序

系列文章：数据结构与算法系列——从菜鸟到入门 

什么是堆？

堆数据结构是一种数组对象，它可以被视为一棵完全二叉树。树中每个节点与数组中存放该结点值的那个元素对应。树的每一层都是填满的，最后一层可能除外（最后一层从最结点的左子树开始填）。如果给定了某个结点的下标 i，那么其父结点为 PARENT(i)=i/2（向下取整），其左儿子结点为 LEFT(2i)，其右儿子结点为 RIGHT(2i+1)。

最小堆与最大堆（小根堆、大根堆）

二叉堆有两种：最小堆和最大堆。
在最大堆中，最大堆特性是指除了根以外的每个结点 i，有 A[PARENT(i)]>=A[i]，即某个结点的值至多是和其父结点的值一样大。堆中的最大元素就存放在根结点中；并且，在以某一个结点为根的子树中，各结点的值都不大于该子树根结点的值。

最小堆则相反，最小堆特性是指除了根以外的每个结点 i，有 A[PARENT(i)]<=A[i]，最小堆的最小元素是在根部。

堆排序的基本过程

堆排序的基本思想是，将待排序数组构造成大根堆，此时，整个数组的最大值就是堆顶结点。将堆顶与堆末尾结点交换，此时数组的最大值就处在了数组末尾位置，然后将 0~n-1 的结点构造为大根堆，并再次将堆顶结点与堆尾的 A[A.length-2]结点交换，至此数组的最大和次大的两个元素就排在了数组的末尾，如此反复执行就得到了升序排序的数组。

• MAX-HEAPIFY 过程，其运行时间为 O(lgn)，是保持最大堆性质的关键；
• BUILD-MAX-HEAP 过程，以线性时间运行，可以无序的输入数组基础上构造出最大堆；
• HEAPSORT 过程，运行时间为 O(nlgn)，对一个数组原地进行排序。

下面对这三个过程一一分析。

保持堆的性质（MAX-HEAPIFY） 

/**
 * 保持堆的性质*/
private void MAX_HEAPIFY(int[] A, int i, int end) {
    int l = LEFT(i);
    int r = RIGHT(i);
    int largest;
    if (l <= end && A[l] > A[i]) {
        largest = l;
    }else {
        largest = i;
    }
    if (r <= end && A[r] > A[largest]) {
        largest = r;
    }
    if (largest != i) {
        swap(A, i, largest);
        MAX_HEAPIFY(A, largest, end);
    }
}

/**
 * 左结点 */
private int LEFT(int i) {return 2*i+1;}

/**
 * 右结点 */
private int RIGHT(int i) {return 2*i+2;}

其输入为数组 A 和下标 i。当其被调用时，假定 LEFT(i) 和 RIGHT(i) 为根的两棵二叉树都是最大堆，但 A[i]可能小于其子女，这违反了最大堆性质。
MAX-HEAPIFY 让 A[i]在最大堆中“下降”，使以 i 为根的子树成为最大堆。

从元素 A[i]，A[LEFT(i)]和 A[RIGHT(i)]中找出最大的，将其下标保存至 largest 中。如果 i==largest，即 A[i]是最大的，则以 i 为根的子树已是最大堆，程序结束。否则，i 的某个子节点中有更大的元素，则与 i 交换，从而使 i 及其子女均满足堆性质。下标 largest 的结点在交换后的值是 A[i]，以该结点为根的子树又有可能违犯最大堆性质。因而递归地，对 largest 子树调用 MAX-HEAPIFY。

 

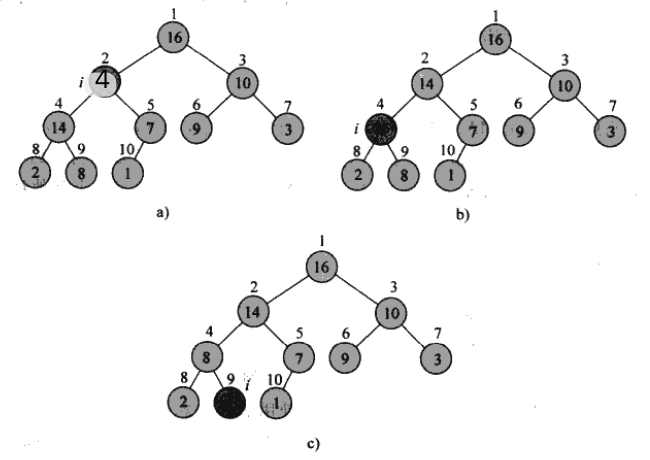
上图反映的是调用 MAX-HEAPIFY(A, 2, length(A)-1)。a) 初始构造，i=2处的结点违反了大根堆性质。b) 挑选 A(2)的左右孩子中最大的一个，即 A(4)，将 A(2)与 A(4)交换，而后发现以 A(4)为根的子树不满足大根堆的性质，A(9)大于 A(4)。c) 和 b 过程类似的，将 A(9)与 A(4)交换，此时整个完全二叉树即符合了大根堆的性质。

建堆（BUILD-MAX-HEAP）

/**
 * 建堆*/
private void BUILD_MAX_HEAP(int[] A) {
    for (int i = A.length/2-1;i >= 0;i--) {
        MAX_HEAPIFY(A, i, A.length-1);
    }
}

运用 MAX-HEAPIFY 来自底向下地将一个数组 A[1..n]变成一个最大堆。
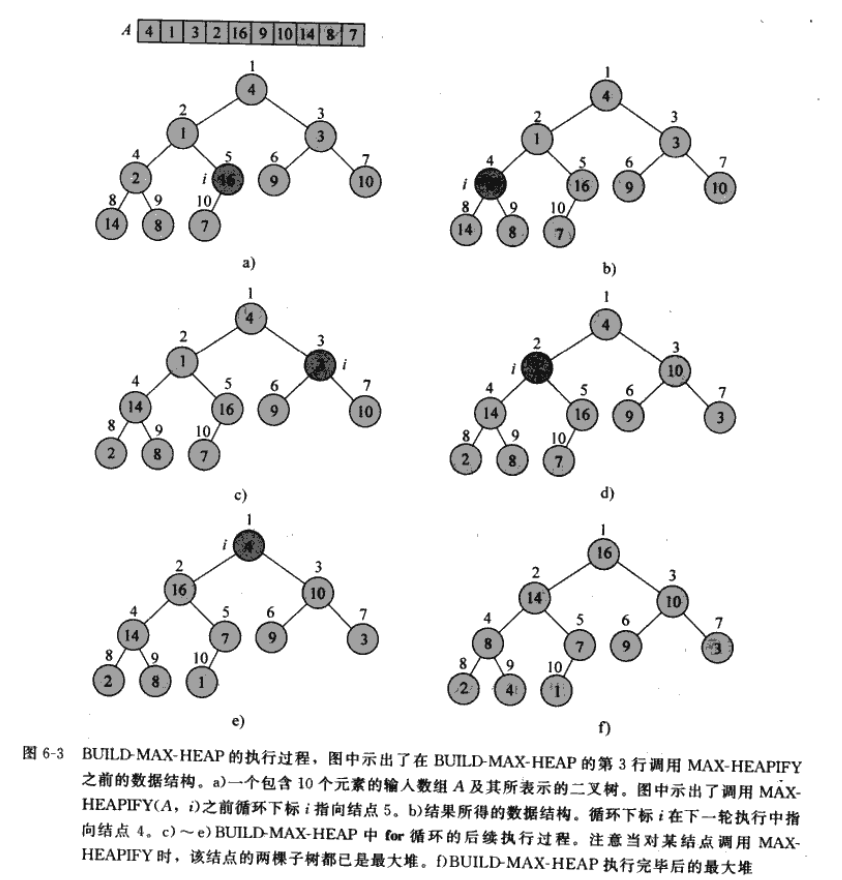
从 length[A]/2-1 到 0 遍历数组，调用 MAX-HEAPIFY，将以该结点为根的子树调整为符合大根堆性质。过程如下图所示，不再赘述：

堆排序算法（SORT-HEAP）

/**
 * 堆排序
 */
private void SORT_HEAP(int[] A) {
    for (int i = A.length-1;i >=0;i--) {
        swap(A, 0, i); // 将堆尾和堆顶交换
        // 0~length(A)-1 的堆，重新建堆，经过交换，堆不再符合大根堆
        MAX_HEAPIFY(A, 0, i-1);
    }
}

堆排序算法先用 BUILD-MAX-HEAP 将输入数组 A[1..n]构造成一个最大堆。因为 A[1]是数组中最大，所以将 A[1]与 A[n]交换，A[1]也就处在了升序排序的正确位置，接下来将 A[1..n-1]的重新调整为最大堆，将 A[1]与 A[n-1]交换，也就将数组中倒数第二大的数放在了正确的位置，堆排序算法不断重复这个过程，堆的大小由 n-1 一直降到 2，就得到了数组的升序排序。

算法分析

时间复杂度：O(nlgn)。其中调用 BUILD-MAX-HEAP 的时间为 O(n)，n-1 次的 MAX_HEAPIFY 调用中每一次的时间代价为 O(lgn)。

空间复杂度：堆排序时就地排序，辅助空间为 O(1)。

稳定性：它是不稳定的排序方法。

参考资料

[1] 数据结构与算法分析——Java语言描述, 7.4.2 - 堆排序

[2] 算法导论, 6.4 - 堆排序算法