数据结构——快速排序

系列文章：数据结构与算法系列——从菜鸟到入门

描述

快速排序是基于分治模式的，下面按分治模式来进行分析：

分解：

　　数组 A[p..r]被划分成两个（可能空）子数组，A[p..q-1]和 A[q+1..r]，使得 A[p..q-1]中的每个元素都小于等于 A(q)，也小于等于 A[q+1..r]中的元素。

解决：

　　递归的对子数组 A[p..q-1]和 A[q+1..r]进行再排序。

合并：

　　子数组是就地排序，不需要合并操作，整个数组 A[p..r]已有序。

伪代码：

quickSort(int[] A, int left, int right) {
    if (left >= right) {
        return;
    }
    int res = partition(A, left, right); // 划分区间，返回中位数
    quickSort(A, left, res-1); // 递归划分后的左区间
    quickSort(A, res+1, right); // 递归划分后的右区间
}

数组的划分过程（PARTITION）

PARTITION 过程：

　　它对子数组 A[p..r]进行就地重排序。

伪代码：

方法1.单向扫描

定义临时变量 j，用于遍历待排序数组，将小于等于 res 的 A[j]与 A[i]交换，这里的临时变量 i 就是保存下次交换的位置。最终小于等于 res 的元素被全部交换到了数组的前面，操作的最后，将 res 交换到数组中最后一个小于等于它的元素的后面。这样数组就分为了三个子区间，小于等于 res 区间，res 本身区间，大于 res 区间。接着，对非 res 本身的另两个区间进行递归地同样操作。

private static int partition1(int[] A, int left, int right) {
    int res = getStandard(A, left, right); // 获取基准位
    int i = left;
    int num = A[res];
    swap(A, right, res);
    for (int j = left;j < right;j++) {
        if (A[j] <= num) {
            swap(A, j, i++);
        }
    }
    swap(A, right, i);
    return i;
}

 方法2.双向扫描

详情看这里：快速排序图文说明，不再重造轮子。网上博客大部分都是这样写的。

private static int partition2(int[] A, int left, int right) {
    int l = left;
    int r = right;
    int res = A[left];
    while (l < r) {
        while (l<r && A[r]>res) {
            r--;
        }
        if (l < r) {
            A[l++] = A[r];
        }
        while (l<r && A[l]<res) {
            l++;
        }
        if (l < r) {
            A[r--] = A[l];
        }
        A[l] = res;
    }
    return l;
}

性能分析

快速排序的平均比较次数为 O(nlgn)，时间复杂度为 O(nlgn)。

最坏情况：

最坏情况是，当序列已排序时，如：

{1,2,3,4,5,6,7,8}

选取序列的第一个值作为基准值，分成的两个子序列长度为 1 与 n-1：

1,{2,3,4,5,6,7,8}

这样必须经过 n-1 趟才能完成排序。因此，总的比较次数为：

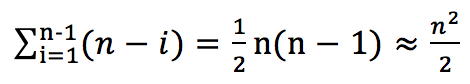
所以最坏的时间复杂度为O(n^2)

最佳情况：

在最好情况下，每次划分所取得基准都是当前无序区的“中值”记录，划分的结果是基准的左、右两个无序区间的长度大致相等。总的关键字比较次数为：O(nlgn)

下面从递归树的角度再分析，每次划分后，左、右子区间长度大致相等，根据二叉树的性质，递归树的高度为 O(lgn)，而递归树每一层上各节点对应的划分过程中所需要的关键字比较次数总和不超过 n，故整个排序过程所需要的关键字比较总次数为 O(nlogn)

空间复杂度：

快速排序在系统内部需要一个栈来实现递归。若每次划分较为均匀，则其递归树的高度为 O(lgn)，故递归后需栈空间为 O(lgn)。最坏的情况，递归树的高度为 O(n)，所需的栈空间为 O(n)。

稳定性：

快速排序是非稳定的。

基准的选取

在当前无序区中选取划分的基准关键字是决定算法性能的关键。以下两种方式都是为了优化，选取固定基准所产生的最坏情况。

“三者取中”：

即在当前区间里，将该区间首、尾和中间位置上的关键字比较，取三者的中值所对应的记录作为基准。

private static int getStandard(int[] A, int left, int right) {
　　 // 三者取中（直接将三者交换排序，返回中间位置）
    int middle = left+(right-left)/2;
    int a = A[left],b = A[right],c = A[middle];
    if (a > b) {swap(A, left, right);}
    if (a > c) {swap(A, left, middle);}
    if (b > c) {swap(A, right, middle);}
    int res = middle;
    return res;
}

“随机选择”：

取位于 low 和 high 之间的随机数 k(low<=k<=high)，用 R[k] 作为基准，这相当于强迫 R[low....high] 中的记录是随机分布的。

private static int getStandard(int[] A, int left, int right) {
    // 选取基准关键字 —— 取随机数
    int res = new Random().nextInt(right-left)+left;
    return res;
}

参考资料

[1] 数据结构（Java版）, 3.3.2 - 快速排序

[2] 数据结构与算法分析——Java语言描述, 7.3.2 - 快速排序

[3] 算法导论, 7.4 - 快速排序分析