自信息、信息熵和相对熵

参考：https://blog.csdn.net/happyhorizion/article/details/77894051

https://blog.csdn.net/acdreamers/article/details/44657745

 

1、自信息

一件事发生的概率越大，其所带的信息量就越小，反之发生的概率越小，信息量就越大。[可以这么理解，对于一件发生概率极低的事情，我们想让他发生，就要去找大量信息]

自信息就是以概率p(x)观察到某一事件发生所携带的信息量，自信息也是概率越大信息量就越小，也可以理解为某个概率事件进行编码所需要的最小编码长度

2、信息熵／香农熵

熵是平均自信息量，衡量一件事情发生的不确定性，可以这么理解对于一件事在不同概率下发生都会产生一定的信息量，而熵就是携带的平均信息量。

对于连续值来说：

 

对于离散值来说：

，其中k常数

3、互信息 

对于x来说，它的的不确定性，即熵为H(x), 当已知事件y的不确定性H(y)后，x的不确定性的减少量就是互信息，I(x, y) = H(x) - H(x | y) 

 

4、交叉熵

    假设有两个分布p(x) 和 q(x)，其中p(X) 是事件的真实分布，则该事件的熵，即不确定性为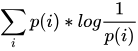，那么如果用q(x) 来进行对该事件进行预测，则其预测出来的不确定性为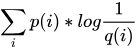，称为交叉熵，记作H(p, q), 即用一个非真实的概率分布q(X)对真实事件进行编码所用的平均长度。

    交叉熵越小，说明q(x) 越接近真实概率，

 

5、相对熵（KL散度）

    参考：https://www.cnblogs.com/bnuvincent/p/6940863.html

            https://www.zhihu.com/question/41252833

相对熵就是 对事件用q(x) 进行编码 比 真实编码 所增加的字节长度， 也就是 交叉熵 - 熵；

互信息衡量两个随机变量之间的关系，引入某一个变量后，另一个变量减少的程度。而相对熵就是衡量两个分布之间的关系

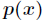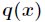设和是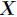取值的两个概率概率分布

 

 

           上式中第二项就是交叉熵，

 

   在一定程度上，熵可以度量两个随机变量的距离。KL散度是两个概率分布P和Q差别的非对称性的度量。KL散度是用来度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下，P表示数据的真实分布，Q表示数据的理论分布，模型分布，或P的近似分布。