命令行参数
实验要求
提交测试结果截图,课下把代码上传到码云。
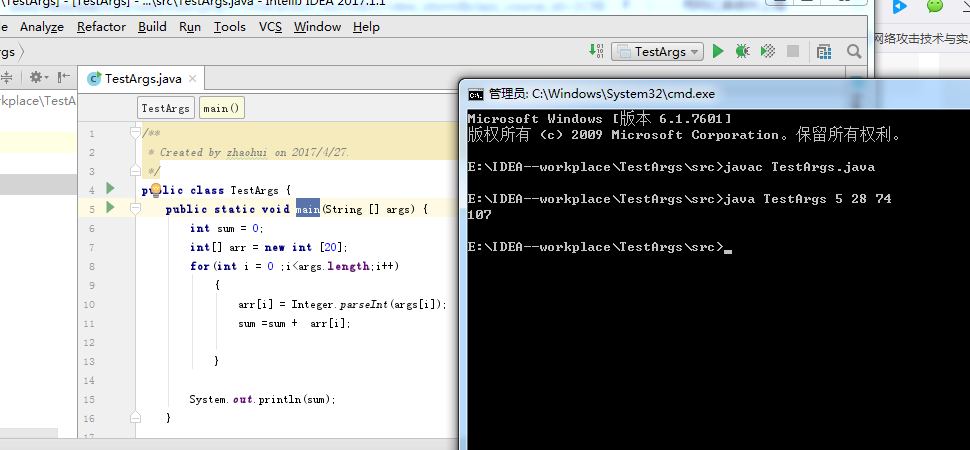
求命令行传入整数参数的和。
public class TestArgs {
public static void main(String [] args) {
int sum = 0;
// 参考Integer类中的方法把字符串转为整数
// 补充代码求命令行参数的args中整数数据的和
// 打印
System.out.println(sum);
}
}
-
java中String字符串转化为数字:
转换为浮点型:
使用Double或者Float的
parseDouble或者parseFloat方法进行转换String s = "123.456 "; //要确保字符串为一个数值,否则会出异常
double d = Double.parseDouble(s);
float f = Float.parseFloat(s);转换为整型:
使用```Integer```的```parseInt```方法进行转换。int i = Integer.parseInt([String]);//[String]待转换的字符串
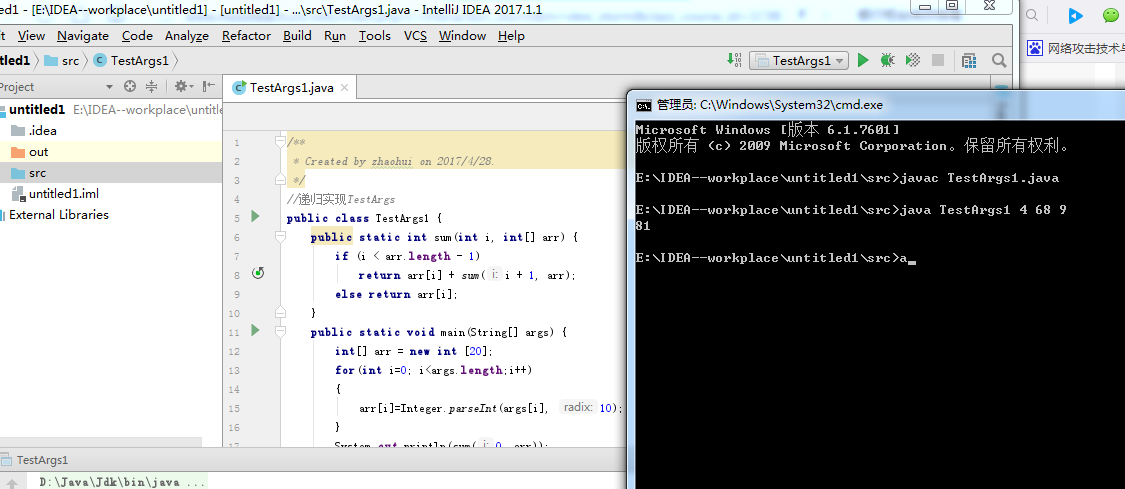
递归方式
实验要求
public class TestArgs {
public static void main(String [] args) {
int sum = 0;
// 参考Integer类中的方法把字符串转为整数
// 补充代码以递归的方式求命令行参数的args中整数数据的和
// 打印
System.out.println(sum);
}
//递归函数
public static void clSum(int [] arr) {
}
}
- 递归实现可以用阶乘的原理理解或者用组合数学的递推关系来理解。
- 阶乘理解:f(n)=n!;
(n+1)!=(n+1)n!=(n+1)f(n); - 递推关系:
Hanoi问题:这是个组合数学中的著名问题.N个圆盘依其半径大小,从下而上套在A柱上,如下图示.每次只允许取一个移到柱B或C上,而且不允许大盘放在小盘上方.若要 求把柱A上的n个盘移到C柱上请设计一种方法来,并估计要移动几个盘次.现在只有A、B、C三根柱子可用.
算法分析:令h(n)表示n个圆盘所需要的转移盘次。根据算法先把前面n-1个盘子转移到B上;然后把第n个盘子转到C上;最后再一次将B上的n-1个盘子转移到C上。
n=2时,算法是对的,因此,n=3是算法是对的。以此类推。于是有: h(n)=2h(n-1)+1,h(1)=1
- 阶乘理解:f(n)=n!;
实验三 敏捷开发与XP实践
凯撒密码的加密算法极其简单。其加密过程如下:
在这里,我们做此约定:明文记为m,密文记为c,加密变换记为E(k1,m)(其中k1为密钥),解密变换记为D(k2,m)(k2为解密密钥)(在这里k1=k2,不妨记为k)。凯撒密码的加密过程可记为如下一个变换:
c≡m+k mod n (其中n为基本字符个数)
同样,解密过程可表示为:
m≡c+k mod n (其中n为基本字符个数)
该程序既可用于加密又可用于解密。
只要执行:明文(要加密的字符串) 密钥(移动的位数)即可加密。
在密钥前面加上负号,将运行
明文(要加密的字符串) -密钥(移动的位数)
即可解密。
如果密钥大于26,程序中移位前会和26取模而将其调整到26以下。只有知道密钥才能得到原来的密文。
因此运行:Hello World! 30
同样将输出“Lipps Asvph!”。

问题及解决
按照博客中的密码运行提示出现错误,让我想起,args的练习,找到了解决办法

- 1命令行
在java程序所在文件夹的地址栏中输入cmd
先编译javac Test.Java
再运行Java Test arg1 arg2 arg3 ……(参数之间用空格隔开) - 2 IDEA
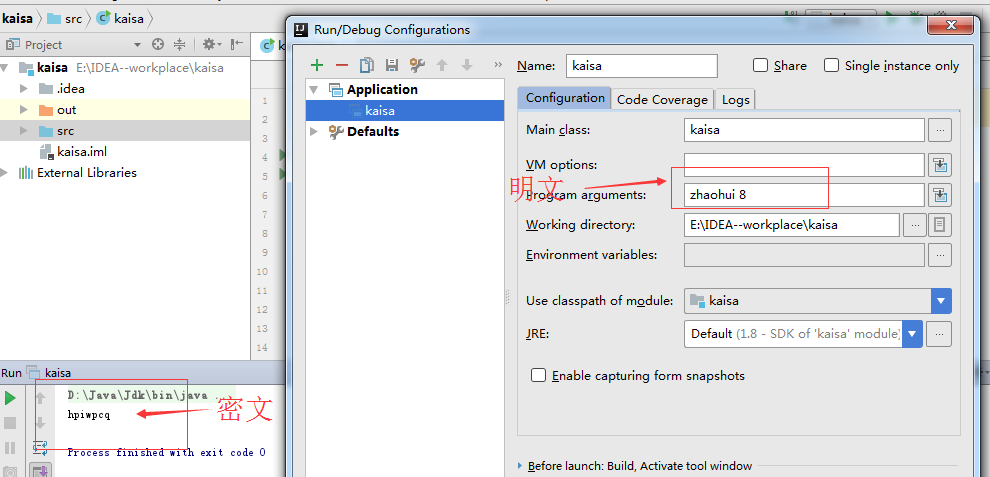
点击Run下的Edit Configurations
配置Configuration分页中的Program arguments选项,就可以在idea中传入参数,点击OK,然后从新运行。

- 小窍门:如在工作时经常要写System.out.println(); 这个在idea里已经预设好了,直接输入sout 然后按tab键就可以了,你也可以试试输入soutm,soutp加tab键
实验参考
http://www.cnblogs.com/rocedu/p/4795776.html
http://www.cnblogs.com/rocedu/p/4795776.html
http://www.cnblogs.com/rocedu/p/6683948.html
http://blog.csdn.net/sky19891212/article/details/43566493



