该程序在屏幕上画出指定的函数的图像，函数的自变量的取值范围由用户指定，程序自动计算该区间内函数的值的取值范围。首先，让我们来看一幅正弦函数: f(x) = sin(x) 的图像： 
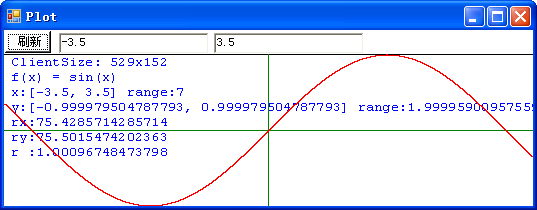
这 幅图像中，ClientSize: 529x152 表示该程序画图区宽度为 529 个像素，高度为 152 个像素。该函数自变量 x 的取值范围从 -3.5 到 3.5，函数值 y 的取值范围应该是从 -1 到 1，但因为浮点数运算误差的关系，程序计算出来的是从 -0.999979504787793 到 0.999979504787793。接下来的 rx 表示函数自变量每单位值用多少个象素表示，ry 表示函数的值每单位值用多少个象素表示，r 值如果小于1表示图形纵向被压扁，反之则被拉伸。
这是抛物线的图像吗？不，这就是我们要讨论的病态函数: f(x) = 3 * x2 + π-4 * ln[(π-x)2] + 1 在 x 位于区间 [-10, 10] 之间的图像。程序计算出来的函数在这区间的取值范围是从 1.02350355338907 到 301.052885868965。r 值是 0.0165397334645646，表明该图像被极大地压扁，也就是，实际的图像要高得多。但是，由于这个函数是病态的，程序的计算实际上是错误的， 在该区间内，函数的最小值应该是负无穷大，并且，在 π - 10-667 到 π + 10-667 这一极小区间内方程 f(x) = 0 有两个实根。让我们在 π 值附近放大图像看一看： 
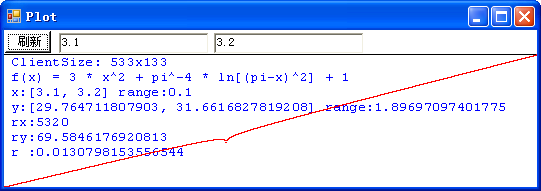
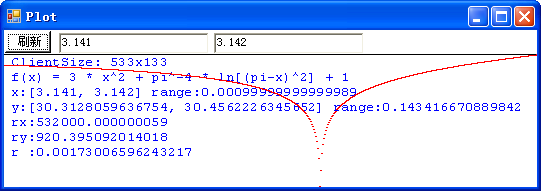
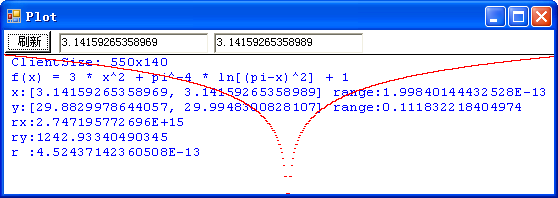
这下看得比较清楚了吧！
实际上这个病态函数是《C数值算法(第二版)》第三章“内插法和外推法”中提到的：
---------------------------------------------------------------------------
可以很容易地构造一些病态函数使内插法失败。例如，考虑函数
f(x) = 3 * x2 + π-4 * ln[(π-x)2] + 1
它 除了 x = π 之外都有定义，而 x = π 时无定义，其它情况，值有正有负。而这函数在任何基于数值 x = 3.13, 3.14, 3.15, 3.16 的插值法，都肯定在 x = 3.1416 处得到一个错误的解，尽管通过这五个点所画的曲线确实相当平滑!(用计算器试试看。)
---------------------------------------------------------------------------
这个画函数图形的C#程序有一个严重的缺点，就是函数表达式是直接写的源程序中的，不能象SciLab和Matlab那样交互式地输入。不知道用 System.Reflection.Emit.ILGenerator 类能不能动态地生成用户输入的函数表达式？好了，下面就是该程序的源代码：
// plot.cs: 画函数图形, 编译方法: csc /t:winexe plot.cs using System; using System.Drawing; using System.Windows.Forms; namespace Skyiv.Ben.Plot 
{ 
sealed class PlotForm : Form 
{ 
// 要画的函数，如果能在 TextBox 中输入函数的表达式就更好了 double Function(double x) { double u = Math.PI - x; double pi2 = Math.PI * Math.PI; return 3 * x * x + Math.Log(u * u) / pi2 / pi2 + 1; 
} // 仅仅用来显示在屏幕上 string FunctionString() { return "f(x) = 3 * x^2 + pi^-4 * ln[(pi-x)^2] + 1"; } const int yBase = 24; // 屏幕保留区域的高度 TextBox tbxX0, tbxX1; // 函数自变量的取值范围 PlotForm() { SuspendLayout(); Button btnSubmit = new Button(); btnSubmit.Text = "刷新"; btnSubmit.Location = new Point(0, 0); btnSubmit.Size = new Size(48, 24); btnSubmit.Click += new EventHandler(BtnSubmit_Click); tbxX0 = new TextBox(); tbxX0.Text = "-10"; tbxX0.Location = new Point(55, 3); tbxX0.Size = new Size(150, 20); tbxX1 = new TextBox(); tbxX1.Text = "10"; tbxX1.Location = new Point(210, 3); tbxX1.Size = new Size(150, 20); Controls.AddRange(new Control[]{btnSubmit, tbxX0, tbxX1}); Text = "Plot"; BackColor = Color.White; ClientSize = new Size(600, 600 + yBase); // WindowState = FormWindowState.Maximized; ResumeLayout(false); } void BtnSubmit_Click(object sender, EventArgs e) { Invalidate(); } protected override void OnSizeChanged(EventArgs e) { Invalidate(); base.OnSizeChanged(e); } protected override void OnPaint(PaintEventArgs e) { double x0 = double.Parse(tbxX0.Text); double x1 = double.Parse(tbxX1.Text); Graphics gc = e.Graphics; Size size = ClientSize; int i0 = 0; int i1 = size.Width - 1; int j0 = yBase; int j1 = size.Height - 1; Pen pen = new Pen(Color.Black, 1); gc.DrawLine(pen, i0, j0, i1, j0); // 画图区和保留区的分界线 double rx = (x1 - x0) / (i1 - i0); double y0, y1; GetFunctionValueRange(x0, rx, i0, i1, out y0, out y1); double ry = (y1 - y0) / (j1 - j0); Out(gc, 0, "ClientSize: {0}x{1}", i1 - i0 + 1, j1 - j0 + 1); Out(gc, 1, FunctionString()); Out(gc, 2, "x:[{0}, {1}] range:{2}", x0, x1, x1 - x0); Out(gc, 3, "y:[{0}, {1}] range:{2}", y0, y1, y1 - y0); Out(gc, 4, "rx:{0}", 1 / rx); // 函数自变量每单位值用多少个象素表示 Out(gc, 5, "ry:{0}", 1 / ry); // 函数的值每单位值用多少个象素表示 Out(gc, 6, "r :{0}", rx / ry); // 该值如果小于1表示图形纵向被压扁，反之则被拉伸 pen.Color = Color.Green; int j = j1 + (int)(y0 / ry); if (j >= j0 && j <= j1) gc.DrawLine(pen, i0, j, i1, j); // x坐标轴 int i = i0 - (int)(x0 / rx); if (i >= i0 && i <= i1) gc.DrawLine(pen, i, j0, i, j1); // y坐标轴 pen.Color = Color.Red; for (i = i0; i <= i1; i++) { double x = x0 + (i - i0) * rx; double y = Function(x); if (double.IsInfinity(y) || double.IsNaN(y)) continue; j = j1 - (int)((y - y0) / ry); if (j > j1 || j < j0) continue; gc.DrawLine(pen, i, j, i + 1, j); // 画函数的图形 } base.OnPaint(e); } // 函数值的取值范围 void GetFunctionValueRange(double x0, double rx, int i0, int i1, out double y0, out double y1) { y0 = double.MaxValue; y1 = double.MinValue; for (int i = i0; i <= i1; i++) { double x = x0 + (i - i0) * rx; double y = Function(x); if (double.IsInfinity(y) || double.IsNaN(y)) continue; if (y0 > y) y0 = y; if (y1 < y) y1 = y; } } // 在指定的位置写字符串 void Out(Graphics gc, int line, string fmt, params object [] args) { gc.DrawString(string.Format(fmt, args), new Font("Courier New", 10), Brushes.Blue, new PointF(5, yBase + 15 * line)); } static void Main() { Application.Run(new PlotForm()); } } 
} 
