51nod 2006 飞行员配对(二分图最大匹配) 裸匈牙利算法 求二分图最大匹配题

题目：

 

 

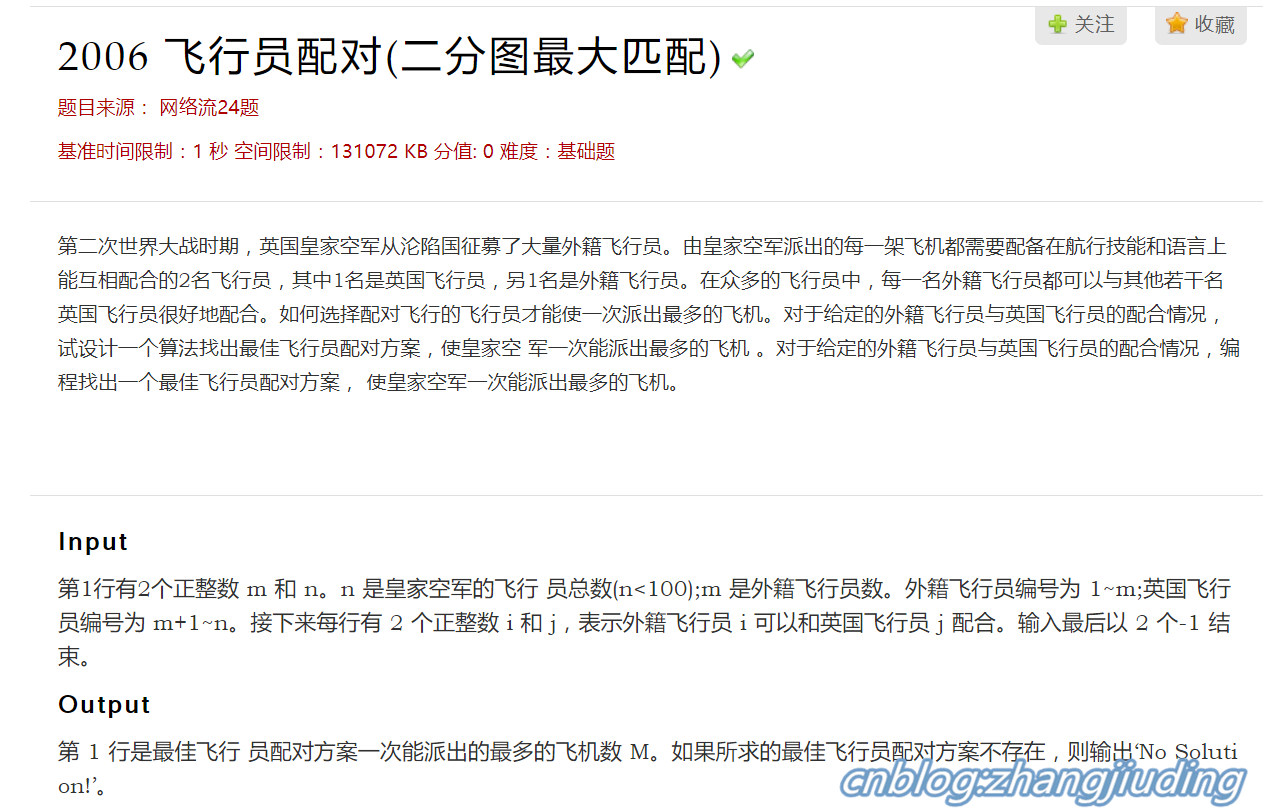
题目已经说了是最大二分匹配题，

查了一下最大二分匹配题有两种解法，

匈牙利算法和网络流。

看了一下觉得匈牙利算法更好理解，

然后我照着小红书模板打了一遍就过了。

 

 

匈牙利算法：先试着把没用过的左边的点和没用过的右边的点连起来，

　　　　　　如果遇到一个点已经连过就试着把原来的拆掉 把现在这条线连起来看能不能多连上一条线。

 

总结来说就是试和拆，试的过程很简单，拆的过程由于使用递归写的，很复杂。很难讲清楚，只能看代码自己理会。

 

代码（有注释）：

#include <bits\stdc++.h>
using namespace std;
typedef long long ll;

//输入：
const  int MAXN = 555; // 数组长度
int n = 200; //n表示左侧的点数
vector <int> g[MAXN];  // 表示与左边点i相连的右边点

//输出：
int from[MAXN];//表示最大匹配中与左边点i相连的边
int tot;  // 二分图最大匹配数


bool use[MAXN]; // 左边点的使用标记


//匈牙利算法 模板题 ，match和hungary见小红书ACM国际大学生程序设计竞赛 算法与实现
bool match(int x){
    for(int i = 0;i < g[x].size(); ++i){
        if(!use[g[x][i]]){
            use[g[x][i]] = true;
            if(from[g[x][i]] == -1 || match(from[g[x][i]])){
                from[g[x][i]] = x;
                return true;
            }
        }
    }
    return false;
}

int hungary(){
    tot = 0;
    memset(from,255,sizeof(from));
    for(int i = 1;i <= n; i++){
        memset(use,0,sizeof(use));
        if(match(i)) ++tot;
    }
    return tot;
}

int main() {
    int m;
    cin >> n >> m;
    int k1,k2;
    cin >> k1 >> k2;
    while(k1 != -1||k2 != -1){
        g[k1].push_back(k2-n);
        cin >> k1 >> k2;
    };
    cout << hungary() << endl;
    return 0;
}

 

 

模板：http://www.cnblogs.com/zhangjiuding/p/7538876.html