旋转卡壳与计算几何应用篇
旋转卡壳
这种东西,你只要理解做法就行了,因为这种东西十分的玄。
题目描述
【题意】
给出n个点的坐标,求最远两点间的距离。
【输入格式】
第一行一个整数n(2 ≤ n ≤ 50000)。
下来n行,每行两个实数x和y表示点坐标(x,y<=|10^6|)。
【输出格式】
一行一个实数,表示最远两点间的距离的平方(保留2位小数)。
【样例输入】
5
0 0
0 5
5 0
5 5
2 0
【样例输出】
50.00
凸包
我们首先可以知道最长的距离肯定在凸包上,如果不在,你可以连线最近的两个在凸包上的点,总有一条是大于这个线段的。
旋转!跳跃!
那么,在凸包上我们还能怎么做?O(n^2)
那么这就很伤了呀。
但是还是有大佬发明了一个\(O(n)\)的算法。
我们现在准备两条平行线,卡住这个凸多边形。
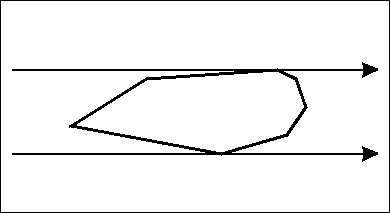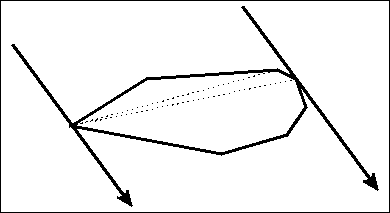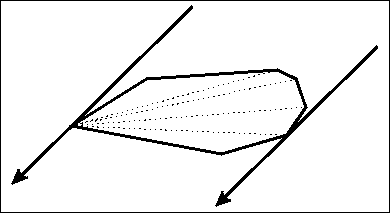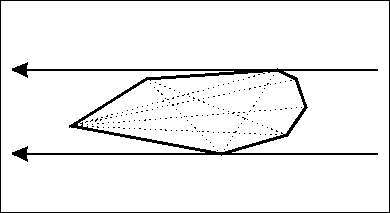
来源于https://jvruo.com/archives/79/
当然,卡住的情况有三种:
- 点对点。
- 点对边
- 边对边
由于点对点比较难,后面旋转的时候会旋转成点对边,而且边对边可以拆成两个点对边,所以我们只讨论点对边的情况,也就是这种情况:

但是如何求对踵点?选一条边,存在一个点使得构成的三角形面积最大的就是对踵点,同时也就是点对边。
通过自己感性的理解以及加以画图,应该可以理解为什么是对踵点才是最长的了。
而且我们会发现,我们逆时针模拟的话,对踵点也是绕着凸包逆时针旋转。
有人证明过,对踵点对数量小于\(\frac{3n}{2}\)
错误示范
为什么模拟点对边可以模拟出所有的对踵点。
举一个简单的例子:

你会发现以\(AF,AE\)为边的话,\(AB\)这对对踵点无法找到,这就很气人了,我也以为旋转卡壳是错的。
但是调试发现\(BD\)就会以\(A\)为对踵点了。
自己画了几个图发现,对踵点至少会被点到一次,最多被点到四次。
代码
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#define N 111000
using namespace std;
double eps=1e-10;
struct dian{double x,y;}aa[N],sta[N];int n,top;
inline double mu(dian x1,dian x2,dian y){return (x1.x-y.x)*(x2.y-y.y)-(x2.x-y.x)*(x1.y-y.y);}//叉积
inline double dis(dian x,dian y){return (x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y);}//距离,不用开根,这题开根会掉精
inline bool cmp(dian x,dian y)//排序
{
double tt=mu(x,y,aa[1]);
if(tt>eps)return true;
else if(fabs(tt)<=eps && dis(aa[1],x)<dis(aa[1],y))return true;
return false;
}
void tubao()//凸包
{
sort(aa+2,aa+n+1,cmp);
top=2;sta[1]=aa[1];sta[2]=aa[2];
for(int i=3;i<=n;i++)
{
while(top>1 && mu(sta[top],aa[i],sta[top-1])<=0)top--;
sta[++top]=aa[i];
}
}
inline double mymax(double x,double y){return x>y?x:y;}
void ka()
{
double ans=0;
sta[++top]=sta[1];/*收尾相连*/int now=2;//特判点数1与2的情况
for(int i=1;i<top;i++)
{
while(mu(sta[i+1],sta[now+1],sta[i])>mu(sta[i+1],sta[now],sta[i]))//叉积求面积,这里需要处理好旋转方向,保证面积大于0
{
now++;if(now==top)now=1;
}
ans=mymax(ans,dis(sta[now],sta[i]));
}
printf("%.2lf\n",ans);//dis没开根
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%lf%lf",&aa[i].x,&aa[i].y);
if(aa[i].x<aa[1].x || (aa[i].x==aa[1].x && aa[i].y<aa[1].y)){dian zjj=aa[1];aa[1]=aa[i];aa[i]=zjj;}
}
tubao();//凸包
ka();//旋转卡壳
return 0;
}
一些练习
1
题目描述
【题目描述】
给定平面上N个点,你需要计算以其中4个点为顶点的正方形的个数。注意这里的正方形边不一定需要和坐标轴平行。
【输入文件】
第一行一个数N,以下N个点的坐标。
【输出文件】
一个数正方形的个数。
【样例输入】
7
0 0
0 1
1 0
1 1
1 2
2 1
2 2
【样例输出】
3
【数据规模】
对于20%的数据,满足1≤N≤20;
对于l00%的数据,满足1≤N≤500,-50≤X[i],Y[i]≤50,点不会重叠。
暴力枚举两个点,然后一直暴力一直爽。
#include<cstdio>
#include<cstring>
using namespace std;
int a[610][2],n,ans;
bool bk[610][610];
void work(int x,int y)
{
int xx=(a[y][0]-a[x][0]),yy=(a[y][1]-a[x][1]);
int x1=a[x][0]-yy,y1=a[x][1]+xx,x2=a[y][0]-yy,y2=a[y][1]+xx;
if(bk[x1][y1] && bk[x2][y2])ans++;
x1=a[x][0]+yy,y1=a[x][1]-xx,x2=a[y][0]+yy,y2=a[y][1]-xx;//暴力算出两个三角形,bool矩阵暴力判
if(bk[x1][y1] && bk[x2][y2])ans++;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int x,y;scanf("%d%d",&x,&y);x+=150;y+=150;
a[i][0]=x;a[i][1]=y;bk[x][y]=true;
}
for(int i=1;i<=n;i++)
{
for(int j=i+1;j<=n;j++)work(i,j);
}
printf("%d\n",ans/4);//每个矩阵重复算四次
return 0;
}
2
翻译:
给你一堆构成凸包的点,然后以原点为基准,逆时针输出所有的点。
无三点共线,无其他点在x,y轴。
暴力一直爽,一直暴力一直爽。
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
double eps=1e-8;
struct dian{double x,y;}a[100];
double pd(dian x1,dian x2,dian y){return (x1.x-y.x)*(x2.y-y.y)-(x2.x-y.x)*(x1.y-y.y);}
bool cmp(dian x,dian y)
{
if(pd(x,y,a[1])>eps)return true;
return false;
}
int n;
int main()
{
// freopen("sb.in","r",stdin);
n=1;
while(scanf("%lf%lf",&a[n].x,&a[n].y)!=EOF)
{
if(a[n].x<a[1].x || (fabs(a[n].x-a[1].x)<=eps && a[n].y<a[1].y)){dian z=a[n];a[n]=a[1];a[1]=z;}
n++;
}
n--;
sort(a+2,a+n+1,cmp);//类似凸包的排序
for(int i=1;i<=n;i++)
{
if(a[i].x==0 && a[i].y==0)//找到原点
{
for(int j=i;j<=n;j++)printf("(%.0lf,%.0lf)\n",a[j].x,a[j].y);
for(int j=1;j<i;j++)printf("(%.0lf,%.0lf)\n",a[j].x,a[j].y);
break;
}
}
return 0;
}
3
大概意思就是说给你一些半径一样的圆,求类似凸包的周长。

那么我们容易看出其实就是凸包的周长加上一个圆周。
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
double eps=1e-8,pai=3.1415926535897932;
struct dian{double x,y;}a[1100],sta[1100];int n,len;double l;
inline double mu(dian x,dian y,dian z){return (x.x-z.x)*(y.y-z.y)-(y.x-z.x)*(x.y-z.y);}
inline double dis(dian x,dian y){return sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y));}
inline bool cmp(dian x,dian y)
{
double tt=mu(x,y,a[1]);
if(tt>eps)return true;
else if(fabs(tt)<=eps && dis(x,a[1])-dis(y,a[1])<-eps)return true;
return false;
}
int main()
{
scanf("%d%lf",&n,&l);
for(int i=1;i<=n;i++)
{
scanf("%lf%lf",&a[i].x,&a[i].y);
if(a[i].x-a[1].x<-eps || (fabs(a[i].x-a[1].x)<=eps && a[i].y-a[1].y<-eps)){dian z=a[1];a[1]=a[i];a[i]=z;}
}
sort(a+2,a+n+1,cmp);
len=2;sta[1]=a[1];sta[2]=a[2];
for(int i=3;i<=n;i++)
{
while(len>1 && mu(a[i],sta[len],sta[len-1])>=-eps)len--;
sta[++len]=a[i];
}
sta[len+1]=sta[1];
double ans=0.0;
for(int i=1;i<=len;i++)ans+=dis(sta[i],sta[i+1]);
ans+=pai*2*l;//圆周
printf("%.0lf\n",ans);
return 0;
}
4
逆时针输出点,其实很弱智,但是我们可以发现不管作那个点为基准点做逆时针排序,得出的逆时针顺序都一样。
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
double eps=1e-8;
struct dian{double x,y;}a[100];
double pd(dian x1,dian x2,dian y){return (x1.x-y.x)*(x2.y-y.y)-(x2.x-y.x)*(x1.y-y.y);}
bool cmp(dian x,dian y)
{
if(pd(x,y,a[1])>eps)return true;//无共线情况
return false;
}
int n;
int main()
{
n++;
while(scanf("%lf%lf",&a[n].x,&a[n].y)!=EOF)
{
if(fabs(a[n].x)<=eps && fabs(a[n].y)<=eps){dian z=a[n];a[n]=a[1];a[1]=z;}
n++;
}
n--;
sort(a+2,a+n+1,cmp);
for(int i=1;i<=n;i++)printf("(%.0lf,%.0lf)\n",a[i].x,a[i].y);
return 0;
}
5
判断是否是稳定凸包。
也就是每条边都至少有三个点。(特判直线情况)
用类似凸包的方法排序(虽然不是很需要,可以把凸包去掉,并改改代码,但是懒得改了,当时),但是应当特判最后一条边。
一个数据:
1
7
0 0
1 0
2 0
2 1
2 2
1 2
0 2
NO
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
using namespace std;
struct dian
{
double x,y;
}a[1100],sta[1100];int n;double eps=1e-7;
double mu(dian x,dian y,dian z){return (x.x-z.x)*(y.y-z.y)-(y.x-z.x)*(x.y-z.y);}
double dis(dian x,dian y){return sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y));}
bool cmp(dian x,dian y)
{
double tt=mu(x,y,a[1]);
if(tt>eps)return true;
else if(fabs(tt)<=eps && dis(a[1],x)-dis(a[1],y)<=eps)return true;
return false;
}
int main()
{
int T;scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%lf%lf",&a[i].x,&a[i].y);
if(a[i].x-a[1].x<-eps || (fabs(a[i].x-a[1].x)<=eps && a[i].y-a[1].y<-eps)){dian z=a[1];a[1]=a[i];a[i]=z;}
}
sort(a+2,a+n+1,cmp);
int top=2;sta[1]=a[1];sta[2]=a[2];
for(int i=3;i<=n;i++)
{
while(top>1 && mu(a[i],sta[top],sta[top-1])>eps)top--;
sta[++top]=a[i];
}
//凸包判排序
if((n-1)>1 && fabs(mu(a[n-1],sta[top],sta[1]))<=eps)//最后一条边有点与top共线
{
dian now=sta[top];
for(int i=top;i>1;i--)
{
if(fabs(mu(sta[i],now,sta[1]))<=eps)top--;
else break;
}//去掉最后一条边,重复点的情况。
sta[++top]=now;//保留一个点。
if(top<=2)//一条直线
{
printf("NO\n");
continue;
}
bool bk=false;
for(int i=3;i<=top;i++)
{
if(fabs(mu(sta[i-2],sta[i-1],sta[i]))<=eps)bk=true;
else
{
if(bk==true)bk=false;
else break;
}
}
if(bk==false)printf("NO\n");
else printf("YES\n");
}
else printf("NO\n");
}
return 0;
}
6
判断情况。
分别用斜率与两点式(\(ax+by+c=0\),求的公式在代码中有)做了。
斜率版:
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
using namespace std;
struct dian
{
double x,y;
dian(double xx=0.0,double yy=0.0){x=xx;y=yy;}
}xx1,yy1,xx2,yy2;double eps=1e-7;
dian pd(dian x,dian y)
{
dian z;z.x=(x.y-y.y)/(x.x-y.x);//斜率
z.y=x.y-x.x*z.x;
return z;
}
double mu(dian x,dian y,dian z){return (x.x-z.x)*(y.y-z.y)-(y.x-z.x)*(x.y-z.y);}
dian jd()
{
double t1=mu(yy2,xx1,xx2),t2=mu(yy2,yy1,xx2);
return dian((t1*yy1.x-t2*xx1.x)/(t1-t2),(t1*yy1.y-t2*xx1.y)/(t1-t2));
}
void solve()
{
dian q=pd(xx1,yy1),p=pd(xx2,yy2);
if(xx1.x==yy1.x)//特判y=0的直线
{
if(xx2.x==yy2.x)
{
if(xx1.x==xx2.x)printf("LINE\n");
else printf("NONE\n");
}
else printf("POINT %.2lf %.2lf\n",xx1.x,xx1.x*p.x+p.y);
return ;
}
if(fabs(q.x-p.x)<=eps)
{
if(fabs(q.y-p.y)<=eps)printf("LINE\n");
else printf("NONE\n");
}
else
{
dian z=jd();
printf("POINT %.2lf %.2lf\n",z.x,z.y);
}
}
int main()
{
// freopen("sb.out","w",stdout);
printf("INTERSECTING LINES OUTPUT\n");
int n;scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&xx1.x,&xx1.y,&yy1.x,&yy1.y,&xx2.x,&xx2.y,&yy2.x,&yy2.y);
solve();
}
printf("END OF OUTPUT\n");
return 0;
}
两点式:
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
using namespace std;
struct dian
{
double x,y;
dian(double xx=0.0,double yy=0.0){x=xx;y=yy;}
}xx1,yy1,xx2,yy2;double eps=1e-6;
struct node{double x,y,z;};
node pd(dian x,dian y)//求两点式
{
//(x-x1)/(x2-x1)=(y-y1)/(y2-y1)相似三角形可以求出此式子
//(x-x1)(y2-y1)=(y-y1)(x2-x1)相似三角形
//(y2-y1)x+(x1-x2)y+(x1y1-x1y2+y1x2-x1y1)
//(y2-y1)x+(x1-x2)y+(y1x2-x1y2)
node z;z.x=(y.y-x.y);z.y=(x.x-y.x);z.z=(x.y*y.x-x.x*y.y);
return z;
}
double mu(dian x,dian y,dian z){return (x.x-z.x)*(y.y-z.y)-(y.x-z.x)*(x.y-z.y);}
dian jd()
{
double t1=mu(yy2,xx1,xx2),t2=mu(yy2,yy1,xx2);
return dian((t1*yy1.x-t2*xx1.x)/(t1-t2),(t1*yy1.y-t2*xx1.y)/(t1-t2));
}
void solve()
{
node q=pd(xx1,yy1),p=pd(xx2,yy2);
if(fabs(q.x*p.y-q.y*p.x)<=eps)
{
if(fabs(q.z*p.y-p.z*q.y)<=eps && fabs(q.z*p.x-p.z*q.x)<=eps)printf("LINE\n");
else printf("NONE\n");
}
else
{
dian z=jd();
printf("POINT %.2lf %.2lf\n",z.x,z.y);
}
}
int main()
{
// freopen("sb.out","w",stdout);
printf("INTERSECTING LINES OUTPUT\n");
int n;scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&xx1.x,&xx1.y,&yy1.x,&yy1.y,&xx2.x,&xx2.y,&yy2.x,&yy2.y);
solve();
}
printf("END OF OUTPUT\n");
return 0;
}
7
//双倍经验
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
using namespace std;
double eps=1e-8;
struct dian{double x,y;};
struct line{dian x,y;}a[110000];
double mu(dian x,dian y,dian z){return (x.x-z.x)*(y.y-z.y)-(y.x-z.x)*(x.y-z.y);}
double mymin(double x,double y){return x<y?x:y;}
double mymax(double x,double y){return x>y?x:y;}
bool pd(line x,dian y){return (y.x>=mymin(x.x.x,x.y.x) && y.x<=mymax(x.x.x,x.y.x) && y.y>=mymin(x.x.y,x.y.y) && y.y<=mymax(x.x.y,x.y.y));}
bool solve(line x,line y)
{
if(mu(y.y,x.x,y.x)*mu(y.y,x.y,y.x)<-eps && mu(x.y,y.x,x.x)*mu(x.y,y.y,x.x)<-eps)return true;
if((fabs(mu(x.x,y.x,y.y))<=eps && pd(y,x.x)==true) ||
(fabs(mu(x.y,y.x,y.y))<=eps && pd(y,x.y)==true) ||
(fabs(mu(y.x,x.x,x.y))<=eps && pd(x,y.x)==true) ||
(fabs(mu(y.y,x.x,x.y))<=eps && pd(x,y.y)==true))return true;
return false;
}
int n,ans[110000];
int main()
{
while(scanf("%d",&n)!=EOF)
{
if(n==0)break;
for(int i=1;i<=n;i++)scanf("%lf%lf%lf%lf",&a[i].x.x,&a[i].x.y,&a[i].y.x,&a[i].y.y);
ans[0]=0;
for(int i=1;i<=n;i++)
{
bool bk=false;
for(int j=i+1;j<=n;j++)
{
if(solve(a[i],a[j])==true){bk=true;break;}
}
if(bk==false)ans[++ans[0]]=i;
}
printf("Top sticks:");
for(int i=1;i<ans[0];i++)printf(" %d,",ans[i]);
printf(" %d.\n",ans[ans[0]]);
}
return 0;
}
8
逆时针的半平面交双倍经验。
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#define N 110
using namespace std;
double eps=1e-8;
int n;
struct dian
{
double x,y;
dian(double xx=0,double yy=0){x=xx;y=yy;}
};
struct line
{
dian x,y;
double agr;
void made(){agr=atan2(y.y-x.y,y.x-x.x);}
}a[N],sta[N];int head,tail;
inline double mu(dian x,dian y,dian z){return (x.x-z.x)*(y.y-z.y)-(y.x-z.x)*(x.y-z.y);}
inline dian jd(line x,line y)
{
double t1=mu(y.x,x.x,y.y),t2=mu(y.x,x.y,y.y);
return dian((t1*x.y.x-t2*x.x.x)/(t1-t2),(t1*x.y.y-t2*x.x.y)/(t1-t2));
}
inline bool safe(line x,dian y){return mu(y,x.y,x.x)<=eps;}
inline bool cmp(line x,line y)
{
if(x.agr-y.agr<-eps)return true;
else if(fabs(x.agr-y.agr)<=eps && safe(y,x.x)==true)return true;
return false;
}
inline bool bpm()
{
sort(a+1,a+n+1,cmp);
int tp=1;for(int i=2;i<=n;i++)if(fabs(a[i].agr-a[i-1].agr)>eps)a[++tp]=a[i];
n=tp;
head=1;tail=2;sta[1]=a[1];sta[2]=a[2];
for(int i=3;i<=n;i++)
{
while(head<tail && safe(a[i],jd(sta[tail],sta[tail-1]))==false)tail--;
while(head<tail && safe(a[i],jd(sta[head],sta[head+1]))==false)head++;
sta[++tail]=a[i];
}
while(head<tail && safe(sta[head],jd(sta[tail],sta[tail-1]))==false)tail--;
if(tail-head+1<=2)return false;
return true;
}
int main()
{
while(scanf("%d",&n)!=EOF)
{
if(n==0)break;
for(int i=1;i<=n;i++)
{
double x,y;scanf("%lf%lf",&x,&y);
a[i-1].y.x=a[i].x.x=x;a[i-1].y.y=a[i].x.y=y;
a[i-1].made();
}
a[n].y.x=a[1].x.x;a[n].y.y=a[1].x.y;a[n].made();
if(bpm())printf("1\n");
else printf("0\n");
}
return 0;
}
9
双倍经验,变成顺时针。
//非凸多边形不能用叉积判顺逆
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#define N 210
using namespace std;
double eps=1e-8;
int n;
struct dian
{
double x,y;
dian(double xx=0,double yy=0){x=xx;y=yy;}
};
struct line
{
dian x,y;
double agr;
void made(){agr=atan2(y.y-x.y,y.x-x.x);}
}a[N],sta[N];int head,tail;
inline double mu(dian x,dian y,dian z){return (x.x-z.x)*(y.y-z.y)-(y.x-z.x)*(x.y-z.y);}
inline dian jd(line x,line y)
{
double t1=mu(y.x,x.x,y.y),t2=mu(y.x,x.y,y.y);
return dian((t1*x.y.x-t2*x.x.x)/(t1-t2),(t1*x.y.y-t2*x.x.y)/(t1-t2));
}
inline bool safe(line x,dian y){return mu(y,x.y,x.x)<=eps;}
inline bool cmp(line x,line y)
{
if(x.agr-y.agr<-eps)return true;
else if(fabs(x.agr-y.agr)<=eps && safe(y,x.x)==true)return true;
return false;
}
inline bool bpm()
{
sort(a+1,a+n+1,cmp);
int tp=1;for(int i=2;i<=n;i++)if(fabs(a[i].agr-a[i-1].agr)>eps)a[++tp]=a[i];
n=tp;
head=1;tail=2;sta[1]=a[1];sta[2]=a[2];
for(int i=3;i<=n;i++)
{
while(head<tail && safe(a[i],jd(sta[tail],sta[tail-1]))==false)tail--;
while(head<tail && safe(a[i],jd(sta[head],sta[head+1]))==false)head++;
sta[++tail]=a[i];
}
while(head<tail && safe(sta[head],jd(sta[tail],sta[tail-1]))==false)tail--;
if(tail-head+1<=2)return false;
return true;
}
int main()
{
int T;scanf("%d",&T);
for(int i=1;i<=T;i++)
{
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%lf%lf",&a[i].x.x,&a[i].x.y);
for(int i=n-1;i>=1;i--)a[i+1].y=a[i].x,a[i+1].made();
a[1].y=a[n].x;a[1].made();
if(bpm())printf("YES\n");
else printf("NO\n");
}
return 0;
}
10
多次双倍经验,顺时针。
//非凸多边形不能用叉积判顺逆
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#define N 210
using namespace std;
double eps=1e-8;
int n;
struct dian
{
double x,y;
dian(double xx=0,double yy=0){x=xx;y=yy;}
};
struct line
{
dian x,y;
double agr;
void made(){agr=atan2(y.y-x.y,y.x-x.x);}
}a[N],sta[N];int head,tail;
inline double mu(dian x,dian y,dian z){return (x.x-z.x)*(y.y-z.y)-(y.x-z.x)*(x.y-z.y);}
inline dian jd(line x,line y)
{
double t1=mu(y.x,x.x,y.y),t2=mu(y.x,x.y,y.y);
return dian((t1*x.y.x-t2*x.x.x)/(t1-t2),(t1*x.y.y-t2*x.x.y)/(t1-t2));
}
inline bool safe(line x,dian y){return mu(y,x.y,x.x)<=eps;}
inline bool cmp(line x,line y)
{
if(x.agr-y.agr<-eps)return true;
else if(fabs(x.agr-y.agr)<=eps && safe(y,x.x)==true)return true;
return false;
}
inline bool bpm()
{
sort(a+1,a+n+1,cmp);
int tp=1;for(int i=2;i<=n;i++)if(fabs(a[i].agr-a[i-1].agr)>eps)a[++tp]=a[i];
n=tp;
head=1;tail=2;sta[1]=a[1];sta[2]=a[2];
for(int i=3;i<=n;i++)
{
while(head<tail && safe(a[i],jd(sta[tail],sta[tail-1]))==false)tail--;
while(head<tail && safe(a[i],jd(sta[head],sta[head+1]))==false)head++;
sta[++tail]=a[i];
}
while(head<tail && safe(sta[head],jd(sta[tail],sta[tail-1]))==false)tail--;
if(tail-head+1<=2)return false;
return true;
}
int main()
{
int T=0;
while(scanf("%d",&n)!=EOF)
{
if(n==0)break;
T++;printf("Floor #%d\n",T);
for(int i=1;i<=n;i++)scanf("%lf%lf",&a[i].x.x,&a[i].x.y);
for(int i=n-1;i>=1;i--)a[i+1].y=a[i].x,a[i+1].made();
a[1].y=a[n].x;a[1].made();
if(bpm())printf("Surveillance is possible.\n\n");
else printf("Surveillance is impossible.\n\n");
}
return 0;
}
11
顺时针,在多求个面积。。。
//非凸多边形不能用叉积判顺逆
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#define N 2110
using namespace std;
double eps=1e-8;
int n;
struct dian
{
double x,y;
dian(double xx=0,double yy=0){x=xx;y=yy;}
}pl[N];
struct line
{
dian x,y;
double agr;
void made(){agr=atan2(y.y-x.y,y.x-x.x);}
}a[N],sta[N];int head,tail;
inline double mu(dian x,dian y,dian z){return (x.x-z.x)*(y.y-z.y)-(y.x-z.x)*(x.y-z.y);}
inline dian jd(line x,line y)
{
double t1=mu(y.x,x.x,y.y),t2=mu(y.x,x.y,y.y);
return dian((t1*x.y.x-t2*x.x.x)/(t1-t2),(t1*x.y.y-t2*x.x.y)/(t1-t2));
}
inline bool safe(line x,dian y){return mu(y,x.y,x.x)<=eps;}
inline bool cmp(line x,line y)
{
if(x.agr-y.agr<-eps)return true;
else if(fabs(x.agr-y.agr)<=eps && safe(y,x.x)==true)return true;
return false;
}
inline void bpm()
{
sort(a+1,a+n+1,cmp);
int tp=1;for(int i=2;i<=n;i++)if(fabs(a[i].agr-a[i-1].agr)>eps)a[++tp]=a[i];
n=tp;
head=1;tail=2;sta[1]=a[1];sta[2]=a[2];
for(int i=3;i<=n;i++)
{
while(head<tail && safe(a[i],jd(sta[tail],sta[tail-1]))==false)tail--;
while(head<tail && safe(a[i],jd(sta[head],sta[head+1]))==false)head++;
sta[++tail]=a[i];
}
while(head<tail && safe(sta[head],jd(sta[tail],sta[tail-1]))==false)tail--;
if(tail-head+1<=2)
{
printf("0.00\n");
return ;
}
double ans=0;int len=0;
for(int i=head;i<tail;i++)pl[++len]=jd(sta[i],sta[i+1]);pl[++len]=jd(sta[head],sta[tail]);
for(int i=3;i<=len;i++)ans+=mu(pl[i-1],pl[i],pl[1]);
printf("%.2lf\n",fabs(ans/2));
}
int main()
{
int T;scanf("%d",&T);
for(int i=1;i<=T;i++)
{
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%lf%lf",&a[i].x.x,&a[i].x.y);
for(int i=n-1;i>=1;i--)a[i+1].y=a[i].x,a[i+1].made();
a[1].y=a[n].x;a[1].made();
bpm();
}
return 0;
}

