2017-2018-1 20162304 实验二 树
2017-2018-1 20162304 实验二 树
树-1-实现二叉树
- 具体实现思路见代码中的注释
public boolean contains(T target) { //该方法就是需要先想好有三种情况,然后分别写就行
if(target == null)
return false;
if ((root.find(target))!=null)
return true;
else
return false;
}
public LinkedBinaryTree<T> getRight() { //这个方法我直接根据getLeft方法的思路就可以得到啦。
if (root == null)
throw new EmptyCollectionException("Get left operation "
+ "failed. The tree is empty.");
LinkedBinaryTree<T> result = new LinkedBinaryTree<T>();
result.root = root.getRight();
return result;
}
public boolean isEmpty() { //直接返回根值是否为空即可
return root == null;
}
public String toString() { //这个方法的思路就是先遍历再打印
String a = levelorder().toString();
return a;
}
测试代码
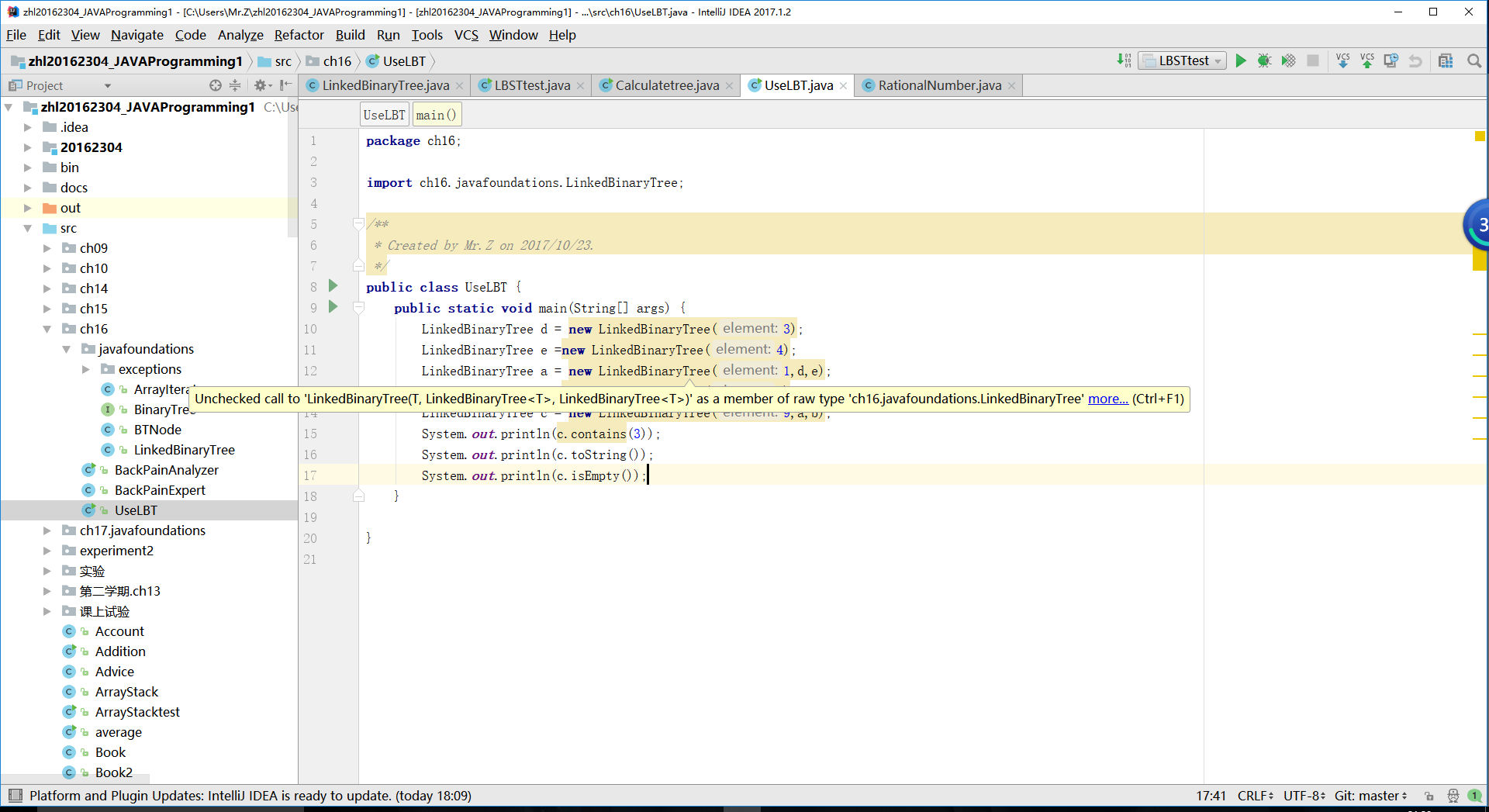
树-2-中序先序序列构造二叉树
实验代码
public class TreeReBuild {
public static BTNode reConstructBinaryTree1(char[] pre, char[] in) {
if (pre.length == 0 || in.length == 0 || pre.length != in.length) {
return null;
}
BTNode root = new BTNode(pre[0]);
int i = 0;
while (in[i] != pre[0]) {
i++;
}
char[] preLeft = new char[i];
char[] inLeft = new char[i];
char[] preRight = new char[pre.length - i - 1];
char[] inRight = new char[in.length - i - 1];
for (int j = 0; j < in.length; j++) {
if (j < i) {
preLeft[j] = pre[j + 1];
inLeft[j] = in[j];
} else if (j > i) {
preRight[j - i - 1] = pre[j];
inRight[j - i - 1] = in[j];
}
}
root.setLeft(reConstructBinaryTree1(preLeft,inLeft));
root.setRight( reConstructBinaryTree1(preRight,inRight));
return root;
}
public static void last(BTNode tr) {
if (tr == null) {
return;
}
last(tr.getLeft());
last(tr.getRight());
System.out.print(tr.count() + " ");
}
public static void main(String[] args) {
char[] a = "ABDHIEJMNCFGKL".toCharArray();
char[] b = "HDIBEMJNAFCKGL".toCharArray();
BTNode root = reConstructBinaryTree1(a, b);
LinkedBinaryTree T = new LinkedBinaryTree(root);
System.out.println(T.toString());
}
}
代码结果
树-3-决策树
问题及答案设计

结果展示

树-4-表达式树

实验结果
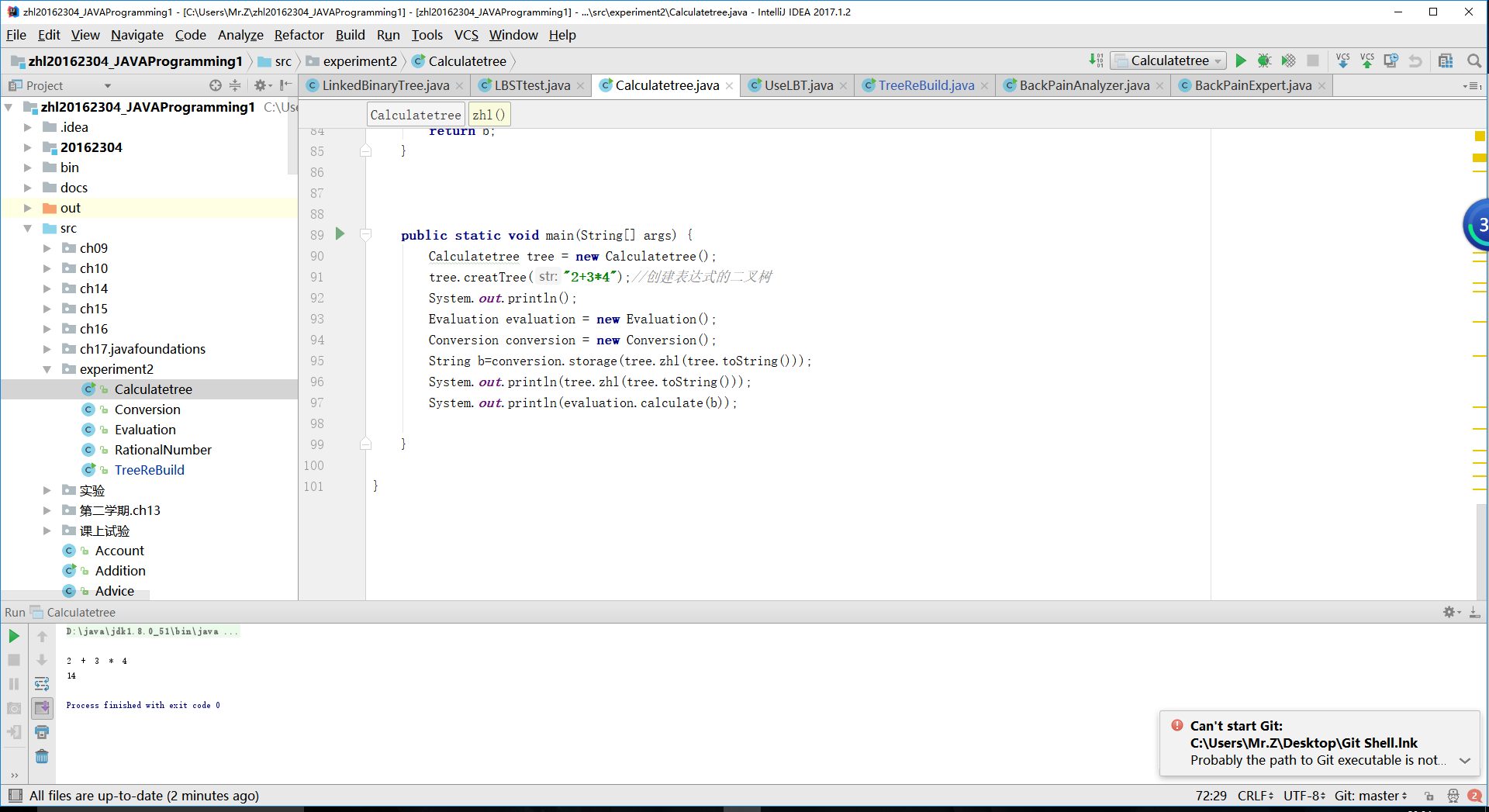
实验中遇到的问题
- 在我完成用二叉树来表示表达式树这个操作后,发现自己生成的表达式没法通过上学期我们编写的四则运算代码计算,然后通过和同学的讨论,对代码的分析,我们发现是因为格式不对,导致程序无法识别。之后我们对输出结果的格式进行了一个修改,代码如下。
public String zhl(String a){
String b = "";
for (int i = 0; i<a.length(); i++) {
switch (a.charAt(i)) {
case ',':
b += "";
break;
case '[':
b += "";
break;
case ']':
b += "";
break;
default:
b += a.charAt(i);
}
}
return b;
}
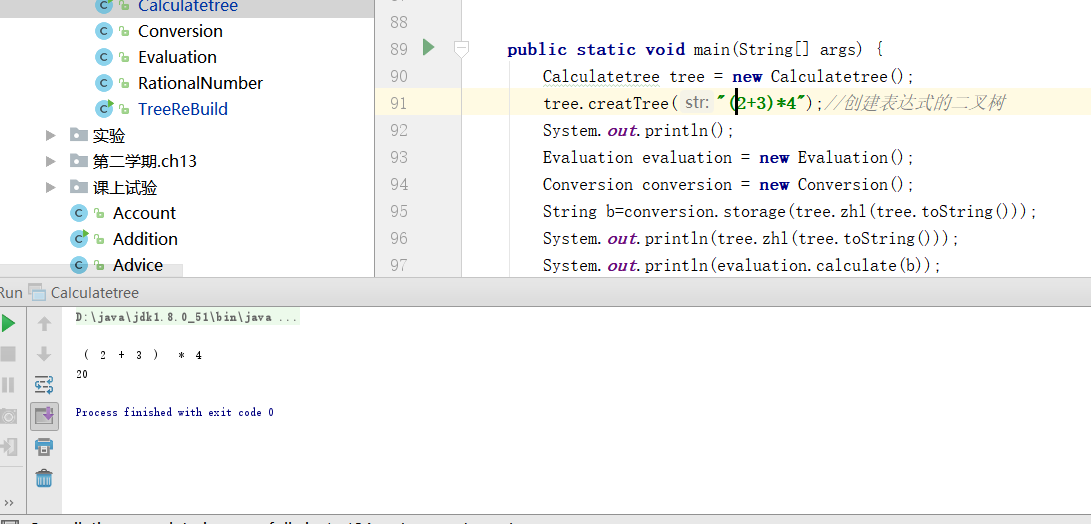
经过这个处理,我们便完成了对树进行计算得到结果的目的。
实验结果
树-5-二叉查找树

实验思路
- 根据对书上排序树的观察我发现最大的数字在树的最右边,最小的在树的最左边,因此便可以得到代码。
代码实现
public T findMin() {
BTNode<T> zhl = root;
while (zhl.getLeft()!=null){
zhl = zhl.getLeft();
}
return zhl.getElement();
}
@Override
public T findMax() {
BTNode<T> a = root;
while (a.getRight()!=null){
a = a.getRight();
}
return a.getElement();
}
实验成果
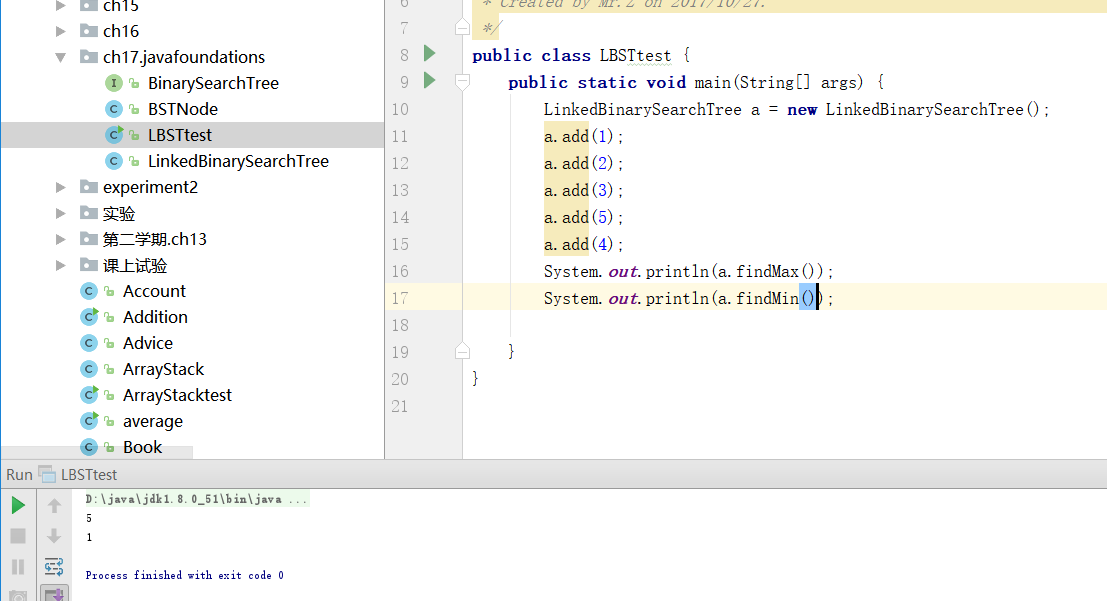
树-6-红黑树分析

实验思路
- 红黑树定义:红黑树又称红-黑二叉树,它首先是一颗二叉树,它具体二叉树所有的特性。同时红黑树更是一颗自平衡的排序二叉树(平衡二叉树的一种实现方式)。

- 红黑树最重要的5点规则:
1、每个结点都只能是红色或者黑色中的一种。
2、根结点是黑色的。
3、每个叶结点(NIL节点,空节点)是黑色的。
4、如果一个结点是红的,则它两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。
5、从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。
代码分析
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
- 这个方法是一个赋值的方法
public int size() {
if (fromStart && toEnd)
return m.size();
if (size == -1 || sizeModCount != m.modCount) {
sizeModCount = m.modCount;
size = 0;
Iterator<?> i = iterator();
while (i.hasNext()) {
size++;
i.next();
}
}
return size;
}
· 这段代码,是通过hsanext来返回size的大小。
实验感想
总的来说,感觉还是不怎么会源码分析,接下来会努力提高。




