word2vec

统计语言模型

问题：如何计算一段文本序列出现的概率？

建模：句子S由T个词组成，$S=w_1,w_2,\cdots,w_T$。则句子出现的概率

$$p(S)=\prod_{i=1}^T{p(w_i|context_{w_i})}$$

$context_{w_i}$表示词$w_i$的上下文环境，统计语言模型作了2个简化：

1. $context_{w_i}$就是一些词的集合，与词出现的顺序无关，即$context_{w_i}=\{{w_1,w_2,\cdots,w_{i-1},w_{i+1},\cdots,w_T}\}$。
2. 进一步简化，只有前后$n-1$个词对$w_i$有影响，即$context_{w_i}=\{w_{i-n+1},\cdots,w_{i-1},w_{i+1},\cdots,w_{i+n-1}\}$。或者更简单地，只有前面$n-1$个词对$w_i$有影响，即$context_{w_i}=\{w_{i-n+1},\cdots,w_{i-1}\}$，这就是所谓的N-gram模型。1-gram表示每个词都是相互独立的，2-gram表示每个词只受它前面一个词的影响。

N-gram模型有3个弊端：

1. 零频问题对N-gram模型的效果影响很大，所以出现了很多平滑算法。
2. N不能很大，否则零频问题会更严重，运算量会爆炸。
3. 它将词看作孤立的单元，没有考虑词之间内在的联系。下面会详细解释这一点。

词义的分布式表达(Distributed Representation)

比如语料库有大量这样的句子“我喜欢养宠物猫”、“我喜欢养宠物狗”、“猫整天在卧室里走动”。现在来了个新句子“狗整天在卧室里走动”，让你判断这句话出现的概率，根据统计语言模型会得出这句话的概率很低，因为在语料库中“狗”很少出现在“整天在卧室里走动”这样的语境中。这个问题怎么解决？可以采用词义的分布式表达，假设所有词的词义构成一个N维的空间，一个词的词义在各个维度上都有一个分量，即一个词可以用一个N维向量来表示。最简单的做法就共现矩阵。假设总共有N个词，那词义空间就是N维，计算出每个词与其他词在语料库中共现的次数，作为这个词的向量表达。这样一来，因为“猫”和“狗”跟{我，喜欢，养，宠物}这些词的共现度都很高，所以“猫”和“狗”的向量表达就很接近，我们就可以认为“猫”和“狗”是近义词。又因为“猫整天在卧室里走动”经常在语料库中出现，所以我们可以认为“狗整天在卧室里走动”这句话的概率也应该比较高。

共现矩阵仍然存在稀疏性和维度灾难的问题，所以才有了LSI和PCA等降维的方法，它都是基于奇异值分解的，即把高维的稀疏矩阵分解为两个低维矩阵的乘积。

基于神经网络的语言模型

 基于神经网络的语言模型属于Distributed Representation的一种，它也是把词表示为语义空间中的一个向量。

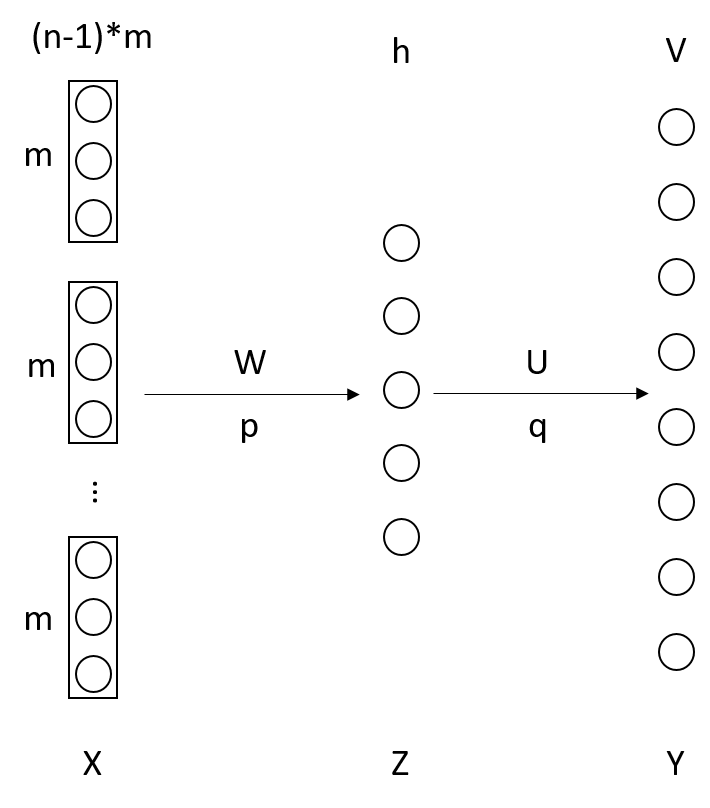
图1 基于神经网络的语言模型

每个词$w_i$用m维的向量表示，每个词受它前面的n-1个词的影响，把这n-1个词的向量首尾相连拼接起来构成输入层，所以输入层上有$(n-1)*m$个神经元。输出层上有V个神经元，V是所有词的总数，$y_i$表示输出为$w_i$的概率，对于训练集来说如果输入层上是$w_i$的前n-1个词的向量，则$y_i=1，y_k=0(k\ne{i})$。隐藏层上有h个神经元，h是个超参数，可以任意调。

通常n不会超过5，m在$10^1 \sim 10^2$量级，h在$10^2$量级。

\begin{equation}\left\{\begin{matrix}Z=tanh(W\cdot X+p) \\ Y=softmax(U\cdot Z+q)\end{matrix} \right . \end{equation}

输入层到隐藏层的权值矩阵为W，偏置为p。隐藏层的激活函数为tanh。隐藏层到输出层的权值矩阵为U，偏置为q。输出层是个softmax层，使得输出层形成一个概率分布。我在《神经网络调优》中讲过，输出层为softmax层时，目标函数常采用似然函数。这几乎就是个平常的3层全连接神经网络，说“几乎”是因为它跟平常的3层神经网络有一点不同：输入层（即每个词的词向量）也是需要通过学习得来的。

这个神经网络语言模型有2个好处：

1. 把词表示为连续的向量，而非离散的one-hot模式，这样就不需要像N-gram那样单独地处理零频问题了。
2. 词向量比较短，$10^1 \sim 10^2$量级，从而避免了稀疏性问题。

但也有1个不好的地方：就是从隐藏层到输出层计算量太大，需要$h*V$次乘法，$V$很大。word2vec算法就是用来解决这个计量大的问题的（作了这么多铺垫，主角终于要出场了）。

word2vec实际上有2种模型：CBoW和Skip-gram，这2种模型又都可以采用2种方法来优化：层次softmax法和负采样法。

CBoW(Continuous Bag of Words)

CBoW模型是根据$w_i$的上下文来预测$w_i$出现的概率。

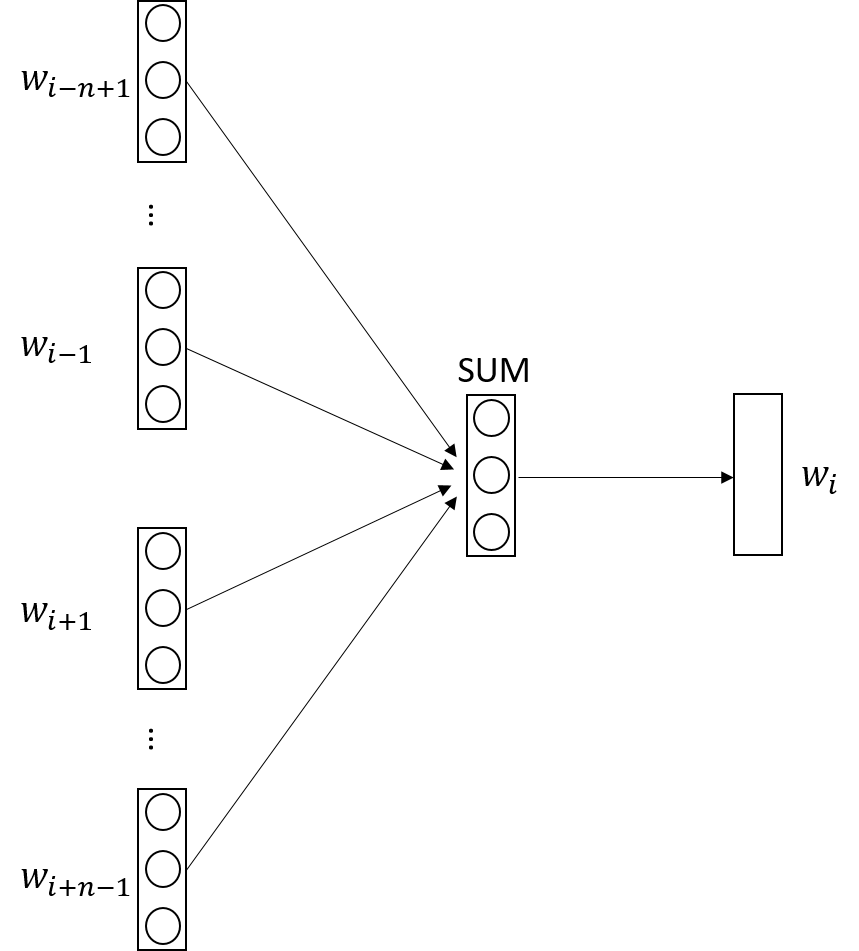
图2 CBow模型

输入层是$w_i$的context，即前后各取n-1个词，由2(n-1)个词向量拼接而成。

图2与图1的主要区别就在于隐藏层。图2中把输入层的2(n-1)个向量对应位置上相加，就形成了隐藏层。而在图1中输入层到隐藏层是一个普通的全连接，隐藏层神经元个数是任意定的。

从隐藏层到输出层也可以像图1那样做全连接，然后用softmax进行归一化，但这样计算量太大。具体的解决方案就是下文的Hierarchical Softmax和Negative Sampling。

Skip-gram

图3 Skip-gram模型

Skip-gram跟CBoW正好相反，它用$w_i$来预测$context_{w_i}$。$p(context_{w_i}|w_i)=p(w_{i-n+1}|w_i)p(w_{i-n+2}|w_i) \cdots p(w_{i+n-1}|w_i)$。$p(w_o|w_i)$是一个多项分布（多分类问题），可以用softmax来表示这个概率。

$$p(w_o|w_i)=\frac{e^{W_i \cdot W_o}}{\sum_j^V{e^{W_i \cdot W_j}}}$$

$W_j$是词$w_j$的向量化表示，$V$是词汇的总数。$p(w_o|w_i)$本质上是$W_i$和$W_o$的余弦相似度再做一次softmax归一化。这个归一化的求和运算量是很大的，解决办法得看下文的Hierarchical Softmax和Negative Sampling。

FastText算法对word2vec进行了改进，它在计算softmax不是让$W_i$和$W_o$两向量相乘，而是让$w_i$的n-gram与$W_o$相乘，即$\left(\sum_{i-n \le j \le i}{W_j}\right) \cdot W_o$。“我 爱 她” 这句话中的词袋模型特征是 “我”，“爱”, “她”。这些特征和句子 “她 爱 我” 的特征是一样的。如果加入 2-Ngram，第一句话的特征还有 “我-爱” 和 “爱-她”，这两句话 “我 爱 她” 和 “她 爱 我” 就能区别开来了。当然啦，为了提高效率，FastText过滤掉低频的 N-gram，另外对于非常高频的词只取1-gram，非高频词取3-gram到6-gram。因为高频语会导致更多的n-gram组合，这种组合越多计算量就越大。为了减少n-gram组合，而实践中可以对n-gram组合进行hashing，论文中把所有的n-gram组合映射到了200万个hash值。

Hierarchical Softmax

 原始的softmax计算$p(w_i|cond)$时要计算出所有的$p(w_j|cond), j \in \{1,2,\cdots,V\}$，然后再作归一化，计算复杂度为$O(V)$。而Hierarchical Softmax则采用了二分查找树，沿着树一层一层地计算出$p(w_i|cond)$，所以叫“层次”softmax。具体思路是这样的：我们把所有词汇分成互不相交的2个子集，$D_1$和$D_2$，则$p(D_1|cond)$可以用sigmoid函数来表示--因为这是个二分类问题。

$$p(D_1|cond)=\frac{1}{1+e^{-U_{D_1} \otimes B_1}}$$

$U_{D_1}$和$B_1$都是模型的参数，都是长度为m的向量，m是词向量的长度。$U_{D_1}$是集合$D_1$的向量化表示，$B_1$是与$U_{D_1}$对应的系数矩阵。需要注意的是$p(D_1|cond)$也是一个向量，上式中$U_{D_1} \otimes B_1$表示对应位置上的元素分别相乘，而不是求内积。

我们可以继续把$D_1$、$D_2$再各自分成2个子集，一直这样分下去，直到集合中只剩下一个词$w_i$，则$p(w_i|cond)=p(D_i|cond)p(D_j|D_i)p(D_k|D_j)\cdots$，只需要进行$log(V)$次sigmoid运算。

训练样本中各个$w$出现的次数不一样，所以在整个学习的过程中各个$p(w|cond)$计算的次数也不一样，对于出现越频繁的$w$我们希望它根节点越近，因为这样计算$p(w|cond)$的复杂度越小，很自然地我们就想到了Huffman树。

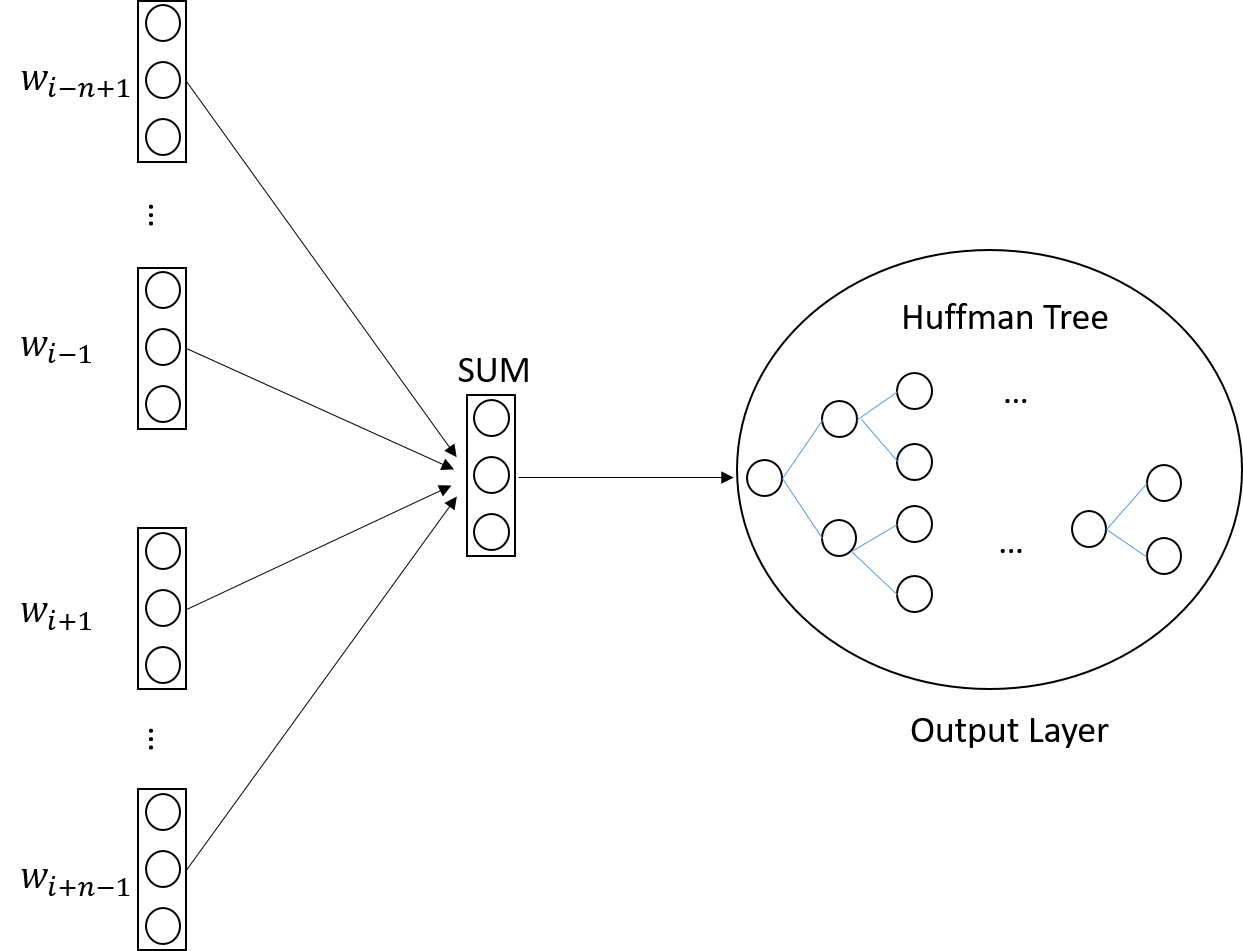
图4 基于Hierarchical Softmax的CBoW模型

同理，Skip-gram也可以结合Hierarchical Softmax使用，用Hierarchical Softmax代替原先的softmax输出层。

Negative Sampling

CBoW中的$p(w_i|context)$和Skip-gram中的$p(w_{i-n+1}|w_i)$都需要使用softmax在全局做归一化的，计算量很大，复杂度为$O(V)$。以Skip-gram为例，Negative Sampling认为

$$p(w_o|w_i)=\sigma(W_i \cdot W_o)\prod_{j=1}^k{(1-\sigma(W_i \cdot W_j))}$$

其中$\sigma(x)=\frac{1}{1+e^{-x}}$，简单推导得$\sigma(-x)=1-\sigma(x)$，这样得到的$p(w_o|w_i)$就已经是归一化之后的了，只需要进行k+1次sigmoid运算。

 即Negative Sampling认为$p(w_o|w_i)$等于$w_i$出现的时候$w_o$出现的概率乘上k个$w_j$都没有出现的概率。$w_j$是从语料库中随机抽取的词，用来当作背景噪声的代表，抽取了k个这样的噪声词。抽取噪声词时每个词被抽中的概率等于它在语料库是出现的概率。

“下采样”可以显著提高低频词的向量准确度，其基本思想是训练时随机丢掉那些高频的词。词被选中的概率为

$$p(w) = \sqrt{a}+\frac{1}{a},\;\;a=\frac{f(w)}{\beta*\sum_i{f(w_i)}}$$

$f(w)$是w在语料库是出现的频率，$\beta$是一个先验参数。当$a \ge 3$时，该词有一定的概率被丢弃（即进入了高频词的范筹）；当$a \le 2$时，该词一定会被选中。

实现

参数优化求解参见http://www.hankcs.com/nlp/word2vec.html或http://blog.csdn.net/fyuanfena/article/details/52791655

代码 https://github.com/Orisun/word2vec