支持向量机

结构风险最小化原则

经验风险：在训练样本上的误判，也就是损失函数了。

结构风险：由2部分组成，经验风险和VC置信范围VC Confidence。VC置信范围又跟训练样本数量和VC维有关，样本越多VC置信范围越小，VC维越大VC置信范围越大。VC维反映了函数集的学习能力，算法模型越复杂VC维越大。结构风险是模型在未知样本上的期望误判的上界，所以结构风险越小越好。结构风险最小化原则就是在兼顾经验风险最小的同时，还要尽量降低VC维（即降低模型复杂度，这跟奥卡姆剃刀原则是一致的）以减小VC置信范围。

当训练样本有限时如果只考虑经验风险，那么模型容易偏复杂，出现过拟合的现象。即训练样本有限时经验风险和真实风险差距较大。比如人工神经网络优化的就是经验风险，易陷入局部最优，训练结果不太稳定，一般需要大样本。而支持向量机优化的是结构风险，泛化能办强，算法具有全局最优性，是针对小样本统计的理论。

 SVM中的最优化问题

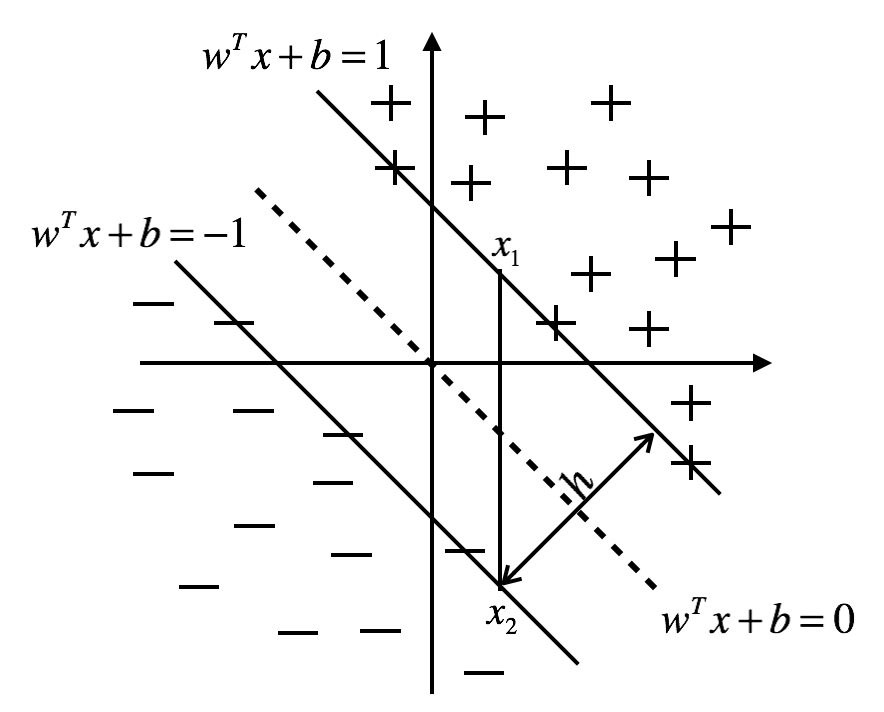
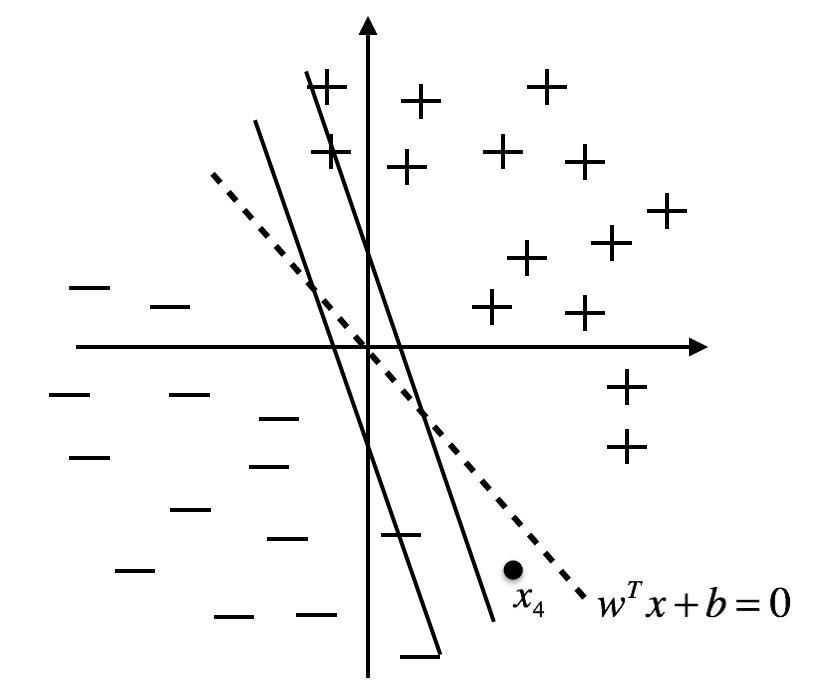
                 图1.结构风险最小化                                    图2.经验风险最小化

对于线性可分的二分类问题，正样本$x_i$在$w^{T}x+b=1$的上侧，即$w^{T}x_i+b\ge{1}$，负样本$x_j$在$w^{T}x+b=-1$的下侧，即$w^{T}x_j+b\le{-1}$，令正样本的分类标签$y_i=1$，负样本的分类标签$y_j=-1$，可以得到对正负样本都有$y_{i}(w^{T}x_i+b)\ge{1}$。

根据结构风险最小化的原则，SVM的优化目标是使两个分类平面之间的间隔（即h）最大，即得到图1所示的分类器，此时的分类决策函数是$w^{T}x+b=0$。图2所示的分类器在训练训练样本上的误差为0，即满足经验风险最小化。对于待预测的数据点$x_4$来说，图1所示的分类器会把它分负样本里面去，而图2所示的分类器会把它分到正样本里面去，所以SVM采用的是图1所示的分类器。

设$x_1$和$x_2$分别是$w^{T}x+b=1$和$w^{T}x+b=-1$上的点，两式相减得$w^{T}(x_1-x_2)=2$，这里w和x都是向量，下面我们要把向量的内积转换为代数乘积。w与分界面垂直，$x_1-x_2$在w方向上的投影长度为h，所以$w^{T}(x_1-x_2)=||w||*h=2$，所以$h=\frac{2}{||w||}$，SVM训练的目标是求$max\;h$时的w和b。

SVM转换为一个优化问题：

$\begin{matrix}\min&f(w,b)=\frac{1}{2}||w||^2\\s.t.&g(w,b)=y_{i}(w^{T}x_i+b)-1\ge{0}\end{matrix}$

构造拉格朗日函数$L(w,b,a)=\frac{1}{2}||w||^2+\sum_{i=1}^{N}a_i[1-y_i(w^{T}x+b)]$，其中$a_i\ge{0}$

根据我的另一篇博文KKT条件我们知道：

$\left.\begin{matrix}L(w,b,a)=\frac{1}{2}||w||^2+\sum_{i=1}^{N}a_i[1-y_i(w^{T}x+b)]\\a_i\ge{0}\\1-y_i(w^{T}x+b)\le{0}\end{matrix}\right\}$=>$\left\{\begin{matrix}\min_{w,b}f(w,b)=\min_{w,b}\max_{a}L(w,b,a)=\max_a\min_{w,b}L(w,b,a)=f(w^*,b^*)\\a_i[1-y_i(w^{*T}x+b^*)]=0\\\frac{\partial{L(w,b,a)}}{\partial{w^*}}=0\\\frac{\partial{L(w,b,a)}}{\partial{b^*}}=0\end{matrix}\right.$

\begin{equation}a_i[1-y_i(w^{*T}x+b^*)]=0\label{e}\end{equation}

\begin{equation}\frac{\partial{L(w,b,a)}}{\partial{w^*}}=0\label{pw}\end{equation}

\begin{equation}\frac{\partial{L(w,b,a)}}{\partial{b^*}}=0\label{pb}\end{equation}

由\eqref{pw}得\begin{equation}w-\sum_{i=1}^{N}a_{i}y_{i}x_{i}=0\label{w}\end{equation}

由\eqref{pb}得\begin{equation}\sum_{i=1}^{N}a_{i}y_i=0\label{b}\end{equation}

由\eqref{w}和\eqref{b}得$L(w,b,a)=\sum_{i=1}^{N}a_{i}-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}a_{i}a_{j}y_{i}y_{j}x_{i}^{T}x_j$

$\therefore$ \begin{equation}f(w^*,b^*)=\max_a\min_{w,b}L(w,b,a)=\max_a{\sum_{i=1}^{N}\sum_{j=1}^{N}a_{i}a_{j}y_{i}y_{j}\left \langle x_{i}^{T},x_j \right \rangle}\label{svm}\end{equation}

其中$\left \langle x_i^T,x\right \rangle$表示$x_i^T$和$x$的内积。

此时SVM的优化问题已转化为\eqref{svm}，待求参数是$a_i$，这个优化问题如何求解留到文章最后一部分讲解。

我们把落在分类平面上的点（即满足$y_{i}(w^{T}x_i+b)=0$）称为支持向量，由\eqref{e}得当$x_i$不是支持向量时$a_i=0$

由\eqref{w}得到分类决策函数\begin{equation}f(w,b)=w^{T}x+b=(\sum_{i=1}^{N}a_{i}y_{i}x_{i})^{T}+b=\sum_{i=1}^{N}a_{i}y_{i}\left \langle x_i^T,x\right \rangle+b\label{sign}\end{equation}

其中$x_i$是支持向量，因为对于非支持向量$a_i=0$，即$\sum_{i=1}^{N}a_{i}y_{i}\left \langle x_i^T,x\right \rangle=0$。

核技巧

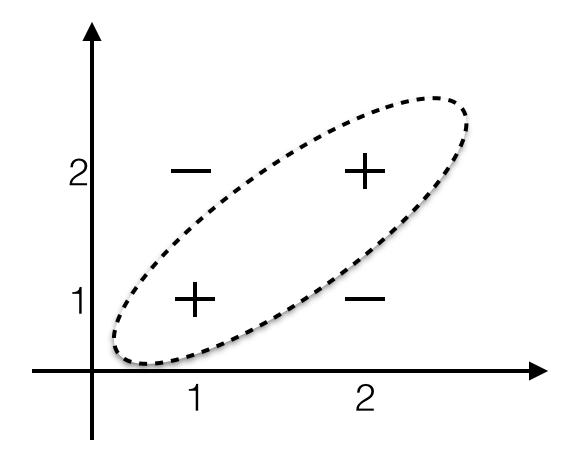
      图3.线性不可分

考虑图3线性不可分的情况，两个正样本分别是(1,1)和(2,2)，两个负样本分别是(1,2)和(2,1)。这种情况下分类平面是个如图3所示的曲面。

但是采用某种方法把2维空间中的点映射到5维空间后，就变得线性可分，关键看选用什么样的映射函数。比如我们采用下面的映射函数：

$(x_1,x_2)\rightarrow(x_1,x_1^2,x_2,x_2^2,x_{1}x_2)$

这样

$(1,1)\rightarrow(1,1,1,1,1)$

$(2,2)\rightarrow(4,4,4,4,4)$

$(1,2)\rightarrow(1,1,2,4,2)$

$(2,1)\rightarrow(2,4,1,1,2)$

令$A=(1,1,-1,-0.5-0.5)$，我们采用分类函数$f(X)=(A\cdot{X})^2$

这样

$f(1,1,1,1,1)=0$

$f(4,4,4,4,4)=0$

$f(1,1,2,4,2)=9$

$f(2,4,1,1,2)=12.25$

 我们取f(x)=4就可以将正负样本分开。

这里解释一下我们为什么把$f(X)=(A\cdot{X})^2$叫做线性分类器，这不明明是带了个平方吗？有个约定：如果g(x)是线性分类器，那么我们把f(g(x))称为广义线性分类器。比如Logitic分类器就是广义线性分类器，其分类函数是$g(x)=\frac{1}{1+e^{-\theta^{T}x}}$

回过头来看SVM的分类决策函数$\sum_{i=1}^{N}a_{i}y_{i}\left \langle x_i^T,x\right \rangle+b$，当样本点线性不可分时通过映射函数$\phi$将其映射到高维空间，$\sum_{i=1}^{N}a_{i}y_{i}\left \langle \phi(x_i^T),\phi(x)\right \rangle+b$。但是映射到高维后参数$a_i$也变成高维的，增加了计算量，这可怎么办呢？其实核函数K还有一个性质，就是$K(x_i^T,x)=\left \langle \phi(x_i^T),\phi(x)\right \rangle=\phi(\left \langle x_i^T,x\right \rangle)$，即两个数据映射到高维空间后再做内积等价于这两个数据先在低维空间做内积然后再把内积映射到高维空间。

这样SVM的分类决策函数\eqref{sign}就变成\begin{equation}\sum_{i=1}^{N}a_{i}y_{i}K(x_i^T,x)+b\label{sign_k}\end{equation}

要构造一个核函数并非易事，实践中常用的核函数有：

1. 多项式核函数$K(x_1,x_2)=(\left \langle x_1,x_2\right \rangle+R)^d$
2. 高斯核函数$K(x_1,x_2)=exp(-\frac{||x_1-x_2||^2}{2\sigma^2})$

 噪音问题

训练数据中会存在噪音，即正样本不满足$w^{T}x_i+b\ge{1}$，负样本不满足$w^{T}x_j+b\le{-1}$，此时的正负样本都满足：

$y_{i}(w^{T}x_i+b)\ge{1-\xi_i}$其中$\xi_i>0$称为松驰变量。

$\xi_i$不能太大，即我们对噪音的容忍是有限度的，所以目标函数为

$\begin{matrix}\min&\frac{1}{2}||w||^2+c\sum_{i=1}^N\xi_i\\s.t.&\xi_i>0\\ & c>0\\ & y_{i}(w^{T}x_i+b)\ge{1-\xi_i}\end{matrix}$

其中c用来控制权重。

略去拉格朗日函数的构造及对偶问题的证明，这里直接给出结论：带噪音的SVM转化为如下优化问题

$\begin{matrix}\max_a&\sum_{i=1}^{N}a_i-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}a_{i}a_{j}y_{i}y_{j}K(x_{i}^{T},x_j)\\s.t.&0\le{a_i}\le{c}\\&\sum_{i=1}^{N}a_{i}y_i=0\end{matrix}$

SMO算法

通过上文的推导，SVM转换为只需要求$a_i$的一个优化问题。优化方法有很多，SVM采用的是SMO（sequential minimal optimixation，序列最小优化）算法。

对于优化问题$\min_{a}f(a_1,a_2\ldots,a_N)$，SMO每次只优化一个变量$a_i$，固定其他变量$a_j(j\ne{i})$。基本流程如下

$k=0\\while(k<MaxIteration)\{\\\;\;\;\;for(i=1,i\le{N},i++)\{\\\;\;\;\;\;\;\;\;a_i=arg_{a}\max{f^{(k)}(a_1,a_2\ldots,a,a_j\ldots,a_N)}\\\;\;\;\;\}\\\;\;\;\;if(f^{(k)}\ge{f^{(k-1)})})\{\\\;\;\;\;\;\;\;\;break\\\;\;\;\;\}\\\;\;\;\;k++\\\}$

详细步骤就不讲了，如果要自己动手编码实现的话可以参考JerryLead的博客。