神经网络与深度学习笔记 Chapter 1.
转载请注明出处:http://www.cnblogs.com/zhangcaiwang/p/6875533.html
sigmoid neuron
微小的输入变化导致微小的输出变化,这种特性将会使得学习称为可能。但是在存在感知器的网络中,这是不可能的。有可能权重或偏置(bias)的微小改变将导致感知器输出的跳跃(从0到1),从而导致此感知器后面的网络以一种难以理解的方式发生巨大的改变。解决这一问题就要使用另外一种人工神经元-sigmoid神经元(也叫逻辑神经元)。
sigmoid神经元的输入不只是0或1,而且可以取[0,1]中的任何值,每一个输入有一个对应的权重。与此同时,输出也不再单纯为0或1,而是变为 σ(w⋅x+b)。其中:
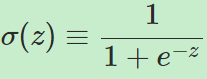 为sigmoid函数。
为sigmoid函数。
σ函数的数学形式是不重要的,重要的是它所表述的形状,它是阶梯函数的平滑版本。

根据微分,我们有
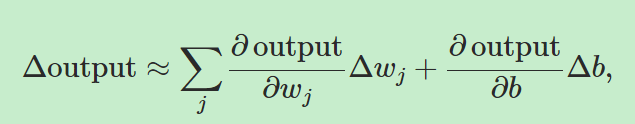
上面的式子表明了,输出的增量与bias和权重的增量是呈近似线性关系的,也就是说满足了“微小的输入变化导致微小的输出变化”这个条件,这是一个好消息。那么为什么要用sigmoid函数表示σ而不是其他的数学形式?其实也是可以的,但是sigmoid函数的这种形式在求偏导数的时候比较简单,而且被用的很多。
The architecture of neural networks
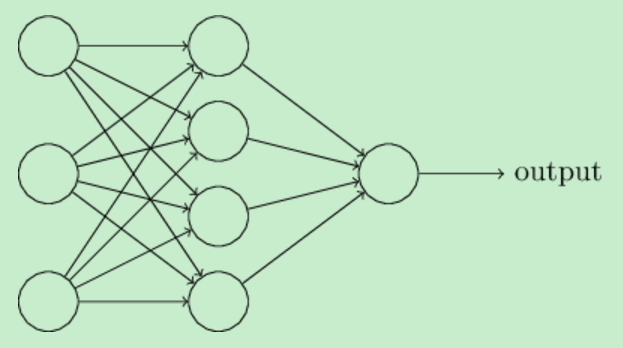
本部分阐述神经网络中所用到的术语。
在最左边的输入层中的神经元叫做输入神经元(input neuron),对应地,最右边中的输出层中的神经元被称为输出神经元(output neuron)1
输入层和输出层中间的一些层叫做隐藏层(hidden layer),只是用来表征它们既不是输入层也不是输出层。
上图中的多层神经网络一般被称为多层感知器(multilayer perceptrons)或者MLPs,不过它与感知器没有半毛钱关系,因为它的最小单位是sigmoid神经元。
在我们的笔记中所描述的神经网络中一个神经元的输出作为另一个神经元的输入,这种形式称为feedforward(前向反馈或者正反馈),不允许存在负反馈的情况,如果存在的话则会产生线程中所说的死锁。但是确实存在有负反馈或者称为循环的神经网络,就叫做循环神经网络(RNN, recurrent neural network).
识别手写数字的简单网络
这个问题可以分为两个子问题。其一,把图片中连续的数字分开。如图所示
![]() --------------------------->
--------------------------->![]()
第二个问题就是把分开的子图中的内容识别。本笔记解决第二个问题。
这里我们用一个三层神经网络解决第二个问题:
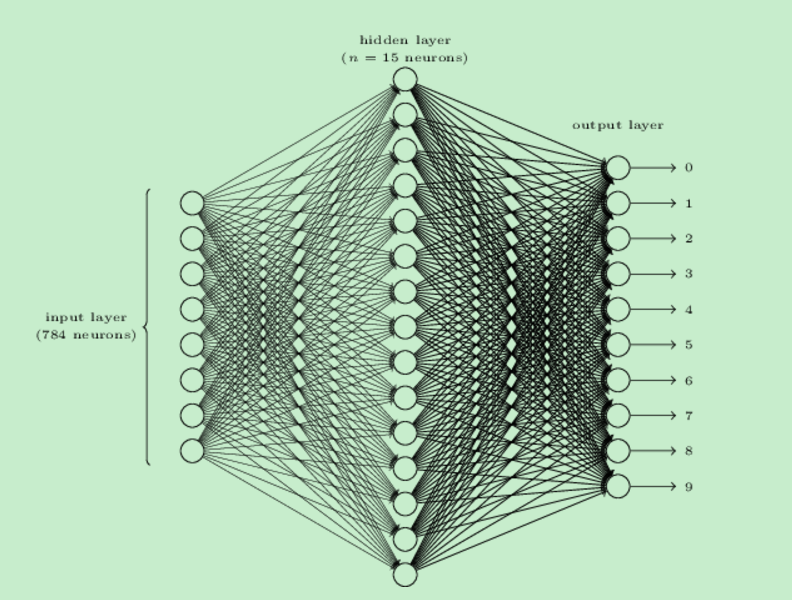
我们后续要处理的图片的规格为28*28,也就是每张图片有784个像素,我们为每一个输入设定一个输入神经元。输入神经元表示灰度,0.0是白,1.0是黑。
Learning with gradient descent
我们构建代价函数(cost function),又叫做目标函数(objective function)或者损失函数(loss function):
上式中,w代表权重,b代表bias,n代表训练样本数,a代表由10维的神经网络输出向量。C被叫做二次代价函数(quadratic cost function),也被叫做均方误差(mean squared error)或MSE。我们的目标是让C越小越好,为了解决这个问题,我们需要用到梯度下降(gradient descent)。那么为什么我们要用二次代价函数而不是直接用正确识别的数目来学习?因为二次代价函数是平滑的函数,对于微小的输入输出也会有微小的改变。但是正确识别的图片数目却不是平滑的,改变权重或bias之后有可能失败数目不变,那么接下来就不知道如何调整权重或bias。所以我们用二次代价函数来学习。
为了解决最小化C的问题,我们用v代替w和b。并用梯度下降方法解决。假定C是关于v1和v2两个变量的函数:
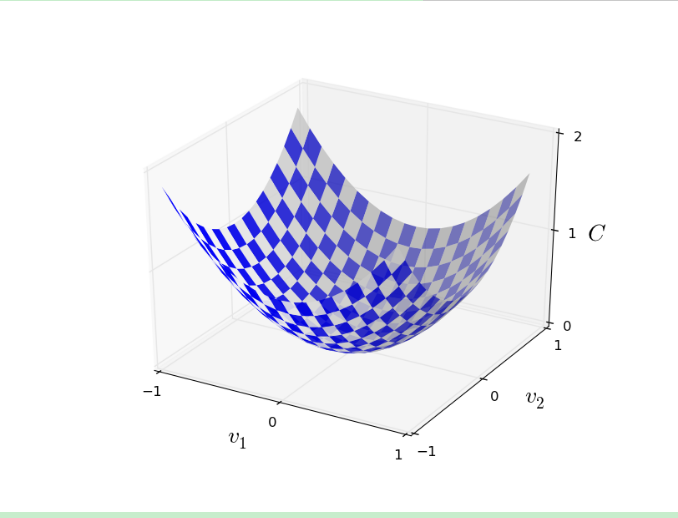
我们有

我们用∇C来表示梯度向量,则有
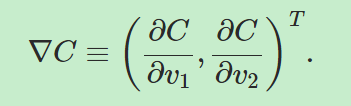
那么我们可以把ΔC近似写为: ![]()
那么我们应该如何选择Δv呢?一般来说我们会令![]() ,其中的η被称作学习率(learning rate),是一个很小的、正数。那么从而有:
,其中的η被称作学习率(learning rate),是一个很小的、正数。那么从而有:

所以,在这个设定下,ΔC一直会小于0,也就是说C一直在变小。从而有v的更新公式:
![]()
那么,如何把梯度下降用到我们的神经网络中呢?这里我们用wk和bl代替v,从而有更新公式:
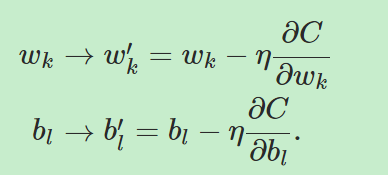
在梯度下降方法的应用中存在一些问题,对于这些问题的深入探讨将在以后的章节中进行,这里考虑其中一个问题。对于![]() 我们有
我们有![]() ,其中
,其中![]() 。在实际中,为了计算∇C我们需要计算每一个输入x的梯度,当输入很多的时候这将会非常耗费时间。一个叫做随机梯度下降(stochastic gradient descent)的方法可以加快学习的速度。
。在实际中,为了计算∇C我们需要计算每一个输入x的梯度,当输入很多的时候这将会非常耗费时间。一个叫做随机梯度下降(stochastic gradient descent)的方法可以加快学习的速度。
随机梯度下降的主要思想是,在输入中随机选择一部分值计算梯度,并把他们作为所有输入梯度的近似值,用这些梯度的平均值更新权重和bias;接下来从剩余的样本中选择输入用于重复这一过程,直到所有的样本被用完,这个过程的完成被称为完成了一个训练代( an epoch of training)。比如从n个输入中随机选择m个样本,则有:
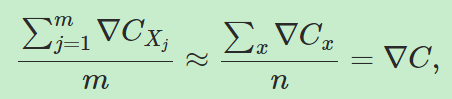 ,也就是有,
,也就是有,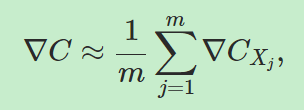 。
。
那么权重和bias的训练过程为:

有时候我们会把n,m省略,因为我们不可能一直知道m和n的数值,尤其是在实时环境中。实际上我们是一直在改变学习率η,这与我们之前说的有点不同。随机梯度下降的原理是我们并不需要精确计算梯度,我们只需要知道代价函数C下降的一个大致方向就行了。
Implementing our network to classify digits
首先给出一个表示神经网络的类:
class Network(object): def __init__(self, sizes): self.num_layers = len(sizes) self.sizes = sizes self.biases = [numpy.random.randn(y, 1) for y in sizes[1:]] self.weights = [numpy.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])]
其中size类似于[3,2,1]的形式,每一维代表一层网络的神经元数。nump.random.randn()用于获取一个符合正态分布的随机数,参数为任意正整数表示维度。对于zip函数有:
>>> zip([1,2],[3,4])
[(1, 3), (2, 4)]
self.weights[1]是一个(y,x)矩阵,其中y是第三层的神经元个数,x是第二层神经元个数。
对于
![]()
其中的a是第二层的激活值矩阵,a'是第三层的激活值矩阵,w是权重矩阵,b是第二层到第三层的bias。
我们定义sigmoid函数:
def sigmoid(z): return 1.0/(1.0+numpy.exp(-z))
对于sigmoid函数,如果输入的是向量,那么就会返回一个包含结果的向量。注意这里的向量是![]() 的形式。
的形式。
定义计算激活值的函数如下:
def feedforward(self, a): """Return the output of the network if "a" is input.""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a
下面给出的是实现批量随机梯度下降的SGD函数
training_data:是输入和输出元组(x,y)构成的列表,x代表输入图片,y代表输出的预测值
epochs:训练多少代
mimi_batch_size:采样的输入数目
eta: η,学习率
test_data: 检验数据
def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None): """Train the neural network using mini-batch stochastic gradient descent. The "training_data" is a list of tuples "(x, y)" representing the training inputs and the desired outputs. The other non-optional parameters are self-explanatory. If "test_data" is provided then the network will be evaluated against the test data after each epoch, and partial progress printed out. This is useful for tracking progress, but slows things down substantially.""" if test_data: n_test = len(test_data) n = len(training_data) for j in xrange(epochs): random.shuffle(training_data) #打乱输入 mini_batches = [ #将输入按mini_batch分组,不能均分的话,最后一个分组包含剩余不足mini_batch个数的输入 training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: #对每一个批量输入进行梯度下降计算,更新权重和bias,update_mini_batch为梯度下降算法。 self.update_mini_batch(mini_batch, eta) if test_data: print "Epoch {0}: {1} / {2}".format( j, self.evaluate(test_data), n_test) else: print "Epoch {0} complete".format(j)
def update_mini_batch(self, mini_batch, eta): """Update the network's weights and biases by applying gradient descent using backpropagation to a single mini batch. The "mini_batch" is a list of tuples "(x, y)", and "eta" is the learning rate.""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) #求损失函数对每一个权重和bias的微分 nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)]
delta_nabla_b, delta_nabla_w = self.backprop(x, y)这一行表示的用反向传播算法(backpropagation algorithm)计算随机梯度下降。这一部分讲在chapter2中展开。
下面给出程序的运行过程,其中mnist_loader.py用于吧数据集分成三部分。
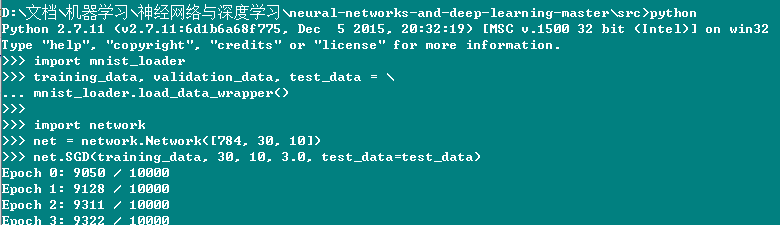
..............
...............
................

源代码以及数据集见https://github.com/mnielsen/neural-networks-and-deep-learning/archive/master.zip
由于bias和权重的初始化值不一样,所以每次跑出来的结果也是不一样的。而且,对于训练代数、中间隐含层个数、学习率的选取也会影响结果。
参考资料:http://neuralnetworksanddeeplearning.com/chap1.html#eqtn3

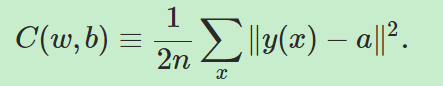



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步