ACM-ICPC 2018 南京赛区网络预赛（蒟蒻刷题）

.A. An Olympian Math Problem

 

Alice, a student of grade 666, is thinking about an Olympian Math problem, but she feels so despair that she cries. And her classmate, Bob, has no idea about the problem. Thus he wants you to help him. The problem is:

We denote k!k!k!:

k!=1×2×⋯×(k−1)×kk! = 1 \times 2 \times \cdots \times (k - 1) \times kk!=1×2×⋯×(k−1)×k

We denote SSS:

S=1×1!+2×2!+⋯+S = 1 \times 1! + 2 \times 2! + \cdots +S=1×1!+2×2!+⋯+
(n−1)×(n−1)! (n - 1) \times (n-1)!(n−1)×(n−1)!

Then SSS module nnn is ____________

You are given an integer nnn.

You have to calculate SSS modulo nnn.

Input

The first line contains an integer T(T≤1000)T(T \le 1000)T(T≤1000), denoting the number of test cases.

For each test case, there is a line which has an integer nnn.

It is guaranteed that 2≤n≤10182 \le n\le 10^{18}2≤n≤1018.

Output

For each test case, print an integer SSS modulo nnn.

Hint

The first test is: S=1×1!=1S = 1\times 1!= 1S=1×1!=1, and 111 modulo 222 is 111.

The second test is: S=1×1!+2×2!=5S = 1\times 1!+2 \times 2!= 5S=1×1!+2×2!=5 , and 555 modulo 333 is 222.

 

样例输入

 

2
2
3

 

样例输出

 

1
2

solution
打表发现为x-1
推了一会不知道为啥
CODE:

#include<bits/stdc++.h>
using namespace std;
#define int long long

int cal(int x,int p)
{
    int ans = 1;
    for(int i=1;i<=x;i++)
    ans*=i,ans%=p;
    return ans;
}
void work(int x)
{
    int ans = 0;
    for(int i=1;i<x;i++)
    ans =(ans+i*cal(i,x))%x;
    cout<<x<<" "<<ans<<endl;
}
signed main()
{
  int T;
  for(cin>>T;T;T--)
  {
    int x;cin>>x;
    cout<<x-1<<endl;
  }
  return 0;
    for(int i=1;i<=100;i++)
    work(i);
}

 

---

---

---

B. The writing on the wall

Feeling hungry, a cute hamster decides to order some take-away food (like fried chicken for only 303030 Yuan).

However, his owner CXY thinks that take-away food is unhealthy and expensive. So she demands her hamster to fulfill a mission before ordering the take-away food. Then she brings the hamster to a wall.

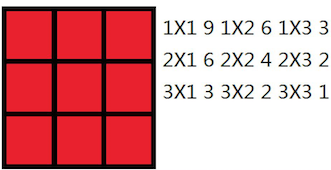
The wall is covered by square ceramic tiles, which can be regarded as a n∗mn * mn∗m grid. CXY wants her hamster to calculate the number of rectangles composed of these tiles.

For example, the following 3∗33 * 33∗3 wall contains 363636 rectangles:

Such problem is quite easy for little hamster to solve, and he quickly manages to get the answer.

Seeing this, the evil girl CXY picks up a brush and paint some tiles into black, claiming that only those rectangles which don't contain any black tiles are valid and the poor hamster should only calculate the number of the valid rectangles. Now the hamster feels the problem is too difficult for him to solve, so he decides to turn to your help. Please help this little hamster solve the problem so that he can enjoy his favorite fried chicken.

Input

There are multiple test cases in the input data.

The first line contains a integer TTT : number of test cases. T≤5T \le 5T≤5.

For each test case, the first line contains 333 integers n,m,kn , m , kn,m,k , denoting that the wall is a n×mn \times mn×m grid, and the number of the black tiles is kkk.

For the next kkk lines, each line contains 222 integers: x yx\ yx y ,denoting a black tile is on the xxx-th row and yyy-th column. It's guaranteed that all the positions of the black tiles are distinct.

For all the test cases,

1≤n≤105,1≤m≤1001 \le n \le 10^5,1\le m \le 1001≤n≤105,1≤m≤100,

0≤k≤105,1≤x≤n,1≤y≤m0 \le k \le 10^5 , 1 \le x \le n, 1 \le y \le m0≤k≤105,1≤x≤n,1≤y≤m.

It's guaranteed that at most 222 test cases satisfy that n≥20000n \ge 20000n≥20000.

Output

For each test case, print "Case #xxx: ansansans" (without quotes) in a single line, where xxx is the test case number and ansansans is the answer for this test case.

Hint

The second test case looks as follows:

样例输入

2
3 3 0
3 3 1
2 2

样例输出

Case #1: 36
Case #2: 20

solution：
暴力的也可以过，枚举每个点作为矩形的左下角
code：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int b[100010][110], up[110];
int main(){
    int T, cas=0;
    scanf("%d", &T);
    while(T--){
        int n, m, K;
        scanf("%d%d%d", &n, &m, &K);
        for(int i=0; i<=n; i++){
            for(int j=0; j<=m; j++){
                b[i][j]=0;
                up[j]=0;
            }
        }
        for(int i=0; i<K; i++){
            int x, y;
            scanf("%d%d", &x, &y);
            b[x][y]=1;
        }
        ll ans=0;
        for(int i=1; i<=n; i++){
            for(int j=1; j<=m; j++){
                if(b[i][j]){
                    up[j]=i;
                }
            }
            for(int j=1; j<=m; j++){
                ll minn=0x7f7f7f7f7f7f7f7f;
                for(int k=j; k>0; k--){
                    minn=min(minn, (ll)(i-up[k]));
                    ans+=minn;
                }
            }
        }
        printf("Case #%d: %lld\n", ++cas, ans);
    }
    return 0;
}

 

---

---

 L. Magical Girl Haze

There are NN cities in the country, and MMdirectional roads from uu to v(1\le u, v\le n)v(1≤u,v≤n). Every road has a distance c_ici​. Haze is a Magical Girl that lives in City 11, she can choose no more than KK roads and make their distances become 00. Now she wants to go to City NN, please help her calculate the minimum distance.

Input

The first line has one integer T(1 \le T\le 5)T(1≤T≤5), then following TT cases.

For each test case, the first line has three integers N, MN,M and KK.

Then the following MM lines each line has three integers, describe a road, U_i, V_i, C_iUi​,Vi​,Ci​. There might be multiple edges between uu and vv.

It is guaranteed that N \le 100000, M \le 200000, K \le 10N≤100000,M≤200000,K≤10,
0 \le C_i \le 1e90≤Ci​≤1e9. There is at least one path between City 11 and City NN.

Output

For each test case, print the minimum distance.

样例输入复制

1
5 6 1
1 2 2
1 3 4
2 4 3
3 4 1
3 5 6
4 5 2

样例输出复制

3

solution
以后认真读题，像我以为是双向边卡了一晚上

dp的思想  dp i j  表示到达i点减少了j次路径的最短距离
然后我spfa被卡了。。。。
以后最短是还是迪杰斯特拉比较稳

CODE:

#include<bits/stdc++.h>

using namespace std;
#define ll long long
#define int long long
#define sccc(a,b,c) scanf("%lld %lld %lld",&(a),&(b),&(c));

int n,m,k;
const int N = 100010;

struct aa
{
    int so;
    ll w;
};

vector<aa>G[N];
ll dp[N][20];
int vis[N][15];

struct bb
{
    int x,y;
    ll w;
    bool operator<(const bb b)const
    {
        return w>b.w;
    }
};

void work()
{
    for(int i=1; i<=n; i++)
        for(int j=0; j<=k; j++)dp[i][j]=1e18,vis[i][j]=0;

    dp[1][0]=0;

    priority_queue<bb >q;

    q.push({1,0,0});

    while(!q.empty())
    {
        bb t=q.top();
        q.pop();
        if(vis[t.x][t.y])continue;
        vis[t.x][t.y]=1;
        for(auto i:G[t.x])
        {
            int so=i.so;
           ll w=i.w;
            if(dp[so][t.y]>dp[t.x][t.y]+w)
            {
                dp[so][t.y]=dp[t.x][t.y]+w;
                if(!vis[so][t.y])
                {
                    q.push({so,t.y,dp[so][t.y]});
                }
            }
            
            if(t.y<k)
            {
                if(dp[so][t.y+1]>dp[t.x][t.y])
                {
                    dp[so][t.y+1]=dp[t.x][t.y];
                    if(!vis[so][t.y+1])
                    {
                       q.push({so,t.y+1,dp[so][t.y+1]});
                    }
                }
            }


        }
        

    }

    ll ans = 1e18;
    for(int i=0;i<=k;i++)
    {
        ans = min(ans,dp[n][i]);
    }
    cout<<ans<<endl;

}
signed main()
{

 int T;
    for(cin>>T; T; T--)
    {
        scanf("%lld %lld %lld",&(n),&(m),&(k));
        for(int i=1; i<=n; i++)G[i].clear();
        for(int i=1; i<=m; i++)
        {
            int l,r,z;
           scanf("%lld %lld %lld",&(l),&(r),&(z));
            G[l].push_back({r,z});
        }
        work();

    }
}

 

 

---

---

---

J. Sum

A square-free integer is an integer which is indivisible by any square number except 111. For example, 6=2⋅36 = 2 \cdot 36=2⋅3 is square-free, but 12=22⋅312 = 2^2 \cdot 312=22⋅3 is not, because 222^222 is a square number. Some integers could be decomposed into product of two square-free integers, there may be more than one decomposition ways. For example, 6=1⋅6=6⋅1=2⋅3=3⋅2,n=ab6 = 1\cdot 6=6 \cdot 1=2\cdot 3=3\cdot 2, n=ab6=1⋅6=6⋅1=2⋅3=3⋅2,n=ab and n=ban=ban=ba are considered different if a=ba \not = ba​=b. f(n)f(n)f(n) is the number of decomposition ways that n=abn=abn=ab such that aaa and bbb are square-free integers. The problem is calculating ∑i=1nf(i)\sum_{i = 1}^nf(i)∑i=1n​f(i).

Input

The first line contains an integer T(T≤20)T(T\le 20)T(T≤20), denoting the number of test cases.

For each test case, there first line has a integer n(n≤2⋅107)n(n \le 2\cdot 10^7)n(n≤2⋅107).

Output

For each test case, print the answer ∑i=1nf(i)\sum_{i = 1}^n f(i)∑i=1n​f(i).

Hint

∑i=18f(i)=f(1)+⋯+f(8)\sum_{i = 1}^8 f(i)=f(1)+ \cdots +f(8)∑i=18​f(i)=f(1)+⋯+f(8)
=1+2+2+1+2+4+2+0=14=1+2+2+1+2+4+2+0=14=1+2+2+1+2+4+2+0=14.

样例输入

2
5
8

样例输出

8
14

solution

对线性筛的过程不熟悉，这题也不会做qwq
一个数如果有贡献的话，那他质因数分解之后不能有质因子的指数大于等于3
从线筛的时候搞一下就行了

CODE:

#include "bits/stdc++.h"
using namespace std;


const int N = 2e7+10;
int vis[N];
int pre[N];
int pcnt;
int ans[N];

void Pre()
{
    int mx=2e7;
    ans[1]=1;
    for(int i=2; i<=mx; i++)
    {
        if(!vis[i])pre[++pcnt]=i,ans[i]=2;
        for(int j=1; j<=pcnt&&1ll*pre[j]*i<=1ll*mx; j++)
        {
            vis[i*pre[j]]=1;
            if(i%pre[j] == 0)
            {
                int tp=pre[j]*pre[j];
                if(i%tp==0)ans[i*pre[j]]=0;/// 有大于等于三个
                else ans[i*pre[j]]=ans[i/pre[j]];/// 有两个
                break;
            }
            else ans[i*pre[j]]=ans[i]*ans[pre[j]];/// 只有一个
        }
    }

}

signed main()
{
    Pre();
    int T;
    cin>>T;
    while(T--)
    {
        int n;
        cin>>n;
        int tot=0;
        for(int i=1; i<=n; i++)
        {
            tot += ans[i];
        }

        cout<<tot<<endl;;
    }

}

 

---

---

---

E. AC Challenge

Dlsj is competing in a contest with n(0<n≤20)n (0 < n \le 20)n(0<n≤20) problems. And he knows the answer of all of these problems.

However, he can submit iii-th problem if and only if he has submitted (and passed, of course) sis_isi​ problems, the pi,1p_{i, 1}pi,1​-th, pi,2p_{i, 2}pi,2​-th, ........., pi,sip_{i, s_i}pi,si​​-th problem before.(0<pi,j≤n,0<j≤si,0<i≤n)(0 < p_{i, j} \le n,0 < j \le s_i,0 < i \le n)(0<pi,j​≤n,0<j≤si​,0<i≤n) After the submit of a problem, he has to wait for one minute, or cooling down time to submit another problem. As soon as the cooling down phase ended, he will submit his solution (and get "Accepted" of course) for the next problem he selected to solve or he will say that the contest is too easy and leave the arena.

"I wonder if I can leave the contest arena when the problems are too easy for me."
"No problem."
—— CCF NOI Problem set

If he submits and passes the iii-th problem on ttt-th minute(or the ttt-th problem he solve is problem iii), he can get t×ai+bit \times a_i + b_it×ai​+bi​ points. (∣ai∣,∣bi∣≤109)(|a_i|, |b_i| \le 10^9)(∣ai​∣,∣bi​∣≤109).

Your task is to calculate the maximum number of points he can get in the contest.

Input

The first line of input contains an integer, nnn, which is the number of problems.

Then follows nnn lines, the iii-th line contains si+3s_i + 3si​+3 integers, ai,bi,si,p1,p2,...,psia_i,b_i,s_i,p_1,p_2,...,p_{s_i}ai​,bi​,si​,p1​,p2​,...,psi​​as described in the description above.

Output

Output one line with one integer, the maximum number of points he can get in the contest.

Hint

In the first sample.

On the first minute, Dlsj submitted the first problem, and get 1×5+6=111 \times 5 + 6 = 111×5+6=11 points.

On the second minute, Dlsj submitted the second problem, and get 2×4+5=132 \times 4 + 5 = 132×4+5=13 points.

On the third minute, Dlsj submitted the third problem, and get 3×3+4=133 \times 3 + 4 = 133×3+4=13 points.

On the forth minute, Dlsj submitted the forth problem, and get 4×2+3=114 \times 2 + 3 = 114×2+3=11 points.

On the fifth minute, Dlsj submitted the fifth problem, and get 5×1+2=75 \times 1 + 2 = 75×1+2=7 points.

So he can get 11+13+13+11+7=5511+13+13+11+7=5511+13+13+11+7=55 points in total.

In the second sample, you should note that he doesn't have to solve all the problems.

样例输入1

5
5 6 0
4 5 1 1
3 4 1 2
2 3 1 3
1 2 1 4

样例输出1

55

样例输入2

1
-100 0 0

样例输出2

0

solution

状压水题
然后这题用当前状态更新后面的状态比较好处理
而不是那当前的状态去找前面的状态
然后就是最后不一定做完。。。

CODE:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
struct Node{
    long long a,b;
    vector<int> pre;
    bool flag(int k){//用来判断前置条件是否满足，即是否可以做这题
        for(int i = 0;i < pre.size();i++){
            if(((1<<(pre[i]-1))&k) == 0)    return false;
        }
        return true;
    }

}ac[25];
long long dp[1<<21];//一共最多2^20种状态
int main()
{
    int n;
    scanf("%d",&n);
    long long  a,b;
    int s,pre;
    for(int i = 1;i <= n;i++){
        scanf("%lld%lld%d",&a,&b,&s);
        ac[i].a = a;
        ac[i].b = b;
        for(int j = 0;j < s;j++){
            scanf("%d",&pre);
            (ac[i].pre).push_back(pre);
        }
    }
    //for(int i = 1;i <= n;i++)    cout << (ac[i].pre).size()<<endl;
    dp[0] = 0;
    for(int i = 1;i <= (1<<n);i++)    dp[i] = -100000000000;
    long long ans = 0;
    for(int i = 0; i < (1<<n);i++){
        long long t = 1;
        for(int j = 0;j < n;j++)
            if((1<<j)&i)    t++;//已经做出来几题，也就是已经用了几分钟
        for(int j = 1;j <= n;j++)
            if(ac[j].flag(i) && (((1<<(j-1))&i) == 0))//当第j题可以做，并且j题没有被做过时
            dp[i|(1<<(j-1))] = max(dp[i|(1<<(j-1))],dp[i] + t*ac[j].a + ac[j].b);
    }
    for(int i = 0;i < (1<<n);i++)
        ans = max(ans,dp[i]);
    printf("%lld\n",ans);
    return 0;
}

 

---

---

 

I. Skr

A number is skr, if and only if it's unchanged after being reversed. For example, "12321", "11" and "1" are skr numbers, but "123", "221" are not. FYW has a string of numbers, each substring can present a number, he wants to know the sum of distinct skr number in the string. FYW are not good at math, so he asks you for help.

Input

The only line contains the string of numbers SSS.

It is guaranteed that 1≤S[i]≤91 \le S[i] \le 91≤S[i]≤9, the length of SSS is less than 200000020000002000000.

Output

Print the answer modulo 100000000710000000071000000007.

样例输入1

111111

样例输出1

123456

样例输入2

1121

样例输出2

135

Solution

状压水题
差不多是个回文树的板子吧
建完树之后从0和1节点向下dfs就行了
dfs的时候算一下当前节点的值

CODE:

#include <queue>
#include <cstdio>
#include <set>
#include <string>
#include <stack>
#include <cmath>
#include <climits>
#include <map>
#include <cstdlib>
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#define  ULL unsigned long long
typedef long long ll;
using namespace std;
const int MAXN = 2e6+10 ;
const ll MOD =1e9+7;
const int N = 11 ;
char s[MAXN];
int hund[MAXN];
struct Palindromic_Tree
{
    int next[MAXN][N] ;//next指针，next指针和字典树类似，指向的串为当前串两端加上同一个字符构成
    int fail[MAXN] ;//fail指针，失配后跳转到fail指针指向的节点
    int cnt[MAXN] ;
    //int num[MAXN] ; // 当前节点通过fail指针到达0节点或1节点的步数(fail指针的深度)
    int len[MAXN] ;//len[i]表示节点i表示的回文串的长度
    int S[MAXN] ;//存放添加的字符
    int last ;//指向上一个字符所在的节点，方便下一次add
    int n ;//字符数组指针
    int p ;//节点指针
    int newnode(int l)     //新建节点
    {
        for(int i = 0 ; i < N ; ++ i) next[p][i] = 0 ;
        //cnt[p] = 0 ;
        //num[p] = 0 ;
        len[p] = l ;
        return p ++ ;
    }
    void init()   //初始化
    {
        p = 0 ;
        newnode(0) ;
        newnode(-1) ;
        last = 0 ;
        n = 0 ;
        S[n] = -1 ;//开头放一个字符集中没有的字符，减少特判
        fail[0] = 1 ;
    }
    int get_fail(int x)     //失配后，在回文串x中的所有后缀里找到一个串右端+s[n]依然构成回文串
    {
        //这里因为一定是从长的找到最短的，所以找到的一定是最长的
        while(S[n - len[x] - 1] != S[n]) x = fail[x] ;//判断此时S[n-len[last]-1]是否等于S[n]
        //即上一个串-1的位置和新添加的位置是否相同，相同则说明构成回文，否则，last=fail[last]。
        return x ;
    }
    void add(int c)   //cur,last,now都代表一个字符串，而不是一个下标/字符
    {
        c -= '0';
        S[++ n] = c ;   //n代表字符下标
        int cur = get_fail(last) ;   //通过上一个回文串找这个回文串的匹配位置
        //printf("%d ",cur);     //c+cur+c代表以c结尾的最长的回文串,cur对应原串中的位置就是以c前一个字符结尾的子串的位置
        if(!next[cur][c])     //如果这个回文串没有出现过，说明出现了一个新的本质不同的回文串
        {
            int now = newnode(len[cur] + 2) ;   //新建节点
            fail[now] = next[get_fail(fail[cur])][c] ;   //和AC自动机一样建立fail指针，以便失配后跳转
            next[cur][c] = now ;
            //num[now] = num[fail[now]] + 1 ;
        }
        last = next[cur][c] ;
        //cnt[last] ++ ;
    }
    void count()
    {
        for(int i = p - 1 ; i >= 0 ; -- i) cnt[fail[i]] += cnt[i] ;
        //父亲累加儿子的cnt，因为如果fail[v]=u，则u一定是v的子回文串！
    }
} run;

int ans;
void dfs(int u,int val)
{
    int v,inc;
    int tmp;
    for(int i=0; i<10; i++)
    {
        if(run.next[u][i])
        {
            v=run.next[u][i];
            tmp=run.len[v]-1?hund[run.len[v]-1]:0;
            inc=(val+i+1ll*i*tmp%MOD)%MOD;
            ans=(ans+inc)%MOD;
            dfs(v,1ll*inc*10%MOD);
        }
    }
}



int main()
{
    scanf("%s",&s);
    int n=strlen(s);
    run.init();
    for(int i=0; i<n; i++) run.add(s[i]);
    hund[0]=1;
    for(int i=1; i<=n; i++) hund[i]=1ll*hund[i-1]*10%MOD;
    dfs(0,0);
    dfs(1,0);
    printf("%d\n",ans);
    return 0;

}

 

---

---

G. Lpl and Energy-saving Lamps

During tea-drinking, princess, amongst other things, asked why has such a good-natured and cute Dragon imprisoned Lpl in the Castle? Dragon smiled enigmatically and answered that it is a big secret. After a pause, Dragon added:

— We have a contract. A rental agreement. He always works all day long. He likes silence. Besides that, there are many more advantages of living here in the Castle. Say, it is easy to justify a missed call: a phone ring can't reach the other side of the Castle from where the phone has been left. So, the imprisonment is just a tale. Actually, he thinks about everything. He is smart. For instance, he started replacing incandescent lamps with energy-saving lamps in the whole Castle...

Lpl chose a model of energy-saving lamps and started the replacement as described below. He numbered all rooms in the Castle and counted how many lamps in each room he needs to replace.

At the beginning of each month, Lpl buys mmm energy-saving lamps and replaces lamps in rooms according to his list. He starts from the first room in his list. If the lamps in this room are not replaced yet and Lpl has enough energy-saving lamps to replace all lamps, then he replaces all ones and takes the room out from the list. Otherwise, he'll just skip it and check the next room in his list. This process repeats until he has no energy-saving lamps or he has checked all rooms in his list. If he still has some energy-saving lamps after he has checked all rooms in his list, he'll save the rest of energy-saving lamps for the next month.

As soon as all the work is done, he ceases buying new lamps. They are very high quality and have a very long-life cycle.

Your task is for a given number of month and descriptions of rooms to compute in how many rooms the old lamps will be replaced with energy-saving ones and how many energy-saving lamps will remain by the end of each month.

Input

Each input will consist of a single test case.

The first line contains integers nnn and m(1≤n≤100000,1≤m≤100)m (1 \le n \le 100000, 1 \le m \le 100)m(1≤n≤100000,1≤m≤100) — the number of rooms in the Castle and the number of energy-saving lamps, which Lpl buys monthly.

The second line contains nnn integers k1,k2,...,knk_1, k_2, ..., k_nk1​,k2​,...,kn​
(1≤kj≤10000,j=1,2,...,n)(1 \le k_j \le 10000, j = 1, 2, ..., n)(1≤kj​≤10000,j=1,2,...,n) — the number of lamps in the rooms of the Castle. The number in position jjj is the number of lamps in jjj-th room. Room numbers are given in accordance with Lpl's list.

The third line contains one integer q(1≤q≤100000)q (1 \le q \le 100000)q(1≤q≤100000) — the number of queries.

The fourth line contains qqq integers d1,d2,...,dqd_1, d_2, ..., d_qd1​,d2​,...,dq​
(1≤dp≤100000,p=1,2,...,q)(1 \le d_p \le 100000, p = 1, 2, ..., q)(1≤dp​≤100000,p=1,2,...,q) — numbers of months, in which queries are formed.

Months are numbered starting with 111; at the beginning of the first month Lpl buys the first m energy-saving lamps.

Output

Print qqq lines.

Line ppp contains two integers — the number of rooms, in which all old lamps are replaced already, and the number of remaining energy-saving lamps by the end of dpd_pdp​ month.

Hint

Explanation for the sample:

In the first month, he bought 444 energy-saving lamps and he replaced the first room in his list and remove it. And then he had 111 energy-saving lamps and skipped all rooms next. So, the answer for the first month is 1,1−−−−−−11,1------11,1−−−−−−1 room's lamps were replaced already, 111 energy-saving lamp remain.

样例输入

5 4
3 10 5 2 7
10
5 1 4 8 7 2 3 6 4 7

样例输出

4 0
1 1
3 6
5 1
5 1
2 0
3 2
4 4
3 6
5 1

Solution

yy了一个树套树的做法，可是要是比赛是不可能打的
这题就是一个简单的维护区间最小值的线段树，以此来找到第一个
小于某个数的位置

CODE:

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#define ll long long
#define maxn 100005
ll n,m,ans[maxn],sum,num[maxn];
ll a[maxn*4],maxs[maxn*4];
void build(int id,int l,int r)
{
    int m;
    if(l==r)
    {
        maxs[id]=a[l];
        return ;
    }
    m=(l+r)/2;
    build(id<<1,l,m);
    build((id<<1)+1,m+1,r);
    maxs[id]=min(maxs[id*2],maxs[id*2+1]);
}
void updata(int x,ll y,int l,int r,int id)
{
    if(l==r)
    {
        maxs[id]=y;
        return;
    }
    int m=(l+r)/2;
    if(x<=m)
        updata(x,y,l,m,id*2);
    else
        updata(x,y,m+1,r,id*2+1);
    maxs[id]=min(maxs[id*2],maxs[id*2+1]);
}
int query(int id,int L, int R,int x)
{
    int ret;
    if(L==R)
    {
        if(ans[x]>=maxs[id])
        {
            num[x]++;
            ans[x]+=-maxs[id];
            updata(L,10000000000ll,1,n,1);
            return L;
        }
        return 0;
    }
    int m=(L+R)/2;
    if(maxs[id*2]<=ans[x])
        ret=query(id<<1,L,m,x);
    else
        ret=query((id<<1)+1,m+1,R,x);
    return ret;
}
void work(int x)
{
    int res,flag=0;
    num[x]=num[x-1];
    ans[x]=ans[x-1]+m;
    while(query(1,1,n,x)>0);//注意这里
}
int main(void)
{
    int q,x;
    scanf("%lld%lld",&n,&m);
    for(int i=1; i<=n; i++)
        scanf("%lld",&a[i]);
    build(1,1,n);
    sum=m;
    for(int i=1; i<=100000; i++)
    {
        if(num[i-1]==n)
        {
            num[i]=num[i-1];
            ans[i]=ans[i-1];
            continue;
        }
        work(i);
        //sum=ans[i]+m;
    }
    scanf("%d",&q);
    for(int i=1; i<=q; i++)
        scanf("%d",&x),printf("%lld %lld\n",num[x],ans[x]);
    return 0;
}

 

---

---

---

K. The Great Nim Game

Nim is a famous game as you know. Nim is a 222-player game featuring several piles of stones. Players alternate turns, and on his/her turn, a player's move consists of removing one or more stones from any single pile. Play ends when all the stones have been removed. The first player who can't remove is declared as the loser.

Now you want to play the Great Nim Game. In the other words, you want to choose several (0(0(0 ~ N)N)N) pile(s) from NNN piles of stones. You want know how many choices you have making sure that the first player must win. They both try their best (optimal strategy) to win through the game.

Input

The first line contains two numbers N x1N\ x_1N x1​, denoting the number of piles and the number of stones in the first pile.

The second line contains five integers a,b,c,d,ea, b, c, d, ea,b,c,d,e.

The third line contains one integer kkk, denoting a function

f(x)=f(x)=f(x)=
(ax4+bx3+cx2+dx1+e−1)%k+1(ax^4+bx^3+cx^2+dx^1+e - 1)\%k+1(ax4+bx3+cx2+dx1+e−1)%k+1.

With these, you can figure out the number of stones in the iii-th pile xi=f(xi−1)(1<i≤N)x_i = f(x_{i-1}) (1<i\le N)xi​=f(xi−1​)(1<i≤N)

It is guaranteed that

1<N<10100000001<N<10^{10000000}1<N<1010000000,
0<x1≤k,0≤a,b,c,d,e<2120<x_1\le k, 0\le a, b, c, d,e<2^{12}0<x1​≤k,0≤a,b,c,d,e<212,
a+b+c+d+e>0,0<k<212a+ b+ c+ d+ e>0, 0<k<2^{12}a+b+c+d+e>0,0<k<212.

Output

Print the number of solutions making sure the first player must win. The answer may be very large, so you should output it mod 1e9+7(1e9+7 (% 1000000007)1e9+7(.

Hint

In the first sample, there are 1,2,3,4,51, 2, 3, 4, 51,2,3,4,5 stones in the 111-st, 222-nd, 333th, 444th, 555th pile. You can figure out there are exactly 444 choosing ({1,2,3}{1,4,5}{2,3,4,5}{}(\lbrace 1, 2, 3 \rbrace \lbrace 1,4,5 \rbrace \lbrace 2,3,4,5 \rbrace \lbrace \rbrace({1,2,3}{1,4,5}{2,3,4,5}{}(empty, you choose zero pile)) ways that make first-hand player must lose, so the answer is 25−4=282^5-4=2825−4=28.

If xxx is in range (1≤x≤k),f(x)(1\le x\le k), f(x)(1≤x≤k),f(x) must be in range (1≤f(x)≤k)(1\le f(x)\le k)(1≤f(x)≤k), too.

样例输入1

5 1
0 0 0 1 1
16

样例输出1

28

样例输入2

100000000000000000000 1
0 0 0 1 1
4095

样例输出2

394326889

样例输入3

100000000000000000000 1
1 0 0 1 1
4095

样例输出3

933180537

 solution:

可以看出，最坏情况下，这里总共只会有K+1个数字。所以不用害怕可以选择的数字太多。注意到我要求的是异或和为0的方案数，异或和我们容易想到用线性基求解。对于这个N个数字，实际最多K+1种数字，我们建立线性基，不妨设这个基的基底数量为x。根据线性基的性质，所有的数字一定可以表示为这x个数字的线性组合。因此，除了这x个数字外，在其余数字种任意选取几个，它们的异或和也一定能够分解为这x个数字的线性组合，这是因为异或运算具有封闭性。然后在线性基下，可以选择的系数也只有0和1。也就意味着，N-x个数字种，选择任意一个子集，设它们的异或和为sum，那么我一定也能够在x个线性基的基底中找到一个子集，使得它们的异或和也为sum，这样两个集合的数字再异或起来，结果就是0，对应先手必败的方案。N-x个数字的自己个数是2^(N-x)，所以这就是先手必败的方案。那么最后的答案就是：

   ans=2^N-2^{N-x}

code:

#include<bits/stdc++.h>
#define mod 1000000007
#define LL long long
#define pb push_back
#define lb lower_bound
#define ub upper_bound
#define INF 0x3f3f3f3f
#define sf(x) scanf("%lld",&x)
#define sc(x,y,z) scanf("%lld%lld%lld",&x,&y,&z)
using namespace std;
 
struct Linear_Basis
{
    LL b[14],tot;
    void init(){memset(b,0,sizeof(b));tot=0;}
 
    bool ins(LL x)
    {
        for(int i=13;i>=0;i--)
            if (x&(1<<i))
            {
                if (!b[i]) {b[i]=x;tot++;break;}
                x^=b[i];
            }
        return x>0;
    }
 
} LB;
 
LL a,b,c,d,e,n,x,k;
char s[10000010];
bool v[4100];
 
LL qpow(LL x,LL n)
{
    LL res=1;
    n=(n+mod-1)%(mod-1);
    while(n)
    {
        if (n&1) res=res*x%mod;
        n>>=1; x=x*x%mod;
    }
    return res;
}
 
int main()
{
    scanf("%s",s);
    sc(x,a,b); sc(c,d,e);
 
    LL m=0; sf(k);
    for(int i=0;s[i];i++)
    {
        n=(n*10+s[i]-'0')%(mod-1);
        if (n>k) m=INF;
    }
    LL ans=qpow(2,n);
    LB.init(); if (m==0) m=n;
    while(!v[x]&&m--)
    {
        v[x]=1; LB.ins(x);
        x=(a*x*x*x*x+b*x*x*x+c*x*x+d*x+e-1LL)%k+1;
    }
 
    printf("%lld\n",(ans-qpow(2,(n-LB.tot)%(mod-1)+mod-1)+mod)%mod);
    return 0;
}