【概率机器人】2 递归状态估计
为了方便后面对算法的讨论,【概率机器人】在这一章中介绍了概率的基本概念、机器人模型中的关键术语、贝叶斯滤波。本文基于这三个部分,分别记录了个人笔记和理解。
1. 概率的基本概念
这里主要是介绍了概率论的一些基本概念:离散/连续随机变量的概率密度函数、联合分布函数、条件概率、贝叶斯准则、期望、协方差。不过有以下几点需要更进一步了解:
(1) 正态分布
一维正态分布与多元正态分布的概率密度函数:
$$ p(x)=(2\pi \sigma ^2)^{-\frac{1}{2}}\exp\left \{ -\frac{1}{2} \frac{(x-\mu )^2}{\sigma ^2}\right \} \tag{2.1} $$
$$ p(\boldsymbol{x})=\det(2\pi\boldsymbol{\Sigma} )^{-\frac{1}{2}}\exp\left \{ -\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}}\boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right \} \tag{2.2} $$
式(2.1)表示均值为$\mu$、方差为$\sigma$的一维正态分布,记为$N(x;\mu,\sigma^2)$。式(2.2)表示的是多元正态分布,其变量$\boldsymbol{x}$是一个多维矢量,$\boldsymbol{\mu}$为均值矢量,$\boldsymbol{\Sigma}$为协方差矩阵,是一个半正定矩阵。对于多元正态分布,我们有以下性质需要进行说明:
(a) 概率密度函数 $p(\boldsymbol{x})$ 在均值矢量处($\boldsymbol{x}=\boldsymbol{\mu}$)取得最大值,更进一步,有
取 $L(\boldsymbol{x})=\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}}\boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})$ , 则式(2.2)可表示为$ p(\boldsymbol{x})=\det(2\pi\boldsymbol{\Sigma} )^{-\frac{1}{2}}\exp\left \{ -L(\boldsymbol{x})\right \}$。
我们再分析一下 $L(\boldsymbol{x})$,其实它是一个二次型,并且它对 $\boldsymbol{x}$的一、二阶导数为:
$$ \frac{\partial L(\boldsymbol{x})}{\partial \boldsymbol{x}} = \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu}), \, \frac{\partial^2 L(\boldsymbol{x})}{\partial \boldsymbol{x^2}} = \boldsymbol{\Sigma}^{-1} \tag{2.3} $$
从这里,我们可以发现, $L(\boldsymbol{x})$在$\boldsymbol{x}=\boldsymbol{\mu}$处取得最小值,且其对 $\boldsymbol{x}$的二阶导数正好是$\boldsymbol{\Sigma}^{-1}$,这一点在卡尔曼滤波的数字推导中会被使用到。
(2) 归一化变量
在本书中,对于不依赖于概率变量的系数项,会适当使用归一化变量 $\eta$ 进行简化。例如:贝叶斯准则中,有
$$ p(x|y)=\frac{p(x)p(y|x)}{p(y)} \tag{2.4} $$
这里的分母$p(y)$并不依赖概率变量$x$,因此通常将式(2.4)写为
$$ p(x|y)=\eta p(x)p(y|x) \tag{2.5} $$
• 注意:在不同公式中将自由地用同一个$\eta$来表示归一化,即使它们的实际值是可能不相等的。
(3)条件独立
在满足条件$z$时,$x$、$y$相互独立,则称$x$、$y$是条件独立事件。即
$$p(x,y|z)=p(x|z)p(y|z) \tag{2.6}$$
其等价于
$$p(x|z)=p(x|z,y),p(y|z)=p(y|z,x) \tag{2.7}$$
• 注意:条件独立并不意味着(绝对)独立。
(4) 熵
一个概率分布的熵有下式给出:
$$H_p(x)=E[-log_2p(x)] \tag{2.8}$$
根据离散分布和连续分布,可分别导出:
$$H_p(x)=-\sum_xp(x)log_2p(x){(离散)},H_p(x)=-\int p(x)log_2p(x) \mathrm{d}x {(连续)}. \tag{2.9}$$
2. 机器人模型中的关键术语
机器人在执行任务时是需要不断与环境进行交互,即使用各种传感器来获取周围环境的状态和机器人自身的运动状态。但是,传感器是有噪声的,会存在测量误差,并且也会有许多信息无法通过传感器直接测量。对于这些情况,我们都会采用的机器人模型和观测模型来获得更接近真实的信息。这一节主要介绍一些概率机器人中用于描述机器人运动状态和环境状态的相关术语。
(1) 状态
状态用 $\mathbf{x}$表示,用于描述会对未来产生影响的机器人自身运行状态和环境特征。时间 $t$ 的状态表示为 $\mathbf{x}_t$,从时间 $t_1$ 到 $t_2$ 的状态表示为 $\mathbf{x}_{t_1:t_2}(=\mathbf{x}_{t_1},\mathbf{x}_{t_1+1},...,\mathbf{x}_{t_2}) $.
如果一个状态 $\mathbf{x}_t$ 可以最好地预测未来,则称其为完整的。换句话说,完整性包括过去状态测量及控制的信息,这一点对于构成马尔可夫链非常重要。
(2)测量值
获取环境特征和机器人自身运行状态需要通过传感器的来完成,而一般传感器获得的数据是真实状态与测量噪声的叠加,由此,用 $\mathbf{z}$ 表示测量值。
时间 $t$ 的状态表示为 $\mathbf{z}_t$,从时间 $t_1$ 到 $t_2$ 的状态表示为 $\mathbf{z}_{t_1:t_2}(=\mathbf{z}_{t_1},\mathbf{z}_{t_1+1},...,\mathbf{z}_{t_2}) $.
(3) 控制动作(控制)
根据当前的所有信息,机器人所作出的控制行为,用 $\mathbf{u}$ 表示。
类似的,时间 $t$ 的状态表示为 $\mathbf{u}_t$,从时间 $t_1$ 到 $t_2$ 的状态表示为 $\mathbf{u}_{t_1:t_2}(=\mathbf{u}_{t_1},\mathbf{u}_{t_1+1},...,\mathbf{u}_{t_2} )$.
(4) 概率生成法则
概率机器人中,会使用概率分布来表示状态、测量值的取值。具体而言,在时刻$t$时,其状态 $\mathbf{x}_t$ 与过去的信息(测量值 $\mathbf{z}_{1:t-1}$ 、状态$\mathbf{x}_{0:t-1}$和控制动作$\mathbf{u}_{1:t}$)有关,可以写成条件概率的形式:
$$ p(\mathbf{x}_t | \mathbf{x}_{0:t-1}, \mathbf{z}_{1:t-1}, \mathbf{u}_{1:t}) \tag{2.10} $$
类似的,由于测量存在噪声等,对于测量过程也可以建立概率模型:
$$ p(\mathbf{z}_t | \mathbf{x}_{0:t}, \mathbf{z}_{1:t-1}, \mathbf{u}_{1:t}) \tag{2.11} $$
如果状态 $\mathbf{x}$ 是完整的,那么它是所有以前时刻发生的所有状态的充分总结。具体来说,当确定$\mathbf{x}_{t-1}$时,$\mathbf{u}_{1:t-1}$和$\mathbf{z}_{1:t-1}$的值不会影响后面时刻的统计分析。用概率术语表示,即
$$ p(\mathbf{x}_t | \mathbf{x}_{0:t-1}, \mathbf{z}_{1:t-1}, \mathbf{u}_{1:t}) = p(\mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{u}_t) \tag{2.12} $$
$$ p(\mathbf{z}_t | \mathbf{x}_{0:t}, \mathbf{z}_{1:t-1}, \mathbf{u}_{1:t}) = p(\mathbf{z}_t | \mathbf{x}_t) \tag{2.13} $$
这两个等式的特性就是条件独立。它表示“当确定第三组变量($\mathbf{x}_{t-1}$)的值时,概率变量独立于其他变量($\mathbf{u}_{1:t-1}$和$\mathbf{z}_{1:t-1}$)”。
• 特别的,概率 $p(\mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{u}_t) $ 被称为状态转移概率,它指出环境状态的变化与机器人控制动作的关系;概率 $p(\mathbf{z}_t | \mathbf{x}_t)$ 被称为测量概率,它描述了测量值与状态之间的关系。状态转移概率和测量概率一起描述机器人及其环境组成的动态随机系统,随着时间 $t$ 的推进,我们可以用图2-1 来表示这一演变过程,这样的时间生成模型也称为隐马尔可夫模型。
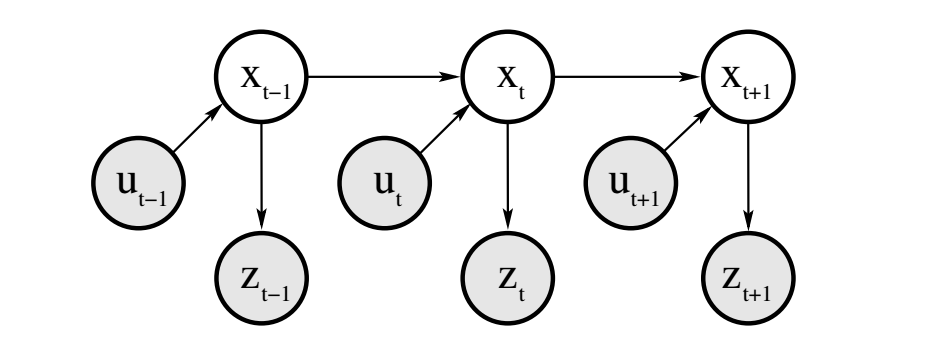
图2-1 表征“控制、状态和测量”演变特征的动态贝叶斯网络
(5) 置信分布
由于观测过程存在噪声,因此对于真实的状态,我们始终是无法精确获取,只能根据观测值来估计状态。在概率机器人中,使用置信度来描述状态的最优估计,具体而言,置信度分布为每一个可能的状态分配了一个概率(或者概率密度值)。
用 $\mathrm{bel} (\mathbf{x}_t)$表示状态 $\mathbf{x}_t$的置信度,是根据测量值 $\mathbf{z}_{1:t}$和控制 $\mathbf{u}_{1:t}$来推测,即:
$$ \mathrm{bel}(\mathbf{x}_t) = p(\mathbf{x}_t | \mathbf{z}_{1:t},\mathbf{u}_{1:t}) \tag{2.14} $$
可以发现,以上置信度是在综合$t$时刻的观测值 $\mathbf{z}_t$后得到的。另外,当我们在执行控制 $\mathbf{u}_t$时,对 $x_t$来进行推测,即:
$$ \overline{\mathrm{bel}}(\mathbf{x}_t) = p(\mathbf{x}_t | \mathbf{z}_{1:t-1},\mathbf{u}_{1:t}) \tag{2.15} $$
在概率滤波框架下,式(2.15)被称为预测,式(2.14)被称为修正或测量更新。根据$t$时刻的观测值 $\mathbf{z}_t$ 来修正预测值 $\overline{\mathrm{bel}}(\mathbf{x}_t) $,获得状态 $\mathbf{x}_t$的最优估计 $ \mathrm{bel}(\mathbf{x}_t)$。
3. 贝叶斯滤波
(1) 贝叶斯滤波算法
贝叶斯滤波算法是根据已有的测量和控制数据,来估计状态变量 $\mathbf{x}_t$ ,具体而言,就是计算状态变量 $\mathbf{x}_t$ 的置信度 $ \mathrm{bel}(\mathbf{x}_t)$ 。
时刻 $t$ 的置信度 $ \mathrm{bel}(\mathbf{x}_t)$ 由式(2.14)给出,但这样计算过于复杂,因此贝叶斯滤波提供一种递归求解方式,即根据 $ \mathrm{bel}(\mathbf{x}_{t-1})$ 计算 $ \mathrm{bel}(\mathbf{x}_t)$。程序[2.1]给出了贝叶斯滤波算法的一次迭代过程。
| 程序 2.1 基本的贝叶斯滤波算法 | |
| 1: | Algorithm Bayes_filter( $ \mathrm{bel}(\mathbf{x}_{t-1})$, $\mathbf{u}_t$, $\mathbf{z}_t$ ) |
| 2: | for all $x_t$ do |
| 3: | $\overline{\mathrm{bel}}(x_t) = \int p(x_t | u_t, x_{t-1}) \mathrm{bel}(x_{t-1}) \mathrm{d}x_{t-1} $ |
| 4: | $ \mathrm{bel}(x_t) = \eta p(z_t | x_t) \overline{\mathrm{bel}}(x_t) $ |
| 5: | endfor |
| 6: | return $ \mathrm{bel}(\mathbf{x}_t)$ |
程序2.1的贝叶斯滤波算法主要分为两个步骤:预测、测量更新。预测为程序的第3行,测量更新为程序的第4行。
(a)预测:即程序的第3行,预测阶段是求解 $ \overline{\mathrm{bel}}(\mathbf{x}_t) $ ,其定义由式(2.15)给出。基于状态 $\mathbf{x}_{t-1}$ 的置信度和控制 $\mathbf{u}_t$ 来计算状态 $\mathbf{x}_{t}$ 的置信度。
(b)测量更新:在得到观测值 $\mathbf{z}_t$ 后,可以进一步修正 $\mathbf{x}_{t}$ 的置信度,得到 $ \mathrm{bel}(\mathbf{x}_t)$。
在使用贝叶斯滤波算法时,需要预先实现三个概率分布:初始置信度 $ \mathrm{bel}(\mathbf{x}_0) = p(\mathbf{x}_0) $,测量概率 $p(\mathbf{z}_t | \mathbf{x}_t)$ 和状态转移概率 $p(\mathbf{x}_t | \mathbf{u}_t, \mathbf{x}_{t-1})$。在概率机器人中,第5、6章将分别介绍状态转移概率与测量概率的实现过程,而初始置信度根据实际项目进行自行设置即可。
(2) 贝叶斯滤波算法的数学推导
首先,需要假设 $\mathbf{x}_{t}$ 是完整的,即式(2.16)(2.17)成立:
$$ p(\mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{z}_{1:t-1}, \mathbf{u}_{1:t}) = p(\mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{u}_t) \tag{2.16} $$
$$ p(\mathbf{z}_t | \mathbf{x}_{t}, \mathbf{z}_{1:t-1}, \mathbf{u}_{1:t}) = p(\mathbf{z}_t | \mathbf{x}_t) \tag{2.17} $$
这两个式子与(2.12)(2.13)只有一点点差别。
(a) 预测:
预测阶段是利用 $ \mathrm{bel}(\mathbf{x}_{t-1})$ 计算 $ \overline{\mathrm{bel}}(\mathbf{x}_t)$,根据式(2.15),可得
$$ \begin{align*} \overline{\mathrm{bel}}(\mathbf{x}_t) &= p(\mathbf{x}_t | \mathbf{z}_{1:t-1},\mathbf{u}_{1:t}) \\ &= \int p(\mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{z}_{1:t-1},\mathbf{u}_{1:t}) p(\mathbf{x}_{t-1} | \mathbf{z}_{1:t-1},\mathbf{u}_{1:t}) \mathrm{d}\mathbf{x}_{t-1} \end{align*} \tag{2.18}$$
利用式(2.16)和式(2.14),可得
$$ \overline{\mathrm{bel}}(\mathbf{x}_t) = \int p(\mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{u}_t) \mathrm{bel}(\mathbf{x}_{t-1}) \mathrm{d}\mathbf{x}_{t-1} \tag{2.19} $$
正好对应程序2.1的第三行。
(b) 测量更新:
测量更新阶段是利用测量值 $\mathbf{z}_t$ 和 $ \overline{\mathrm{bel}}(\mathbf{x}_t)$ 计算 $ \mathrm{bel}(\mathbf{x}_{t})$。根据式(2.14),可得
$$ \begin{align*} \mathrm{bel}(\mathbf{x}_t) &= p(\mathbf{x}_t | \mathbf{z}_{1:t},\mathbf{u}_{1:t}) \\ &=\frac{ p(\mathbf{z}_t | \mathbf{x}_t, \mathbf{z}_{1:t-1}, \mathbf{u}_{1:t}) p(\mathbf{x}_t |\mathbf{z}_{1:t-1}, \mathbf{u}_{1:t}) }{ p(\mathbf{z}_t | \mathbf{z}_{1:t-1}, \mathbf{u}_{1:t}) } \\ &= \eta p(\mathbf{z}_t | \mathbf{x}_t, \mathbf{z}_{1:t-1}, \mathbf{u}_{1:t}) p(\mathbf{x}_t |\mathbf{z}_{1:t-1}, \mathbf{u}_{1:t}) \end{align*} \tag{2.20} $$
再利用式(2.17)和式(2.15),可得
$$ \mathrm{bel}(\mathbf{x}_t) = \eta p(\mathbf{z}_t | \mathbf{x}_t) \overline{\mathrm{bel}}(\mathbf{x}_t) \tag{2.21} $$
正好对应程序2.1的第4行 ,证毕。□



