Codeforces 932.E Team Work

E. Team Work

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You have a team of N people. For a particular task, you can pick any non-empty subset of people. The cost of having x people for the task is xk.

Output the sum of costs over all non-empty subsets of people.

Input

Only line of input contains two integers N (1 ≤ N ≤ 109) representing total number of people and k (1 ≤ k ≤ 5000).

Output

Output the sum of costs for all non empty subsets modulo 109 + 7.

Examples

input

1 1

output

1

input

3 2

output

24

Note

In the first example, there is only one non-empty subset {1} with cost 11 = 1.

In the second example, there are seven non-empty subsets.

- {1} with cost 12 = 1

- {2} with cost 12 = 1

- {1, 2} with cost 22 = 4

- {3} with cost 12 = 1

- {1, 3} with cost 22 = 4

- {2, 3} with cost 22 = 4

- {1, 2, 3} with cost 32 = 9

The total cost is 1 + 1 + 4 + 1 + 4 + 4 + 9 = 24.

题目大意：求.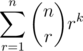

分析：挺难的一道题，完全下不了手......

　　　官方题解给出的做法非常巧妙.首先这个式子一眼看上去肯定不能直接解.变换一下？不会. 可以想到一个比较相似的式子：.

　　　那么怎么把这个式子变成题目给的式子呢？找一找不同，要求的式子r是从1开始的，这个式子r是从0开始的; 要求的式子r作为底数，k作为幂次，而这个式子凭空出现了一个x.变换比较难想到：

可以把这个式子求个导，然后乘x.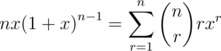 

　　　　求导可以将x的幂次中的r提出来一个，同时r=0时求导就变成了0.那么操作k次就能得到和要求的式子差不多的一个式子.有什么差别呢？式子中有x.

　　　消除掉x的影响就可以了，想办法令x的幂次为1.可以利用dp.设f[a][b][c]表示还剩a次操作，式子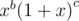的值.如果b=0,c = n,同时令x = 1,那么这个式子操作k次后正好就是要求的式子.对这个式子操作一次，变成了：，那么可以得到递推式：f[a][b][c] = b * f[a - 1][b][c] + c * f[a - 1][b + 1][c - 1].，最后答案是f[k][0][n].

　　　看似是三次复杂度的dp,实际上是平方级别的，因为b和c的和一定等于n.那么dp只需要记录a和b的状态,c可以推出来. (不能记录c，因为c可能高达n,而实际上b和c最多只会变化k,b是从0开始的，所以记录b).

　　　代码中的a,b表示上述分析中的b,c，一定要考虑边界情况：b = 0或c = 0,当a = 0时，就是一些连续的组合数相加，因为中的x = 1，直接返回2^c.

 

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;

const ll mod = 1e9+7;

ll n,k,f[5010][5010];

ll qpow(ll a,ll b)
{
    ll res = 1;
    while (b)
    {
        if (b & 1)
            res = (res * a) % mod;
        a = (a * a) % mod;
        b >>= 1;
    }
    return res % mod;
}

ll dfs(ll dep,ll a)
{
    if (f[dep][a] >= 0)
        return f[dep][a];
    ll b = n - a;
    if (dep == 0)
        return f[dep][a] = qpow(2,b);
    return f[dep][a] = ((b?1LL*b*dfs(dep-1,a+1):0LL)+(a?1LL*a*dfs(dep-1,a):0LL))%mod;
}

int main()
{
    memset(f,-1,sizeof(f));
    cin >> n >> k;
    cout << dfs(k,0) % mod << endl;

    return 0;
}