Codeforces 932.D Tree
You are given a node of the tree with index 1 and with weight 0. Let cnt be the number of nodes in the tree at any instant (initially, cnt is set to 1). Support Q queries of following two types:
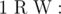Add a new node (index cnt + 1) with weight W and add edge between node R and this node.
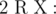Output the maximum length of sequence of nodes which- starts with R.
- Every node in the sequence is an ancestor of its predecessor.
- Sum of weight of nodes in sequence does not exceed X.
- For some nodes i, j that are consecutive in the sequence if i is an ancestor of j then w[i] ≥ w[j] and there should not exist a node k on simple path from i to j such that w[k] ≥ w[j]
The tree is rooted at node 1 at any instant.
Note that the queries are given in a modified way.
First line containing the number of queries Q (1 ≤ Q ≤ 400000).
Let last be the answer for previous query of type 2 (initially last equals 0).
Each of the next Q lines contains a query of following form:
- 1 p q (1 ≤ p, q ≤ 1018): This is query of first type where
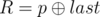and 
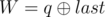. It is guaranteed that 1 ≤ R ≤ cnt and0 ≤ W ≤ 109. - 2 p q (1 ≤ p, q ≤ 1018): This is query of second type where 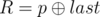and
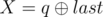. It is guaranteed that 1 ≤ R ≤ cntand 0 ≤ X ≤ 1015.
denotes bitwise XOR of a and b.
It is guaranteed that at least one query of type 2 exists.
Output the answer to each query of second type in separate line.
6
1 1 1
2 2 0
2 2 1
1 3 0
2 2 0
2 2 2
0
1
1
2
6
1 1 0
2 2 0
2 0 3
1 0 2
2 1 3
2 1 6
2
2
3
2
7
1 1 2
1 2 3
2 3 3
1 0 0
1 5 1
2 5 0
2 4 0
1
1
2
7
1 1 3
1 2 3
2 3 4
1 2 0
1 5 3
2 5 5
2 7 22
1
2
3
In the first example,
last = 0
- Query 1: 1 1 1, Node 2 with weight 1 is added to node 1.
- Query 2: 2 2 0, No sequence of nodes starting at 2 has weight less than or equal to 0. last = 0
- Query 3: 2 2 1, Answer is 1 as sequence will be {2}. last = 1
- Query 4: 1 2 1, Node 3 with weight 1 is added to node 2.
- Query 5: 2 3 1, Answer is 1 as sequence will be {3}. Node 2 cannot be added as sum of weights cannot be greater than 1. last = 1
- Query 6: 2 3 3, Answer is 2 as sequence will be {3, 2}. last = 2
题目大意：一棵树,每个点有点权，两种操作：1.新加一个点连接r,权值为w. 2.从一个点r开始往祖先上跳，每次跳到第一个值≥自身的祖先，将跳到的点的和加起来，不能大于w,问能跳几次.
分析：挺有意思的一道题.
暴力算法就是一个一个往上跳着找喽，在树上往上跳有一种常用的优化方法--倍增.在这道题里面可以倍增地跳到≥自身权值的点.
考虑怎么实现，fa数组就不能记录第2^i个祖先了，而要记录比自身权值大的第2^i个祖先.在加点的时候处理.可以发现，一旦处理出fa[i][0],就能够根据祖先节点的信息推出fa[i][j].
如何处理fa[i][0]?如果r的权值比新加的点i的权值大或相等，则fa[i][0] = r，否则从r开始往上跳，如果w[fa[r][j]] < w[i],则往上跳，最后fa[i][0] = fa[r][0].
因为最后要求和嘛，可以顺便维护一个sum数组，表示从i这个点跳到比i权值大的第2^j个祖先跳到的点的权值和为多少. 求出了这两个数组以后查询就很好办了，sum[i][j]是否≤w,是的话就往上跳，并且w -= sum[i][j].倍增的基础应用嘛.
想清楚如何加速往祖先跳的过程，以及倍增应该维护什么东西这道题就能解决了.
一些边界的值需要特殊考虑！
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; const ll maxn = 400010,inf = 1e18; ll q,lastans,cnt = 1,w[maxn]; ll fa[maxn][21],sum[maxn][21]; void add(ll x,ll v) { w[++cnt] = v; if (w[cnt] <= w[x]) fa[cnt][0] = x; else { int y = x; for (int i = 20; i >= 0; i--) { if (w[fa[y][i]] < w[cnt]) y = fa[y][i]; } fa[cnt][0] = fa[y][0]; } if (fa[cnt][0] == 0) sum[cnt][0] = inf; else sum[cnt][0] = w[fa[cnt][0]]; for (int i = 1; i <= 20; i++) { fa[cnt][i] = fa[fa[cnt][i - 1]][i - 1]; if (fa[cnt][i] == 0) sum[cnt][i] = inf; else sum[cnt][i] = sum[cnt][i - 1] + sum[fa[cnt][i - 1]][i - 1]; } } ll query(ll x,ll v) { if (w[x] > v) return 0; v -= w[x]; ll res = 1; for (int i = 20; i >= 0; i--) { if (v >= sum[x][i]) { v -= sum[x][i]; res += (1 << i); x = fa[x][i]; } } return res; } int main() { w[0] = inf; for (int i = 0; i <= 20; i++) sum[1][i] = inf; scanf("%I64d",&q); while (q--) { int id; ll a,b; scanf("%d",&id); scanf("%I64d%I64d",&a,&b); a ^= lastans; b ^= lastans; if (id == 1) add(a,b); else printf("%I64d\n",lastans = query(a,b)); } }
