Codeforces 717.F Heroes of Making Magic III
I’m strolling on sunshine, yeah-ah! And doesn’t it feel good! Well, it certainly feels good for our Heroes of Making Magic, who are casually walking on a one-directional road, fighting imps. Imps are weak and feeble creatures and they are not good at much. However, Heroes enjoy fighting them. For fun, if nothing else.
Our Hero, Ignatius, simply adores imps. He is observing a line of imps, represented as a zero-indexed array of integers a of length n, where ai denotes the number of imps at the i-th position. Sometimes, imps can appear out of nowhere. When heroes fight imps, they select a segment of the line, start at one end of the segment, and finish on the other end, without ever exiting the segment. They can move exactly one cell left or right from their current position and when they do so, they defeat one imp on the cell that they moved to, so, the number of imps on that cell decreases by one. This also applies when heroes appear at one end of the segment, at the beginning of their walk.
Their goal is to defeat all imps on the segment, without ever moving to an empty cell in it (without imps), since they would get bored. Since Ignatius loves imps, he doesn’t really want to fight them, so no imps are harmed during the events of this task. However, he would like you to tell him whether it would be possible for him to clear a certain segment of imps in the above mentioned way if he wanted to.
You are given q queries, which have two types:
- 1 a b k — denotes that k imps appear at each cell from the interval [a, b]
- 2 a b - asks whether Ignatius could defeat all imps on the interval [a, b] in the way described above
The first line contains a single integer n (1 ≤ n ≤ 200 000), the length of the array a. The following line contains n integers a1, a2, ..., an(0 ≤ ai ≤ 5 000), the initial number of imps in each cell. The third line contains a single integer q (1 ≤ q ≤ 300 000), the number of queries. The remaining q lines contain one query each. Each query is provided by integers a, b and, possibly, k (0 ≤ a ≤ b < n, 0 ≤ k ≤ 5 000).
For each second type of query output 1 if it is possible to clear the segment, and 0 if it is not.
3
2 2 2
3
2 0 2
1 1 1 1
2 0 2
0
1
For the first query, one can easily check that it is indeed impossible to get from the first to the last cell while clearing everything. After we add 1 to the second position, we can clear the segment, for example by moving in the following way: 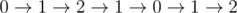
题目大意:给一个区间,有两种操作:1.将[a,b]所有的数+k. 2.询问能不能将[a,b]中的数减完.规则是:每经过一个数,这个数就会-1,不能经过为0的数,并且每次只能左移或右移一格.
分析:比较难的一道题.
关键是要想到第二种操作的方案.构造出方案就好做了.可以从最左端点走,每次将当前位置变成0,方法就是不断的在当前位置和下一位置走.这样的话需要满足条件:a(i + 1) >= ai,走到点i+1后,a(i + 1)就变成了a(i + 1) - ai,对于a(i + 1)和a(i + 2)有同样的条件.那么到最后需要满足的条件就是
ar−a(r−1)+⋯≥[(r−a+1)≡1(mod2)]这里的r是区间[a,b]的任意一个数,并且ab - a(b - 1) + ...... = (b - a + 1) mod 2.
考虑如何实现,因为第一个条件有大于等于号,并且r是区间的任意一个数,那么只需要维护一下最小值就可以了,记d = ai - a(i-1) + a(i - 2)......在线段树上维护d.注意到d中ai的系数是正数还是负数取决于维护的两个端点的奇偶性,在修改和查询的时候要对奇偶性进行分类讨论.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int maxn = 200010,inf = 1e9; int n,m,a[maxn],b[maxn],minn[maxn << 2][2],tag[maxn << 2][2]; void pushup(int o) { minn[o][0] = min(minn[o * 2][0],minn[o * 2 + 1][0]); minn[o][1] = min(minn[o * 2][1],minn[o * 2 + 1][1]); } void pushdown(int o) { for (int i = 0; i < 2; i++) { if (tag[o][i]) { minn[o * 2][i] += tag[o][i]; minn[o * 2 + 1][i] += tag[o][i]; tag[o * 2][i] += tag[o][i]; tag[o * 2 + 1][i] += tag[o][i]; tag[o][i] = 0; } } } void build(int o,int l,int r) { if (l == r) { minn[o][l & 1] = b[l]; minn[o][l & 1 ^ 1] = inf; return; } int mid = (l + r) >> 1; build(o * 2,l,mid); build(o * 2 + 1,mid + 1,r); pushup(o); } void update(int o,int l,int r,int x,int y,int v,int id) { if (x > y) return; if(x <= l && r <= y) { tag[o][id] += v; minn[o][id] += v; return; } pushdown(o); int mid = (l + r) >> 1; if (x <= mid) update(o * 2,l,mid,x,y,v,id); if (y > mid) update(o * 2 + 1,mid + 1,r,x,y,v,id); pushup(o); } int query1(int o,int l,int r,int cur,int id) { if (cur == 0) //易错 return 0; if (l == r) return minn[o][id]; pushdown(o); int mid = (l + r) >> 1; if (cur <= mid) return query1(o * 2,l,mid,cur,id); if (cur > mid) return query1(o * 2 + 1,mid + 1,r,cur,id); } int query2(int o,int l,int r,int x,int y,int id) { if (x <= l && r <= y) return minn[o][id]; pushdown(o); int mid = (l + r) >> 1,res = inf; if (x <= mid) res = min(res,query2(o * 2,l,mid,x,y,id)); if (y > mid) res = min(res,query2(o * 2 + 1,mid + 1,r,x,y,id)); return res; } int main() { scanf("%d",&n); for (int i = 1; i <= n; i++) scanf("%d",&a[i]); for (int i = 1; i <= n; i++) b[i] = a[i] - b[i - 1]; //维护的就是d build(1,1,n); scanf("%d",&m); for (int i = 1; i <= m; i++) { int id,a,b,k; scanf("%d",&id); if (id == 1) { scanf("%d%d%d",&a,&b,&k); a++; b++; update(1,1,n,a,b,k,a & 1); if ((b - a + 1) & 1) //如果区间长度是偶数的话,+-抵消了 { update(1,1,n,b + 1,n,k,a & 1); //b维护的是类似前缀和一样的东西,所以要对区间右边的操作. update(1,1,n,b + 1,n,-k,a & 1 ^ 1); //这里+k,-k主要取决于有影响的数在之后的区间的系数. } } else { scanf("%d%d",&a,&b); a++; b++; if ((b - a + 1) & 1) { int temp1 = query1(1,1,n,a - 1,(a - 1) & 1); //这里的四个temp就是利用b数组类似前缀和的一个特点得到的. int temp2 = query2(1,1,n,a,b,b & 1) + temp1; int temp3 = query2(1,1,n,a,b,b & 1 ^ 1) - temp1; int temp4 = query1(1,1,n,b,b & 1) + temp1; if (temp4 == 1 && temp2 >= 1 && temp3 >= 0) puts("1"); else puts("0"); } else { int temp1 = query1(1,1,n,a - 1,(a - 1) & 1); int temp2 = query2(1,1,n,a,b,b & 1) - temp1; int temp3 = query2(1,1,n,a,b,b & 1 ^ 1) + temp1; int temp4 = query1(1,1,n,b,b & 1) - temp1; if (temp4 == 0 && temp2 >= 0 &&temp3 >= 1) puts("1"); else puts("0"); } } } return 0; }



