noip2016 愤怒的小鸟
题目描述
Kiana最近沉迷于一款神奇的游戏无法自拔。
简单来说,这款游戏是在一个平面上进行的。
有一架弹弓位于(0,0)处,每次Kiana可以用它向第一象限发射一只红色的小鸟,小鸟们的飞行轨迹均为形如的曲线,其中a,b是Kiana指定的参数,且必须满足a<0。
当小鸟落回地面(即x轴)时,它就会瞬间消失。
在游戏的某个关卡里,平面的第一象限中有n只绿色的小猪,其中第i只小猪所在的坐标为(xi,yi)。
如果某只小鸟的飞行轨迹经过了(xi,yi),那么第i只小猪就会被消灭掉,同时小鸟将会沿着原先的轨迹继续飞行;
如果一只小鸟的飞行轨迹没有经过(xi,yi),那么这只小鸟飞行的全过程就不会对第i只小猪产生任何影响。
例如,若两只小猪分别位于(1,3)和(3,3),Kiana可以选择发射一只飞行轨迹为的小鸟,这样两只小猪就会被这只小鸟一起消灭。
而这个游戏的目的,就是通过发射小鸟消灭所有的小猪。
这款神奇游戏的每个关卡对Kiana来说都很难,所以Kiana还输入了一些神秘的指令,使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。
假设这款游戏一共有T个关卡,现在Kiana想知道,对于每一个关卡,至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算,所以希望由你告诉她。
输入输出格式
输入格式:
第一行包含一个正整数T,表示游戏的关卡总数。
下面依次输入这T个关卡的信息。每个关卡第一行包含两个非负整数n,m,分别表示该关卡中的小猪数量和Kiana输入的神秘指令类型。接下来的n行中,第i行包含两个正实数(xi,yi),表示第i只小猪坐标为(xi,yi)。数据保证同一个关卡中不存在两只坐标完全相同的小猪。
如果m=0,表示Kiana输入了一个没有任何作用的指令。
如果m=1,则这个关卡将会满足:至多用只小鸟即可消灭所有小猪。
如果m=2,则这个关卡将会满足:一定存在一种最优解,其中有一只小鸟消灭了至少只小猪。
保证1<=n<=18,0<=m<=2,0<xi,yi<10,输入中的实数均保留到小数点后两位。
上文中,符号和
分别表示对c向上取整和向下取整
输出格式:
对每个关卡依次输出一行答案。
输出的每一行包含一个正整数,表示相应的关卡中,消灭所有小猪最少需要的小鸟数量
输入输出样例
2 2 0 1.00 3.00 3.00 3.00 5 2 1.00 5.00 2.00 8.00 3.00 9.00 4.00 8.00 5.00 5.00
1 1
3 2 0 1.41 2.00 1.73 3.00 3 0 1.11 1.41 2.34 1.79 2.98 1.49 5 0 2.72 2.72 2.72 3.14 3.14 2.72 3.14 3.14 5.00 5.00
2 2 3
1 10 0 7.16 6.28 2.02 0.38 8.33 7.78 7.68 2.09 7.46 7.86 5.77 7.44 8.24 6.72 4.42 5.11 5.42 7.79 8.15 4.99
6
说明
【样例解释1】
这组数据中一共有两个关卡。
第一个关卡与【问题描述】中的情形相同,2只小猪分别位于(1.00,3.00)和 (3.00,3.00),只需发射一只飞行轨迹为y = -x^2 + 4x的小鸟即可消灭它们。
第二个关卡中有5只小猪,但经过观察我们可以发现它们的坐标都在抛物线 y = -x^2 + 6x上,故Kiana只需要发射一只小鸟即可消灭所有小猪。
【数据范围】
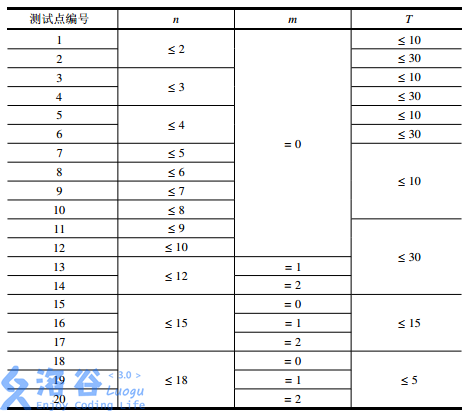
分析:说实话,比较简单的一道状压dp题,可以用一个状态i表示我们该射哪些鸟,dp[i]为在状态i下需要的抛物线的数量,那么可以很容易得到dp[i | 抛物线j射到的猪] = min(dp[i | 抛物线j射到的猪],dp[i] + 1),那么唯一的难点就是求出抛物线j射到哪些猪了,因为只需要2个点就可以确定一条抛物线,先枚举两头猪,确定一条抛物线,将a > 0的去掉,然后在枚举看哪些猪在这条抛物线上就可以了,不过需要注意的三个特殊情况:1.精度问题
2.抛物线可能只能打到一头猪 3.抛物线上两个点横坐标不能相同.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #include <queue> #include <stack> #include <cstdio> #include <iostream> #include <cstring> #include <algorithm> #include <string> using namespace std; int T, n, m,zhuangtai[20][20],dp[1 << 20]; struct node { double x, y; }e[20]; bool jingdu(double a, double b) { return fabs(a - b) < 1e-6; } int main() { scanf("%d", &T); while (T--) { memset(zhuangtai, 0, sizeof(zhuangtai)); scanf("%d%d", &n, &m); for (int i = 1; i <= n; i++) scanf("%lf%lf", &e[i].x, &e[i].y); for (int i = 1; i <= n; i++) for (int j = i + 1; j <= n; j++) if (i != j) { if (jingdu(e[i].x, e[j].x)) continue; double a = (e[j].y / e[j].x - e[i].y / e[i].x) / (e[j].x - e[i].x); double b = e[i].y / e[i].x - a * e[i].x; if (a >= 0.0) continue; for (int k = 1; k <= n; k++) if (jingdu(a * e[k].x * e[k].x + b * e[k].x, e[k].y)) zhuangtai[i][j] |= (1 << (k - 1)); } for (int i = 1; i < (1 << n); i++) dp[i] = 2000000000; dp[0] = 0; for (int i = 0; i < (1 << n); i++) for (int j = 1; j <= n; j++) if (!(i & (1 << (j - 1)))) for (int k = j; k <= n; k++) { if (k == j) dp[i | (1 << (j - 1))] = min(dp[i | (1 << (j - 1))], dp[i] + 1); if (jingdu(e[j].x, e[k].x)) continue; dp[i | zhuangtai[j][k]] = min(dp[i | zhuangtai[j][k]], dp[i] + 1); } printf("%d\n", dp[(1 << n) - 1]); } return 0; }



