洛谷P1886 滑动窗口

P1886 滑动窗口

• • 454通过
  • 1.4K提交
• 题目提供者darkfire
• 标签云端↑
• 难度普及+/提高
• 时空限制1s / 128MB

 提交  讨论  题解  

最新讨论更多讨论

• 滑动窗口
• 求标明空间限制
• 一个奇怪的问题
• 水印233
• 为什么会wa一个点，求dalao…
• 求大神指点

题目描述

现在有一堆数字共N个数字（N<=10^6），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1 3 -1 -3 5 3 6 7], and k = 3.

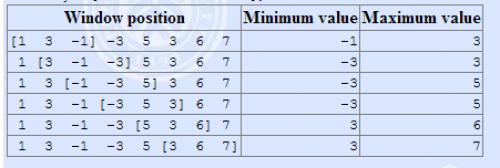
输入输出格式

输入格式：

 

输入一共有两行，第一行为n,k。

第二行为n个数(<INT_MAX).

 

输出格式：

 

输出共两行，第一行为每次窗口滑动的最小值

第二行为每次窗口滑动的最大值

 

输入输出样例

输入样例#1：

8 3
1 3 -1 -3 5 3 6 7

输出样例#1：

-1 -3 -3 -3 3 3
3 3 5 5 6 7

说明

50%的数据，n<=10^5

100%的数据，n<=10^6

分析：这道题可以用线段树做，但是有一种更简单的方法叫做单调队列.我们可以维护一个队列，这个队列是严格递增或者严格递减的，这样当我们需要查询的时候直接输出队首元素即可，那么怎么维护呢？

       假设我们要维护一个严格递增的队列，考虑元素i,如果当前队尾的元素比i大，那么i不能插入到队尾，需要向前移，直到找到一个元素j不大于i,把i置于j后面，那么i之后的元素呢？我们可以全部舍弃掉，因为维护严格递增的队列的目的是求最小值，i之后的元素已经大于i了，这样可以确保队首元素是最小值，如果一个窗口内的元素全部被删光了，那么我们直接加入元素i并且直接输出即可,要注意每次插入i的时候都要检查i的位置与队首的位置差是不是小于等于k,求得的值不能在窗口之外.   对于求最大值，类似.

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<queue>

using namespace std;

int n, k,head,tail,a[1000010],q[1000010],num[1000010];

void getmin()
{
    for (int i = 1; i < k;i++)
    {
        while (head <= tail && i - num[head] >= k)
            head++;
        while (head <= tail && a[i] < q[tail])
            tail--;
        q[++tail] = a[i];
        num[tail] = i;
    }
    for (int i = k; i <= n; i++)
    {
        while (head <= tail && i - num[head] >= k)
            head++;
        while (head <= tail && a[i] < q[tail])
            tail--;
        q[++tail] = a[i];
        num[tail] = i;
        printf("%d ", q[head]);
    }
}

void getmax()
{
    memset(num, 0, sizeof(num));
    memset(q, 0, sizeof(q));
    for (int i = 1; i < k; i++)
    {
        while (head <= tail && i - num[head] >= k)
            head++;
        while (head <= tail && a[i] > q[tail])
            tail--;
        q[++tail] = a[i];
        num[tail] = i;
    }
    for (int i = k; i <= n; i++)
    {
        while (head <= tail && i - num[head] >= k)
            head++;
        while (head <= tail && a[i] > q[tail])
            tail--;
        q[++tail] = a[i];
        num[tail] = i;
        printf("%d ", q[head]);
    }
}

int main()
{
    scanf("%d%d", &n, &k);
    head = 1, tail = 1;
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    head = 1, tail = 1;
    getmin();
    printf("\n");
    head = 1, tail = 1;
    getmax();

    return 0;
}