博客作业06--图
1.学习总结
1.1图的思维导图
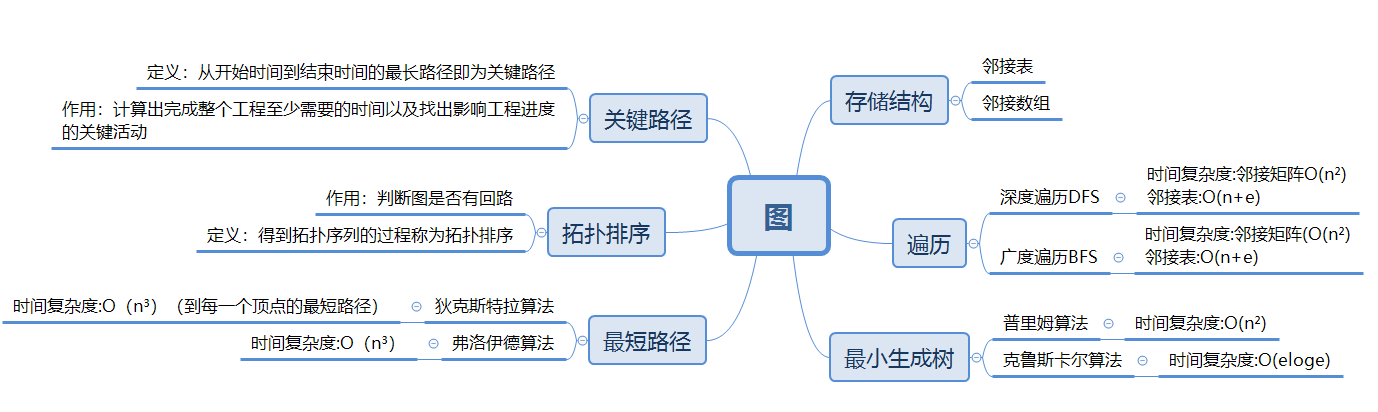
1.2 图结构学习体会Dijkstra
深度遍历DFS通过递归实现,代码简洁,广度遍历BFS通过队列实现,代码略长。都是对图的遍历,两种都行,有不同的作用。
prim算法用来求最小生成树,用lowcost数组存放最小的路可以说是很巧妙地算法,有点长,有点难背,求最短生成树时还能用卡鲁斯卡尔算法。
Dijkstra算法用来求最短路径,通过path数组存放前驱,dist数组存放从初始点到下标点的权值,更加的巧妙,同样求最短路径还可以用弗洛伊德算法。
拓扑排序可以用栈也可以用队列,通过在结构体新加一个变量表示入度来实现。
2.PTA实验作业
2.1 题目1:7-3 六度空间
2.2 设计思路
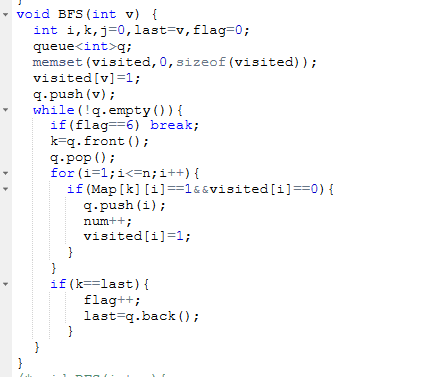
主要函数BFS:
定义一个队列q和判断是否经过的数组visited,可能认识的朋友num
定义一个last表示六层空间中的最后一层初始化为v,层数初始化为0
将初始点v存入队列,并且visited[v]=1
while(队列不为空)
如果层数为6则退出循环
将队列头元素赋给k并出队
for i=0 to n
如果k到i有路径并且没有走过i
将i入队
visit[i]置为1即走过这个点
num++
如果last等于v即走到这一层的最后
last等于队列的最后一个元素
层数加1
2.3 代码截图
2.4 PTA提交列表说明
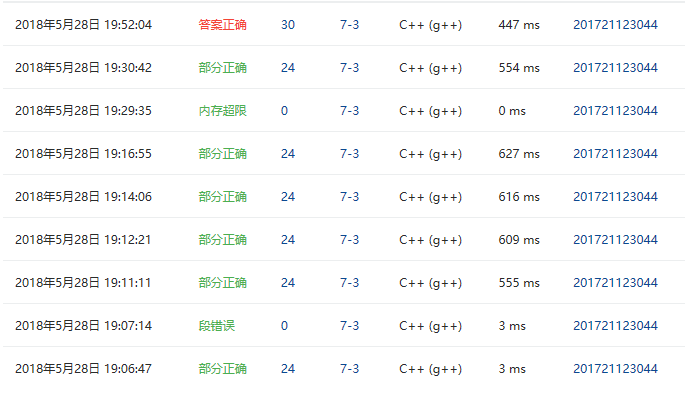
一开始不知道怎么做,没有思路,广度遍历一层后在进行五次深度遍历,仔细阅读题目并思考后发现要六层广度遍历
2.1 题目2:7-4 公路村村通
2.2 设计思路
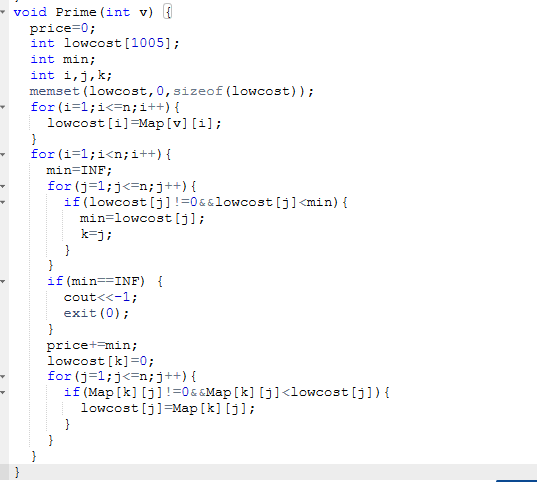
prime函数:
定义一个价格price初始化为0,最低权值数组lowcost
for i=0 to n
lowcost[i]=map[v][i]即初始化为初始节点到每一个节点的权值
for i=1 to n-1
定义min为赋值为INF即32767
for j=1 to n
如果lowcost[j]不为0并且值小于min
更新min即min=lowcost[j]
记录下标k=j
如果min等于INF即没有不重复的路径可走
输出-1,并结束程序
当前路径价格加入总价格price+=min
for j=1 to n
如果k到j有路径并且权值小于lowcost[j]
更新lowcost等于k到j的权值
2.3 代码截图
2.4 PTA提交列表说明
之所以这么惨不忍睹是因为图初始化时我全部初始化为0,前面几题广度深度这样初始化不会有错,可是求最小生成树和最短路径就会出错,当用到最小生成树和最短路径时,应该是行下标和列下标相同时赋值0,不同时赋值INF
2.1 题目3:7-7 旅游规划
2.2 设计思路
Dijkstra函数:
在原有的Dijkstra算法上进行修改
新增一个money数组存储价格作用与dist数组类似,dist数组用来存储距离
money数组初始化为初始点与每个节点的价格,与dist数组类似
在修改最短路径时
如果发现有更短的路径
则对money数组进行修正,即money[j]=money[u]+edges[u][j].price;
如果路径距离相同的话价格较低(重点)
则修正dist数组与money数组
修改前驱即path进行修改
2.3 代码截图

2.4 PTA提交列表说明

一开始只在最短路径相同价格较低里修改money数组没有在有更短路径时修改导致错误
3.截图本周题目集的PTA最后排名
3.1 PTA排名

3.2 我的总分:310
4. 阅读代码
#include <stdio.h>
#include <malloc.h>
#define MaxSize 100
#define M 4
#define N 4
//以下定义邻接表类型
typedef struct ANode //边的结点结构类型
{
int i,j; //该边的终点位置(i,j)
struct ANode *nextarc; //指向下一条边的指针
} ArcNode;
typedef struct Vnode //邻接表头结点的类型
{
ArcNode *firstarc; //指向第一条边
} VNode;
typedef struct
{
VNode adjlist[M+2][N+2]; //邻接表头节点数组
} ALGraph; //图的邻接表类型
typedef struct
{
int i; //当前方块的行号
int j; //当前方块的列号
} Box;
typedef struct
{
Box data[MaxSize];
int length; //路径长度
} PathType; //定义路径类型
int visited[M+2][N+2]= {0};
int count=0;
void CreateList(ALGraph *&G,int mg[][N+2])
//建立迷宫数组对应的邻接表G
{
int i,j,i1,j1,di;
ArcNode *p;
G=(ALGraph *)malloc(sizeof(ALGraph));
for (i=0; i<M+2; i++) //给邻接表中所有头节点的指针域置初值
for (j=0; j<N+2; j++)
G->adjlist[i][j].firstarc=NULL;
for (i=1; i<=M; i++) //检查mg中每个元素
for (j=1; j<=N; j++)
if (mg[i][j]==0)
{
di=0;
while (di<4)
{
switch(di)
{
case 0:
i1=i-1;
j1=j;
break;
case 1:
i1=i;
j1=j+1;
break;
case 2:
i1=i+1;
j1=j;
break;
case 3:
i1=i, j1=j-1;
break;
}
if (mg[i1][j1]==0) //(i1,j1)为可走方块
{
p=(ArcNode *)malloc(sizeof(ArcNode)); //创建一个节点*p
p->i=i1;
p->j=j1;
p->nextarc=G->adjlist[i][j].firstarc; //将*p节点链到链表后
G->adjlist[i][j].firstarc=p;
}
di++;
}
}
}
//输出邻接表G
void DispAdj(ALGraph *G)
{
int i,j;
ArcNode *p;
for (i=0; i<M+2; i++)
for (j=0; j<N+2; j++)
{
printf(" [%d,%d]: ",i,j);
p=G->adjlist[i][j].firstarc;
while (p!=NULL)
{
printf("(%d,%d) ",p->i,p->j);
p=p->nextarc;
}
printf("\n");
}
}
void FindPath(ALGraph *G,int xi,int yi,int xe,int ye,PathType path)
{
ArcNode *p;
visited[xi][yi]=1; //置已访问标记
path.data[path.length].i=xi;
path.data[path.length].j=yi;
path.length++;
if (xi==xe && yi==ye)
{
printf(" 迷宫路径%d: ",++count);
for (int k=0; k<path.length; k++)
printf("(%d,%d) ",path.data[k].i,path.data[k].j);
printf("\n");
}
p=G->adjlist[xi][yi].firstarc; //p指向顶点v的第一条边顶点
while (p!=NULL)
{
if (visited[p->i][p->j]==0) //若(p->i,p->j)方块未访问,递归访问它
FindPath(G,p->i,p->j,xe,ye,path);
p=p->nextarc; //p指向顶点v的下一条边顶点
}
visited[xi][yi]=0;
}
int main()
{
ALGraph *G;
int mg[M+2][N+2]= //迷宫数组
{
{1,1,1,1,1,1},
{1,0,0,0,1,1},
{1,0,1,0,0,1},
{1,0,0,0,1,1},
{1,1,0,0,0,1},
{1,1,1,1,1,1}
};
CreateList(G,mg);
printf("迷宫对应的邻接表:\n");
DispAdj(G); //输出邻接表
PathType path;
path.length=0;
printf("所有的迷宫路径:\n");
FindPath(G,1,1,M,N,path);
return 0;
}

这是迷宫问题,通过图结构邻接表再接深度遍历完成,当初老师第一次说的时候我还不懂,现在再看懂了很多,通过把图中能走的点做成图,就变成了从进入点到迷宫出宫的路径问题,这样一看问题就没有那么复杂,通过DFS的递归,可以很好的面对周围全是墙没有可走点的问题,不过这个DFS不是对图全部可走节点的遍历,就像求树的最大宽度一样用一个数组表示路上的结点,直到当前经历结点是最后的出口就输出,如果没路可走以后就会递归回去就会改这个数组的值。

