博弈论 斯坦福game theory stanford week 4.0_

博弈论 斯坦福game theory stanford week 4-0

perfect information extensive form: taste 完美的信息广泛的形式：品味

包含时间的博弈形式

一般的博弈的形式中并不包括序列的变量，比如时间变量，或者博弈者的动作序列

所以现在我们可以引入拓展形式来描述上述这些问题

这种形式分为两种：

• 完美信息形式
• 不完美信息形式

完美信息博弈

我们这样定义通过一个结构：

• N 代表博弈者的集合
• A 代表行为的集合
• 剩下的部份是选择点和这些点的标签
  • H 代表无终端的选择点
  • x 所有的可能的行为的集合
  • 行为的选择
• Z 终端点，终结点，与无终端点相排斥的点
• 收益函数，

完美信息博弈的例子

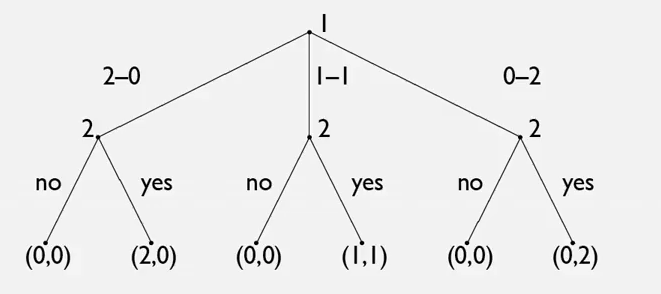
这是一个关于分钱的博弈，两个人分两块钱

第一个博弈者有三个选项，2-0，1-1，0-2这三种分钱的方式。

对于这三个选择，博弈者二都有两个选择。

同意和不同意

例子中的纯策略

这个例子中有多少的纯策略呢？

1 有一个选择点，但是这个点有三个分支。

2 有三个选择点，每个选择点有两个分支。

但是我们的纯策略有八种，这是所以是8.也就是说节点二不是选择一个决策，而是应对1 的每一个决策选择一个决策。

我们定义： 在一个完美信息拓展决策中，一个人的纯策略的个数通过上述公式确定。

一个更加复杂的例子是这样的

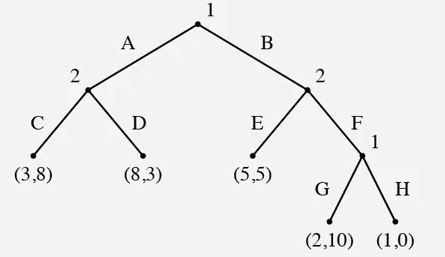
玩家2 的选择有多少种呢？

答案是4种：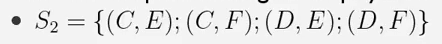

玩家一的呢？

同样是四种，因为即使有的时候他的第二次决策是并没有实际效果的，但是在决策开始前他也必须做出。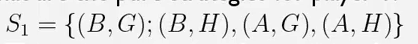

在我们定义了纯策略的定义后，我们就可以轻易的得到下面定义：

混合策略

最优响应

纳什均衡

标准的形式和拓展的形式

对于有些的拓展形式是可以转化成一般形式的，比如例子1.

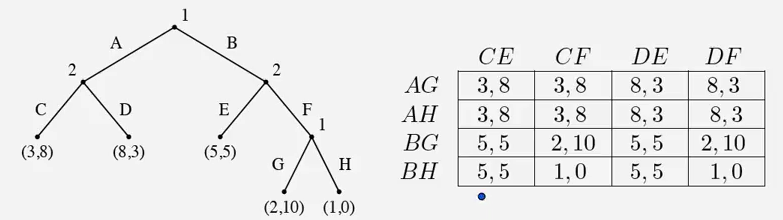
如下图所示。

我们可以发现，这种形式会产生冗余，比如左上角和右上角

定理：每一个完美信息博弈都有一个纳什均衡

那么这个博弈的纯策略纳什均衡是多少呢？

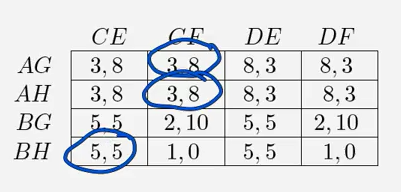
答案是我圈出的那个，具体的方法可以使用前面学到的方法进行求解。

subgame perfection 子博弈完美性

在这个博弈中

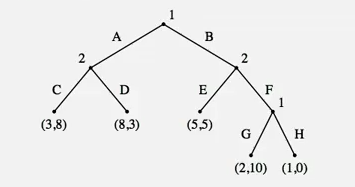
有一个纳什均衡是（BH）（CE）

我们看到如果 1 有机会进行第二次选择，对他来说，他一定不会选择H，而是会选择G

不过他这样做是在威胁2，从而让他选择F

在这样的情境下，我们进行这样的两个定义

在h的根下的子游戏G

这个问题就表明了，有的时候子博弈的纳什均衡有的时候并不是完整博弈的完整性。

下面的那个纳什均衡是子博弈完美的呢？

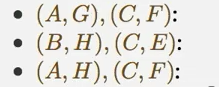
（AG）(CF)是子博弈完美的

因为他的子博弈的纳什均衡和完整博弈的纳什均衡是一致的。

其他的博弈都是不可信的

Backward induction 后向诱导

在这种的情况下，我们怎么计算子博弈的完美均衡呢？

思路就是，先从最低端开始寻找，然后一点点的向上寻找。

对于这个问题，我们可以使用上面的算法来求解。

不过对于零和问题，我们可以将问题进行简化。我们可以很轻易的衡量每一个节点的得失，因为是零和博弈，你的获得就是我的失去。