windows下结构体的数据对齐

前言

比如有些平台每次读都是从偶地址开始，如果一个int型（假设为32位系统）如果存放在偶地址开始的地方，那么一个读周期就可以读出，而如果存放在奇地址开始的地方，就可能会需要2个读周期，并对两次读出的结果的高低字节进行拼凑才能得到该int数据。数据对齐(Data Alignment) 这个要求可以提高存储器系统的性能，减少寻址次数，代价是浪费了一些空间。换句话说是用相对廉价的空间换得时间。

数据对齐

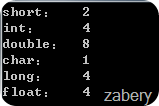
在我计算机上的各基本类型的所占字节数如下：

有结构体A如下：

struct A
{
    int i;
    double d;
    char c;
    short s;
};

数据对齐有两种方式，一种是自然对齐，另一种是强制对齐。

自然对齐

结构体数据自然对齐要满足的条件：

1. 假设数据的偏移量X，数据所属类型所占字节数b，那么需要满足 X % b == 0。

2. 假设结构体中所占总字节数为N，结构体中占字节数最大的数据类型（比如结构体A中的double）的字节数为B。那么需要满足 N % B == 0。

现在分析结构体A

int i; int型占4个字节，结构体的第一个数据，所以偏移量为0（偏移量的单位是字节），能够整除4，满足条件一

double d; double 型占8个字节，偏移量为4，不能够整除8，不满足条件一，所以将其偏移量后移至8，从而满足条件一。

char c; char型占1个字节，偏移量为16，能够整除1，满足条件一。

short s; short型占2个字节，偏移量为17，不能够整除2，不满足条件一，所以将其偏移量后移至18，从而满足条件一。

综上所述: i的偏移量是0，d的偏移量是8，c的偏移量是16，s的偏移量是18。

假设struct A的起始地址为Addr，那么i,d,c,s的内存地址是Addr+各自的偏移量。

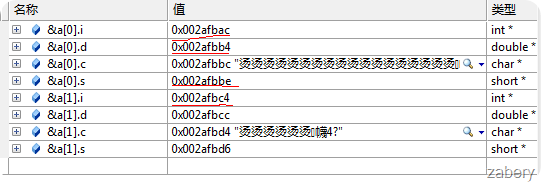
将所有字节加起来应该是20个字节，即struct A所占的内存空间应该是（结构体A的起始地址 ~ 结构体A的起始地址+19）。但是不满足条件2，在struct A中占字节数最大的数据类型是double占8个字节，所以总字节数为24。如何验证这一说呢？可以声明一个结构体数组A a[2]；如果struct A真的占字节数为24，那么&a[1].i – &a[0].i的值应该等于24。换言之，short s占了两个字节之后还另占了4个字节的内存地址保持数据的对齐，&a[1].i – &a[0].i = 6。有图有真相：

从图中观察到两点

1.每个数据的内存地址都是struct A的起始地址（0x002afbac）+各自的偏移量。

2.&a[1].i  - &a[0].s = 6从而验证了上面加粗字的内容为真。

强制对齐

强制对齐需要用到#pragma pack

#pragma pack(1)

    struct B
    {
        int i;
        double d;
        char c;
        short s;
    };
#pragma pack()

先不理会#pragma pack的具体功能，只需要知道它有一个参数即可。

结构体的强制对齐要满足：

1. 假设数据的偏移量X，数据所属类型所占字节数b1，#pragma pack(b2)的参数为b2，那么需满足 X % ( min ( b1, b2) ) == 0。

2. 假设结构体中所占总字节数为N，结构体中占字节数最大的数据类型（比如结构体A中的double）的字节数为B1，#pragma pack(b2)的参数为B2，那么应该满足

N % ( min( B1, B2) ) == 0。

#pragma pack( n ) 的作用就在条件1，2中体现了，也体现了强制对齐与自然对齐的区别。

现在分析结构体B（与结构体唯一的区别就是加了pack）所占的总字节数：

int i；偏移量为0，能够整除min (4, 1)。

double d；偏移量为4，能够整除min (8, 1)

char c；偏移量为12，能够整除min (1, 1)

short s；偏移量为13，能够整除min (2, 1)

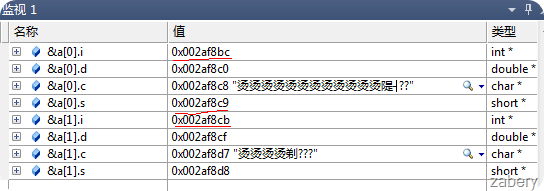
所以最后的总字节数为15。又15能够整除min (8, 1)，满足条件2，因此最后的总字节数为15。见真相：

总结

自然对齐其实是有默认的pack，在我的计算机中它的默认值为8（可通过#pragma pack(show)来查询默认值，运行的时候在警告栏中显示），也就是本文中的自然对齐与

#pragma pack(8)

    struct A
    {
        int i;
        double d;
        char c;
        short s;
    };
#pragma pack()

是等价的。