hdu 2586 欧拉序+rmq 求lca

题意:求树上任意两点的距离

先说下欧拉序

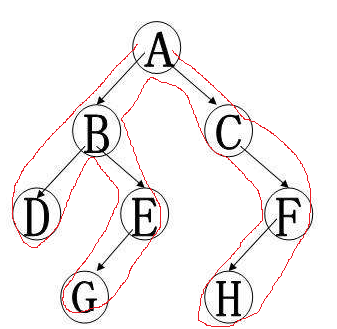
对这颗树来说 欧拉序为 ABDBEGBACFHFCA 那欧拉序有啥用

这里先说第一个作用 求lca

对于一个欧拉序列，我们要求的两个点在欧拉序中的第一个位置之间肯定包含他们的lca,因为欧拉序1上任意两点之间肯定包含从第一个点走到第二个点访问的路径上的所有点

所以只需要记录他们的深度，然后从两个询问子节点x,y第一次出现的位置之间的深度最小值即可,可能不大好理解,看张图吧。

 

也就是说求lca可以转换为求一段区间的最值问题，结合rmq就可以处理啦

对于2586这题有个结论：树上任意两个点的距离等于两个点到根的距离之和减去2倍lca到根的距离

上代码

：

#include <cstdio>
#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
struct node
{
    int x;
    ll cost;
};
vector<node> edge[40010];
ll dis[40010];// 到根节点的距离
int dep[80010];
int ver[80010];// 欧拉序列
int first[40010];// 在欧拉序中第一次出现的位置
int vret;//
int n,m;
int mn[80010][20];
void dfs(int x,int fa,int deep) // 求出欧拉序 以及每个点对应的度
{
    ver[++vret]=x;
    first[x]=vret;
    dep[vret]=deep;
    int len=edge[x].size();
    for(int i=0;i<len;i++)
    {
        node temp=edge[x][i];
        if(temp.x!=fa)
        {
            dis[temp.x]=dis[x]+temp.cost;
            dfs(temp.x,x,deep+1);
            ver[++vret]=x;
            dep[vret]=deep; //
        }
    }
}
void st(int n)// 维护的是欧拉序 长度需要注意一下
{
    int temp=(int)floor(log2(double(n)));
    for(int i=1;i<=n;i++) mn[i][0]=i;// 注意一下 这里维护的是点 不是单纯的值
    for(int j=1;j<=temp;j++)
    {
        for(int  i=1;i+(1<<j)-1<=n;i++)
        {
            int a=mn[i][j-1];
            int b=mn[i+(1<<(j-1))][j-1];
            if(dep[a] < dep[b]) mn[i][j]=a;
            else mn[i][j]=b;
        }
    }
}
int rmq(int x,int y)
{
    int k=(int)(log(double(y-x+1))/log(2.0));
    int a=mn[x][k];
    int b=mn[y-(1<<k)+1][k];
    if(dep[a] < dep [b]) return a;
    else return b;
}
int lca(int x,int y)
{
    int fx=first[x];
    int fy=first[y];
    if(fx>fy) swap(fx,fy);
    return  rmq(fx,fy);
}
void init()
{
    vret=0;
    dis[1]=0;
    for(int i=1;i<=n;i++) edge[i].clear();
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        init();// edge
        scanf("%d %d",&n,&m);
        for(int i=1;i<n;i++)
        {
            int x,y;
            ll cost;
            scanf("%d %d %lld",&x,&y,&cost);
            node temp;
            temp.cost=cost;
            temp.x=x;
            edge[y].push_back(temp);
            temp.x=y;
            edge[x].push_back(temp);
        }


        dfs(1,1,1);//
        st(2*n-1);

        for(int i=1;i<=m;i++)
        {
            int x,y;
            cin>>x>>y;
            int temp=lca(x,y);// point
            cout<<dis[x]+dis[y]-2*dis[temp]<<endl;
        }
    }
    return 0;
}