数据结构_图总结

图

注：图可以看成是一种特殊的“树”，特殊在一个节点可有多个父节点（因此也就可能出现环），故其遍历算法与树几乎一致，只不过需要借助visited[]来剪枝——标记访问过的节点以免重复访问。图的很多算法均以遍历算法为基础。

定义

G=(V,E)

顶点偶对：（通常不考虑自环，即认为vi, vj不同）

(vi, vj)，无向边、无向图，vi, vj 互为邻接点

<vi, vj>，有向边（亦称为弧）、有向图，vi 为 vj 的邻接点，vi为弧尾、vj为弧头

带权的图称为网络。

基本术语

1、度（TD）、入度（ID）、出度（OD）：各节点度的和等于边数的2倍：2e=(i=1~n)Σ TD(vi)，有向图、无向图均如此。有向图入度和、出度和、边数 三者相等。

=>  无向图度和最大为n(n-1)，故边数最多n(n-1)/2，此时为完全图。

有向图度和最大为2n(n-1)，故边数最多n(n-1)，此时为有向完全图。

=>  稠密图、稀疏图（边或弧的数目是否接近完全图）

2、路径：若顶点序列v1v2...vm有(vi,vi+1)∈E(i=1,2,...m-1)，则为v1到vm的一条路径，有向图类似。

回路或环：起点、终点重合的路径。判断是否有回路可用下面介绍的深度优先遍历或拓扑排序。

简单路径：序列中顶点不重复的路径

简单回路或简单环：除首末顶点外其他顶点均不重复的回路

有根图：有向图若存在一个顶点有到其他所有顶点的路径，则为有根图，此顶点为根

3、子图：G,=(V,, E,)，其中  G, ⊆ G、V, ⊆ V,  E, ⊆ E

4、连通：

顶点连通：无向图顶点vi到vj（i≠j）有路径，则vi vj连通；有向图则要求vi到vj及vj到vi（i≠j）都有路径才是连通

连通图：无向图任意两个顶点间都是连通的则是连通图。对于一有n个顶点的无向图：若是连通图则边数：[n-1, n(n-1)/2]；若要保证是连通图则边至少需是 ：(n-1)(n-2)/2+1，即此时n-1个顶点构成完全图然后再加一条边。

强连通图：有向图任意两顶点间都是连通的则是强连通图。对于一有n个顶点的有向图，若是强连通图则边数：[n, n(n-1)]；若要保证是连通图则边至少需是：(n-1)(n-2)+2。

连通分量：无向图的极大连通子图。

强连通分量：有向图的极大连通子图。

连通图的连通分量只有一个即为本身，而非连通图的连通分量有多个；强连通图亦然。

5、生成树：连通图包含n个顶点的极小连通子图为其生成树。

连通图才有生成树，其包含n个顶点、n-1条边；生成树可能不唯一，且不一定是最小生成树。

上一篇文章中介绍的“树”其实就是一种特殊的图——连通无环的图。

图的存储

无向图：邻接矩阵、邻接表、多重邻接表法

有向图：邻接矩阵、邻接表、十字链表法

1、邻接矩阵存储（存所有边，若不带权则不存在的边包括自己到自己表示为0、若带权则表示为∞）

无向图的邻接矩阵是个对称阵，可以用矩阵的压缩存储。

2、邻接表存储（存顶点和和该节点邻接的边，与邻接矩阵存储相比不用存不存在的边）：

法1：顺序存储与链式存储相结合。（顶点节点、边节点）

无向图邻接表中顶点节点、边节点数分别为n、2e，有向图的则分别为n、e。故无向图邻接表边节点数为偶数，若边节点数为奇数则为有向图。

顶点节点、边节点定义：

 1 typedef struct edge//边节点 
 2 {
 3     int adjvex;//该边的终止节点在顶点节点数组中的位置 
 4     int weight;//边的权重，带权图才需要。 
 5     struct edge* next;//指向下一边节点 
 6 }ELink;
 7 
 8 typedef struct ver//顶点节点 
 9 {
10     int vertex;//顶点节点的信息
11     ELink * link;//指向第一个边节点 
12 }VLink;
View Code

法2：都用顺序存储：存储每个节点的【邻接节点（无向图）】或【下一个节点（有向图）】，示例：

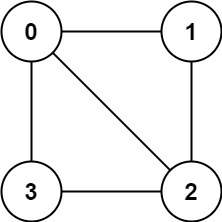
 graph = [[1,2,3],[0,2],[0,1,3],[0,2]] 

这种更简洁，本质上与邻接矩阵类似只不过去掉了不存在的边的存储。

 

有向图 第i行非0元素的个数（邻接矩阵存储）或第i个链表边节点的个数（邻接表存储） 等于该节点的出度OD，所有行非0元素个数和或所有链表边节点个数和等于边数e。

无向图 第i行非0元素的个数（邻接矩阵存储）或第i个链表边节点的个数（邻接表存储） 等于该节点的度TD，所有行非0元素个数和或所有链表边节点个数和等于两倍边数2e。

 

在实际题目中，两种存储方式中邻接表更常用，很多问题中输入数据是边集合，此时解决问题的第一步就是把输入数据转成邻接表、然后基于邻接表进行遍历从而解决问题。

 

图的遍历

指访问每个顶点一次且仅一次。

遍历的过程实质上是通过边或弧寻找邻接点的过程，因此遍历过程中也会访问每一条边。而采用不同遍历方法时总边节点数是不变的，所以深度优先、广度优先的时间复杂度一样。针对不同存储方法（邻接矩阵、邻接表）的遍历算法类似。

  邻接矩阵存储 邻接表存储
深度优先（递归） O(n2) O(n+e)
广度优先（非递归，借助优先队列） O(n2) O(n+e)

图论相关算法可看成是二叉树算法的一种延续，实际上，图也可看成是个特殊的多叉“树”——特殊在【两个节点可能有共同的子节点、进一步地可能有环（即子节点也可能是父节点的父节点）】，因此图的遍历与多叉树的遍历非常类似。当图中不存在环时，图就是一棵树了。

图的遍历框架总结可参阅labuladong图论基础总结。

图的DFS遍历 -> 多叉树树的DFS遍历 -> 二叉树的DFS遍历 -> 单链表的DFS遍历 本质上是类似的，可参阅labuladong数据结构和算法框架思维-数据结构的基本操作；其BFS也是类似的，类比和算法框架见labuladong BFS算法框架。

强烈建议阅读这几篇文章，异常简洁、提纲掣领！！ 

邻接表存储的图的DFS遍历框架伪代码：

    // 记录被遍历过的节点
    boolean[] visited;
    // 记录从起点到当前节点的路径
    boolean[] onPath;
    /* 图遍历框架 */
    void traverse(Graph graph, int s) {
        if (visited[s])
            return;
        // 经过节点 s，标记为已遍历
        visited[s] = true;
        // 做选择：标记节点 s 在路径上
        onPath[s] = true;

        // 若要前序遍历，则在此对当前节点处理
        // do something to s

        // dfs递归
        for (int neighbor : graph.neighbors(s)) {
            traverse(graph, neighbor);
        }
        // 若要后续遍历，则在此对当前节点进行处理
        // do something to s

        // 撤销选择：节点 s 离开路径
        onPath[s] = false;
    }
邻接表存储的图的DFS遍历框架（前序或后序）

基于该框架的应用和改造可参阅后文环检测与拓扑排序一节。

邻接表存储的图的BFS遍历框架伪代码：

见二叉树、多叉树、图的BFS算法框架伪代码-MarchOn。

注：

由于环的存在，遍历时的一个特点是需要借助 visited[] 来辅助记录遍历过的节点以免重复遍历导致结束不了，相当于回溯算法中的剪枝功能。在实际问题中不一定要有专门的visited[]，有时可省略转而借助输入数据来达到相同效果（例如岛屿问题中将1变为0来表示访问过），但原理上是相同的。

上述DFS框架中遍历时是把visited判断放在base case进行，下面的DFS实现中是在递归前对相邻节点判断，两种均可、略有差异，但前者更符合递归的写法、与树的递归遍历类似。

1、邻接表存储：O(n+e)

深度优先：

 1 #include<stdio.h>
 2 #include<malloc.h>
 3 typedef struct edge//边节点 
 4 {
 5     int adjvex;//该边的终止节点在顶点节点数组中的位置 
 6     int weight;//边的权重，带权图才需要。 
 7     struct edge* next;//指向下一边节点 
 8 }ELink;
 9 
10 typedef struct ver//顶点节点 
11 {
12     int vertex;//顶点节点的信息
13     ELink * link;//指向第一个边节点 
14 }VLink;
15 
16 
17 void DFS(VLink G[],int n,int visit[],int i)//从下标为i的节点开始遍历，时间复杂度为 O(当前所在连通分量边数) 
18 {
19     //VISIT(i);
20     visit[i]=1;
21     
22     ELink *p=G[i].link; 
23     while(p!=NULL)
24     {
25         i=p->adjvex;
26         if(visit[i]==0)
27         {
28             DFS(G,n,visit,i);
29         }
30         p=p->next;
31     }
32 } 
33 void traverse_DFS(VLink G[],int n,int visit[])
34 {
35     int i;
36     for(i=0;i<n;i++)//O(n)
37     {
38         visit[i]=0;
39     }
40     for(i=0;i<n;i++)//O(n+图的边节点数) = O(n+e) （无向图边节点数为2e、有向图为e，故量级为e） 
41     {
42         if(visit[i]==0)
43         {
44             DFS(G,n,visit,i);//每执行完一次得到一个连通分量
45         }
46     }
47 }
DFS、traverse_DFS

广度优先：

#define M 100
void BFS(VLink G[],int n,int visit[],int i)//从下标为i的节点开始遍历，时间复杂度为 O(当前所在连通分量边数)
{
    int queue[M],front=-1,rear=-1;

    //访问后再入队。若出队再访问则会有问题：若当前节点的一个邻接点已经在队里那此时还要不要重复入队，如何判断？
    //VISIT(i);
    visit[i]=1;
    queue[++rear]=i;//ADDQ

    ELink *p;
    while(front<rear)
    {
        i=queue[++front];

        p=G[i].link;
        while(p!=NULL)
        {
            i=p->adjvex;
            if(visit[i]==0)
            {
                //访问后再入队
                //VISIT(i);
                visit[i]=1;
                queue[++rear]=i;//ADDQ
            }
            p=p->next;
        }
    }
}

//另一种写法，与上法相比 VISIT(i) 位置变了且只用写一处，因此更简洁，推荐此写法
void BFS(VLink G[],int n,int visit[],int i)
{
    int queue[M],front=-1,rear=-1;
    visit[i]=1;
    queue[++rear]=i;

    ELink *p;
    while(front<rear)
    {
        i=queue[++front];
        //VISIT(i);

        p=G[i].link;
        while(p!=NULL)
        {
            i=p->adjvex;
            if(visit[i]==0)
            {
                visit[i]=1;
                queue[++rear]=i;//ADDQ
            }
            p=p->next;
        }
    }
}
View Code

2、邻接矩阵存储：O(n2)，实现与上类似。

以下为Java实现的针对顺序存储的邻接表的DFS、BFS遍历，很简洁。邻接矩阵的与此只有细微差别。

    /** 根据给的的图的邻接矩阵或邻接表进行DFS或BFS遍历 */
    public void traverseGraph(int[][] graph) {
        int n = graph.length;
        boolean[] visited = new boolean[n];// 初始为false
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                bfs(graph, i, visited);
            }
        }
    }

    /** 根据给定的图的邻接表和起始节点进行BFS遍历 */
    public void bfs(int[][] graph, int i, boolean[] visited) {
        Queue<Integer> queue = new LinkedList<>();// 队列里的节点都是访问过的节点

        // VISIT(i)
        visited[i] = true;
        queue.offer(i);

        while (!queue.isEmpty()) {
            i = queue.poll();
            for (int k = 0; k < graph[i].length; k++) {
                int j = graph[i][k];
//                {// 若graph是邻接矩阵，则进行此处理以确保i,j间是一条边
//                    if (j != 0 && j != INFINITE) {
//                        j = k;
//                    } else {
//                        continue;
//                    }
//                }
                if (!visited[j]) {
                    // VISIT(j)
                    visited[j] = true;
                    queue.offer(j);
                }
            }
        }
    }

    /** 根据给定的图的邻接表和起始节点进行DFS遍历 */
    public void dfs(int[][] graph, int i, boolean[] visited) {

        // VISIT(i)
        visited[i] = true;

        for (int k = 0; k < graph[i].length; k++) {
            int j = graph[i][k];
//            {// 若graph是邻接矩阵，则进行此处理以确保i,j间是一条边
//            if (j != 0 && j != INFINITE) {
//                j = k;
//            } else {
//                continue;
//            }
//        }
            if (!visited[j]) {
                // 注意与BFS的区别，这里不再进行VISIT
                dfs(graph, j, visited);
            }
        }
    }
图的邻接矩阵或邻接表的DFS、BFS

很多问题可抽象为图的遍历问题，实际例子：二分图的判断和划分（详见后面二分图部分）、岛屿问题专题等。

二维矩阵的区域遍历问题与图的遍历问题本质上类似，前者专门的叫法为“FloodFill算法”，岛屿问题就是该算法的应用对象。

 

DFS/BFS：单次调用可得到一个连通分量/强连通分量（访问的点+关联的所有边），时间复杂度为O(连通/强连通分量的边数)。

DFS：亦可得到该分量的一棵生成树（依次访问的点连成的边）；可通过DFS来实现有向图的环检测和拓扑排序，详见后文。

  

以下为网络（即带权图）相关。

最小生成树（MST）

带权图（网络）的生成树中权值和最小的生成树，也叫最小代价生成树。既然是生成树那么就是一个包含n个顶点的连通图，所以能够到达各个顶点，即任意两个顶点间都有路径。最小生成树一般不唯一，但当权值各不相同时唯一。

最小生成树算法（求最大生成树也可以用这两法，只不过每次取权值大的）

1、Prime算法：主要思想是每次从未选点集中找出到已选点集距离最小的边，并把该边的的未选点加入到已选点集即可；初始时未选点集是空集、已选点集是所有点。

时间复杂度为O(n2)。适合顶点少者。

由邻接矩阵求最小生成树。代码如下（与dijkstra的非常相似，只是最后一步的更新信息时不同。可对比参阅）：

 1 int primMST(int n,int dist[][DIM],int s,int pre[])//res为MST的权值，pre为每次选进来一个点时与之对应的已选点 
 2 {
 3     int f[n],mdist[n];//标记是否选取点
 4     
 5     int i;
 6     for(i=0;i<n;i++)//初始化 
 7     {
 8         f[i]=0;
 9         mdist[i]=dist[s][i];
10         pre[i]=s;
11     }
12     f[s]=1;//起点选上 
13     
14     int tmpMinDist;//inf
15     int tmpMinNode;
16     int j;
17     int res=0;
18     for(i=1;i<n;i++)//添加n-1次节点
19     {
20         tmpMinDist=INF_DIST;
21         for(j=0;j<n;j++)//找出未选节点中mdist最小者 
22         {
23             if(!f[j] &&(mdist[j]<tmpMinDist))
24             {
25                 tmpMinDist=mdist[j];
26                 tmpMinNode=j;
27             }
28         }
29         
30         f[tmpMinNode]=1;//将最小者选上并更新到各未选点的距离 
31         res+=dist[tmpMinNode][pre[tmpMinNode]];
32         printf("%2d--%2d\n",pre[tmpMinNode],tmpMinNode);//选择的节点对应的边 
33         for(j=0;j<n;j++)
34         {
35             if( !f[j] && dist[tmpMinNode][j]<mdist[j] )
36             {
37                 mdist[j]=dist[tmpMinNode][j];
38                 pre[j]=tmpMinNode;
39             }
40         }
41     }
42     return res;
43 }
以邻接矩阵存储的图的最小生成树的Prime算法

2、Kruskal算法：主要思想是先对边从小到大排序，然后按序依次尝试将边加入到已选边集，若加入后构成环则不加入否则加入；初始时已选边集为空集。

时间复杂度为O(elge)，边排序。适合边少者。当e=Ω(n2)时Prime比Kruskal好；当e=o(n2)时相反。

最短路径

单源最短路径：O(n2)，求得的源点到各节点的最短路径构成了生成树，但一般不是最小生成树。

1、Dijkstra算法：不含负权的单源最短路径。代码：

 1 #define DIM 6
 2 
 3 //自身到自身的 距离为0 
 4 # define INF_DIST 0x0fffffff
 5 void dijkstra(int n,int dist[][DIM],int s,int mdist[],int pre[])//参数分别表示 节点数、边权值、起点、要到各点的最短距离、最短距离时该点的前一个点 
 6 {
 7     int f[n];//标记是否选取点
 8     
 9     int i;
10     for(i=0;i<n;i++)//初始化 
11     {
12         f[i]=0;
13         mdist[i]=dist[s][i];
14         pre[i]=s;
15     }
16     f[s]=1;//起点选上 
17     
18     int tmpMinDist;//inf
19     int tmpMinNode;
20     int j;
21     for(i=1;i<n;i++)//添加n-1次节点
22     {
23         tmpMinDist=INF_DIST;
24         for(j=0;j<n;j++)//找出未选节点中mdist最小者 
25         {
26             if(!f[j] &&(mdist[j]<tmpMinDist))
27             {
28                 tmpMinDist=mdist[j];
29                 tmpMinNode=j;
30             }
31         }
32         
33         f[tmpMinNode]=1;//将最小者选上并更新到各未选点的距离 
34         for(j=0;j<n;j++)
35         {
36             if( !f[j] && dist[tmpMinNode][j]<INF_DIST &&( mdist[tmpMinNode]+dist[tmpMinNode][j] < mdist[j] ) )
37             {
38                 mdist[j]=mdist[tmpMinNode]+dist[tmpMinNode][j];
39                 pre[j]=tmpMinNode;
40             }
41         }
42     }
43 }
44 void printMinPathForNode(int pre[],int n,int s,int e)//打印从s到e的最短路 
45 {
46     if(s!=e)
47     {
48         printMinPathForNode(pre,n,s,pre[e]);
49     }
50     printf("%d ",e+1);
51 }
以邻接矩阵存储的图的Dijkstra算法

可以看出该算法就是图的BFS 算法的加强版，实际上，与图的BFS遍历一样，它们都是从二叉树的层序遍历衍生出来的。

2、Belman-Ford算法：允许含负权的单源最短路径。比如汇率套汇场景中就是要找到一个权重乘积大于1的环，权重用对数替代时则等价于找新权重和大于0的环，此时就可用此算法。

3、Floyd算法：允许含负权的任意两点的最短路径。

上述几种算法都属于贪心算法。

 

AOV网络（环检测、拓扑排序）、AOE网络（最长路径）

AOV（Activity On Vertex）、AOE（Activity On Edge）网络都是有向图。

1、AOV网络用节点表示活动，一些活动间有先后关系，所以组成了有向图。

判断活动能否顺利开展（即有向图是否有环）：拓扑排序、深度优先遍历，时间复杂度均为O(n+e)。相关框架总结详见labuladong-拓扑排序详解及运用。

法1：DFS。基于邻接表存储的有向图的环检测的DFS算法框架（其他存储方式的图可转为邻接表存储的图），基于前面“遍历”一节的DFS框架稍微修改即可。伪代码：

只检测是否有环：借助onPath[]记录当前遍历路径上哪些节点被访问，路径上的节点重复访问时说明有环。

    // 树/图的递归解法有基于递归迭代（思路对应回溯算法）和基于问题分解（思路对应动态规划或分治算法）两种方式，详见https://www.cnblogs.com/z-sm/p/6796004.html#:~:text=labuldong%E5%88%B7%E9%A2%98%E6%80%BB%E7%BB%93%2D%E4%BA%8C%E5%8F%89%E6%A0%91%E7%B3%BB%E5%88%97%E7%AE%97%E6%B3%95。
    // 这里为前者。
    class CycleDetection {
        // 记录一次递归堆栈中的节点
        boolean[] onPath;
        // 记录遍历过的节点，防止走回头路
        boolean[] visited;
        // 记录图中是否有环
        boolean hasCycle = false;

        boolean hasCycle(List<Integer>[] graph) {
            int n = graph.length;

            visited = new boolean[n];
            onPath = new boolean[n];
            for (int i = 0; i < n; i++) {
                // 遍历图中的所有节点
                traverse(graph, i);
            }
            // 只要没有循环依赖可以完成所有课程
            return hasCycle;
        }

        void traverse(List<Integer>[] graph, int s) {

            if (visited[s]) {
                if (onPath[s]) {
                    // 出现环
                    hasCycle = true;
                }
                return;
            }
            // 前序代码位置
            visited[s] = true;
            onPath[s] = true;
            for (int t : graph[s]) {
                traverse(graph, t);
            }
            // 后序代码位置
            onPath[s] = false;
        }
    }
邻接表存储的有向图的环检测DFS算法框架，只知道有无环 

有环则返回环：借助栈onPath记录当前遍历路径上的节点，路径上节点重复访问时栈中重复节点到栈顶的各节点组成的路径即为环。与上法相比更通用，推荐。

// 树/图的递归解法有基于递归迭代（思路对应回溯算法）和基于问题分解（思路对应动态规划或分治算法）两种方式，详见https://www.cnblogs.com/z-sm/p/6796004.html#:~:text=labuldong%E5%88%B7%E9%A2%98%E6%80%BB%E7%BB%93%2D%E4%BA%8C%E5%8F%89%E6%A0%91%E7%B3%BB%E5%88%97%E7%AE%97%E6%B3%95。
    // 这里为前者。
    class CycleDetection {
        // 记录遍历过的节点，防止走回头路。相当于回溯算法中的剪枝功能
        boolean[] visited;
        // 记录一次递归过程中栈中的节点，相当于回溯算法中的回溯功能
        Stack<Integer> onPath;
        // 上述递归过程中产生环时元素在栈中的位置
        int cycleIndex = -1;

        boolean hasCycle(List<Integer>[] graph) {
            int n = graph.length;

            visited = new boolean[n];
            onPath = new Stack<>();
            for (int i = 0; i < n; i++) {
                // 遍历图中的所有节点
                traverse(graph, i);
            }
            // 得到环
            // onPath[cycleIndex, top]各节点连成的路径即为环
//            while (onPath.size() > cycleIndex) {
//                onPath.pop();
//            }
            return cycleIndex != -1;
        }

        void traverse(List<Integer>[] graph, int s) {
            if (visited[s]) {
                if (onPath.contains(s)) {
                    // 出现环
                    cycleIndex = onPath.indexOf(s);
                }
                return;
            }

            // 前序代码位置
            visited[s] = true;
            onPath.push(s);
            for (int t : graph[s]) {
                traverse(graph, t);
            }
            // 后序代码位置
            onPath.pop();
        }
    }
邻接表存储的有向图的环检测DFS算法框架，有环则返回环

拓扑排序：后续遍历得到的节点列表的反转即为所求（注意前序遍历结果并非所求）。基于上述两法稍加改造即可，这里以基于后者的改造为例：

    // 树/图的递归解法有基于递归迭代（思路对应回溯算法）和基于问题分解（思路对应动态规划或分治算法）两种方式，详见https://www.cnblogs.com/z-sm/p/6796004.html#:~:text=labuldong%E5%88%B7%E9%A2%98%E6%80%BB%E7%BB%93%2D%E4%BA%8C%E5%8F%89%E6%A0%91%E7%B3%BB%E5%88%97%E7%AE%97%E6%B3%95。
    // 这里为前者。
    class CycleDetection {
        // 记录遍历过的节点，防止走回头路。相当于回溯算法中的剪枝功能
        boolean[] visited;
        // 记录一次递归过程中栈中的节点，相当于回溯算法中的回溯功能
        Stack<Integer> onPath;
        // 上述递归过程中产生环时元素在栈中的位置
        int cycleIndex = -1;
        // 后续遍历的结果
        List<Integer> postorder;

        int[] topologyOrder(List<Integer>[] graph) {
            int n = graph.length;

            visited = new boolean[n];
            onPath = new Stack<>();
            postorder = new ArrayList<>();
            for (int i = 0; i < n; i++) {
                // 遍历图中的所有节点
                traverse(graph, i);
            }
            // 得到环
            if (cycleIndex != -1) {
                return new int[0];
            } else {
                int[] res = new int[n];
                for (int i = 0; i < n; i++) {
                    res[i] = postorder.get(n - 1 - i);
                }
                return res;
            }
        }

        void traverse(List<Integer>[] graph, int s) {
            if (visited[s]) {
                if (onPath.contains(s)) {
                    // 出现环
                    cycleIndex = onPath.indexOf(s);
                }
                return;
            }

            // 前序代码位置

            visited[s] = true;
            onPath.push(s);
            for (int t : graph[s]) {
                traverse(graph, t);
            }
            // 后序代码位置
            postorder.add(s);

            onPath.pop();
        }
    }
邻接表存储的有向图的拓扑排序DFS算法框架

法2：BFS。记录各节点的入度，然后依次将入度为0的节点及从其出发的边移除并更新子节点的入度，重复该过程，若能将所有节点移除则说明无环，依次移除的节点列表构成了拓扑排序。

    // BFS拓扑排序
    // 图的遍历 都需要 visited 数组防止走回头路，这里的 BFS 算法其实是通过 indegree 数组实现的 visited 数组的作用，只有入度为
    // 0 的节点才能入队，从而保证不会出现死循环。
    class TopologyOrder {

        int[] topologyOrder(List<Integer>[] graph) {
            // 1 记录每个节点的入度
            int[] indegree = new int[graph.length];
            for (List<Integer> nexts : graph) {
                for (int next : nexts) {
                    indegree[next]++;
                }
            }
            // 2 类似图的BFS的过程
            Queue<Integer> queue = new LinkedList<>();// 存放排序过程中度为0的节点
            for (int i = 0; i < graph.length; i++) {
                if (indegree[i] == 0) {
                    queue.offer(i);
                }
            }
            int[] res = new int[graph.length];
            int resIndex = 0;
            while (!queue.isEmpty()) {
                int q = queue.poll();
                res[resIndex++] = q;
                for (int next : graph[q]) {
                    indegree[next]--;
                    if (indegree[next] == 0) {
                        queue.offer(next);
                    }
                }
            }
            // 3 结果
            for (int i = 0; i < graph.length; i++) {
                if (indegree[i] != 0) {// 说明有环
                    res = null;
                    break;
                }
            }
            return res;
        }
    }
邻接表存储的有向图的拓扑排序BFS算法框架

2、AOE网络：是个有向无环图（DAG），且入度为零的点、出度为零的点分别有且仅有一个。

在AOE网络中，顶点表示事件、边表示活动、边上的权值表示该活动的时间代价。某顶点表示的事件发生后从该顶点出发的各有向边表示的活动才能发生、进入某顶点的各有向边表示的活动发生后该顶点表示的事件才能发生。AOE网络通常用来安排工程的工序。

事件最早发生时间：从前往后，多入取大者（因为不能早于入活动的结束时间，源节点此值为0。

事件最晚发生时间：从后往前，多出取小者（因为不能晚于出活动的开始时间），终节点此值取上步得到的值。

活动最早发生时间：从前往后，前驱事件的最早发生时间

活动最晚发生时间：从后往前，后继事件的最晚发生时间减当前活动的时间

松弛时间：活动最早发生时间与最晚发生时间的差值

关键路径：松弛时间为0的活动构成的路径，其权值和为网络的最大路径长度（Dijkstra等则可以求最短路径，注意区别），亦为工程的最短完成时间。路径可能不唯一，但权值和一样。

 

其他图论相关算法

并查集算法

用于解决图的动态连通判断问题，具体可参阅：https://www.cnblogs.com/z-sm/p/12383918.html

 

 

二分图

二分图：若无向图 G=(V,E) 的顶点集 V 可以分割为两个互不相交的子集，且图中每条边的两个顶点分别属于这两子集，则称图 G 为一个二分图。二分图 <=> 两种颜色给所有节点染色后【每个节点的颜色都与其相邻节点的都颜色不同】的图。

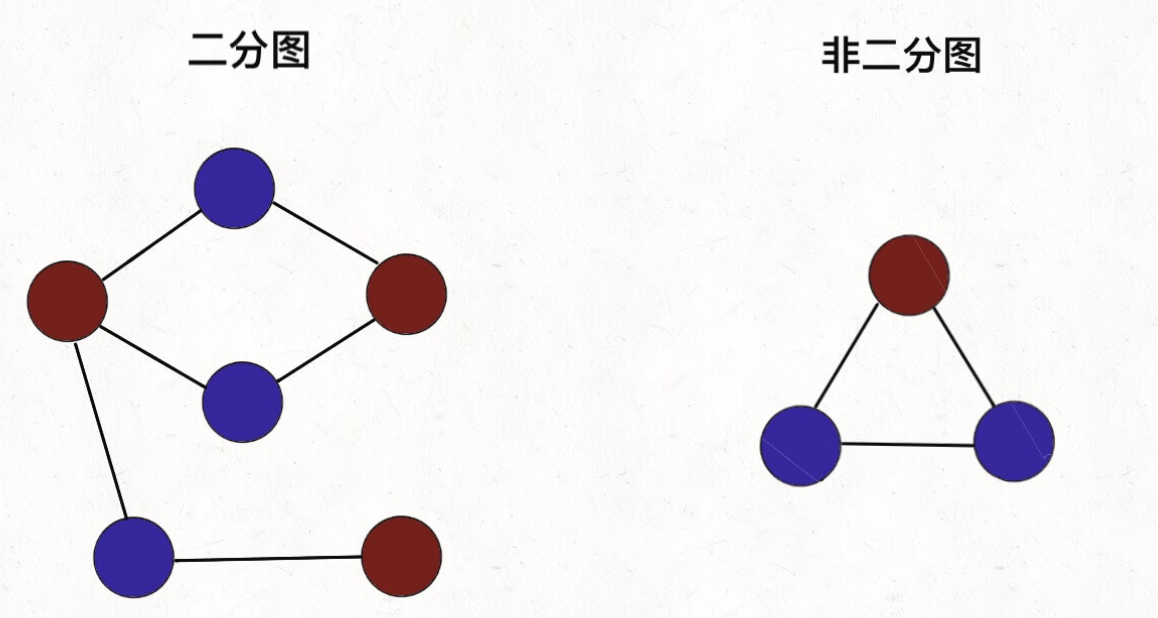
比如两个子集，一个是男、另一个是女，或者一个是岗位、另一个是求职者。

二分图结构在某些场景可以更高效地存储数据，举例来说，如何存储电影演员和电影之间的关系？如果用哈希表存储，需要两个哈希表分别存储「每个演员到电影列表」的映射和「每部电影到演员列表」的映射。但如果用「图」结构存储，将电影和参演的演员连接，很自然地就成为了一幅二分图——每个电影节点的相邻节点就是参演该电影的所有演员，每个演员的相邻节点就是该演员参演过的所有电影。

相关算法

二分图的判定和划分——染色法，可通过图遍历（DFS或BFS）或并查集实现。

实现上很简单，见785.二分图判定和划分。代码实现如下：

  1 //染色法，每个节点与其邻接节点颜色都不同。法1：图遍历（DFS、BFS）；法2：并查集
  2 class Solution {//输入数据未邻接表存储的图
  3 
  4     //利用并查集。因二分图每个节点颜色与其所有邻接节点相反，故对于一个节点，将其所有邻接节点归为一类；对每个节点执行该操作，如果执行过程中发现节点与其邻接节点连通则说明不是二分图
  5     public boolean isBipartite(int[][] graph) {
  6         int n=graph.length;
  7         UF uf=new UF(n);
  8         for(int i=0;i<n;i++){
  9             for(int j=1;j<graph[i].length;j++){
 10                 uf.union(graph[i][0], graph[i][j]);
 11                 if(uf.connected(i,graph[i][0])){
 12                     return false;
 13                 }
 14             }
 15         }
 16         return true;
 17     }
 18 //假定方法参数指定的元素都在并查集中存在。最好须保证更方法幂等
 19 class UF {
 20     // 连通分量个数
 21     private int count;
 22     // 存储某个树节点的父节点
 23     private int[] parent;
 24     // 记录树的节点数：size[x]为以x为根节点的子树的节点数
 25     private int[] size;
 26 
 27     public UF(int n) {
 28         this.count = n;
 29         parent = new int[n];
 30         size = new int[n];
 31         for (int i = 0; i < n; i++) {
 32             parent[i] = i;
 33             size[i] = 1;
 34         }
 35     }
 36 
 37     public void union(int p, int q) {
 38         int rootP = find(p);
 39         int rootQ = find(q);
 40         if (rootP == rootQ)
 41             return;
 42 
 43         // 小树接到大树下面，较平衡
 44         if (size[rootP] > size[rootQ]) {
 45             parent[rootQ] = rootP;
 46             size[rootP] += size[rootQ];
 47         } else {
 48             parent[rootP] = rootQ;
 49             size[rootQ] += size[rootP];
 50         }
 51         count--;
 52     }
 53 
 54     public boolean connected(int p, int q) {
 55         int rootP = find(p);
 56         int rootQ = find(q);
 57         return rootP == rootQ;
 58     }
 59 
 60     public int find(int x) {
 61         while (parent[x] != x) {
 62             // 路径压缩法1
 63             parent[x] = parent[parent[x]];
 64            // 路径压缩法2，更激进的路径压缩
 65             //parent[x] = find(parent[x]);
 66             x = parent[x];
 67         }
 68         return x;
 69     }
 70 
 71     public int count() {
 72         return count;
 73     }
 74 }
 75 
 76 
 77 
 78 
 79     /** 根据给的的图的邻接矩阵或邻接表进行DFS或BFS遍历 */
 80     public boolean isBipartite2(int[][] graph) {
 81         int n = graph.length;
 82         int[] visited = new int[n];
 83         for(int i=0;i<n;i++){ visited[i]=0; }//0表示未染色，1、-1分别表示两种颜色
 84         
 85         for (int i = 0; i < n; i++) {
 86             //if (visited[i]==0 && !bfs(graph, i, visited)) {
 87             if (visited[i]==0 && !dfs(graph, i, 1, visited)) {
 88                 return false;
 89             }
 90         }
 91         return true;
 92     }
 93 
 94     /** 根据给定的图的邻接表和起始节点进行BFS遍历 */
 95     public boolean bfs(int[][] graph, int i, int[] visited) {
 96         Queue<Integer> queue = new LinkedList<>();
 97         visited[i] = 1;
 98         queue.offer(i);
 99         while (!queue.isEmpty()) {
100             i = queue.poll();
101             for (int k = 0; k < graph[i].length; k++) {
102                 int j = graph[i][k];
103                 if (visited[j]==0) {
104                     visited[j] = -visited[i];
105                     queue.offer(j);
106                 }else if(visited[j]==visited[i]){
107                     return false;
108                 }
109             }
110         }
111         return true;
112     }
113 
114     /** 根据给定的图的邻接表和起始节点进行DFS遍历 */
115     public boolean dfs(int[][] graph, int i, int color, int[] visited) {
116         visited[i] = color;
117         for (int k = 0; k < graph[i].length; k++) {
118             int j = graph[i][k];
119             if (visited[j]==0) {
120                 if(!dfs(graph, j, -color, visited)){
121                     return false;
122                 }
123             }else if(visited[j]==visited[i]){
124                 return false;
125             }
126         }
127         return true;
128     }
129 
130 
131 
132 
133 
134     //法1，DFS。self
135     public boolean isBipartite1(int[][] graph) {
136         int n=graph.length;
137         NodeColor[] nodeColor=new NodeColor[n];
138         boolean[][] visited=new boolean[n][n];
139 
140 
141         return dfsDrawColor(graph,nodeColor,visited);
142 
143     }
144     public enum NodeColor{
145         RED, WHITE;
146     }
147 
148     //输入中允许有多个连通分量且允许只有一个节点的连通分量（即孤立节点）
149     public boolean dfsDrawColor(int[][]graph, NodeColor[] nodeColor, boolean[][]visited){
150         boolean res=true;
151         //对每个连通分量染色
152         for(int i=0;i<graph.length;i++){
153             if(nodeColor[i]==null){
154                 res = res && dfsDrawColor(graph,i,NodeColor.RED,nodeColor,visited);
155             }
156         }
157         return res;
158     }
159     //从指定节点开始判断每个节点是否与其各邻接节点反色，递归对各邻接节点执行该过程。指定节点或其各邻接节点都有可能尚未染色，在判断的过程中给节点染色。
160     //指定的起始节点可能是孤立节点
161     public boolean dfsDrawColor(int[][] graph, int i, NodeColor color, NodeColor[] nodeColor, boolean[][]visited){
162         if(nodeColor[i]==null){
163             nodeColor[i]=color;
164             visited[i][i]=true;
165         }
166         NodeColor adjColor= (color==NodeColor.RED)?NodeColor.WHITE:NodeColor.RED;
167         for(int node: graph[i]){
168             if(visited[i][node]){
169                 continue;
170             }
171             if(nodeColor[node]==null){
172                 nodeColor[node]=adjColor;
173             }
174             visited[i][node]=true;
175             visited[node][i]=true;
176             if( nodeColor[node]==color || ( !dfsDrawColor(graph,node,adjColor,nodeColor,visited))){
177                 return false;
178             }
179         }
180         return true;
181     }
182 }
邻接表存储的图的二分判断和划分

二分图的最大匹配/最大独立集——匈牙利算法

二分图的稳定匹配——Gale-Shapley 算法或称“延迟认可算法”，通俗易懂的介绍见Matrix67的介绍。应用：婚姻稳定匹配、岗位匹配等。

 

网络流算法

 

图的连通分量

如何求有向图的强连通分量？一遍DFS或BFS即可得到一个连通分量/强连通分量。

对于有向图，有专门的Tarjan算法、Kosaraju算法，用于在线性时间内寻找一个有向图中的连通分量、割点、桥（割边）、最近公共祖先（LCA）等。它们都是基于DFS遍历的改造，时间复杂度与前面遍历一节所述的一样，但通常Tarjan算法比Kosaraju算法时间效率高。

注：该算法比较简单，但非竞赛的话不掌握也可。

 

posted @ 2017-05-09 15:49  March On  阅读(1539)  评论(0)  编辑  收藏  举报
top last
Welcome user from
(since 2020.6.1)