数据结构_树与二叉树总结
1、树
注:二叉树的所有问题,就是让你在前中后序位置注入巧妙的代码逻辑,去达到自己的目的!!
定义
具有n(n≥)个节点的有穷集合D与D上的关系集合R构成的结构T。即T:=(D,R)。
树的逻辑表示法:树形表示、文氏图表示、凹入表示、嵌套括号表示。
有序树、无序树。
基本概念
双亲节点、祖先节点、兄弟节点、孩子节点、子孙节点
节点的度、树的度、节点的层次、树的深度或称高度。(层次、深度从1起)
根节点、叶子节点(度为0的节点)、分支节点(度非0的节点)、内部节点(非根分支节点)
性质
对于度为k的树:
1、节点数=度数+1
2、第i层最多节点数:k(i-1),i≥1
3、高为i的k叉树节点数最多:(ki-1)/(k-1),i≥1
4、n个节点的k叉树深度最小为:ceil( logk( n(k-1)+1 ) )
存储结构
多重链表:定长链节点个数(二叉树等)、不定长链节点个数
三重链表:每个节点三个指针域(第一个孩子节点、双亲节点、第一个兄弟节点)
对树的操作
构建、遍历、销毁;插入某节点、查找某节点、删除某节点
2、二叉树
二叉树是有序树,有5中基本形态。(度不超过2的树不一定是二叉树,因为二叉树还要求左右子树有序不能颠倒)
n个节点可以构建卡特兰数 f(n)= (k=1~n)Σ(f(k-1)f(n-k)) = (C2n n)/(n+1) ,f(0)=f(1)=1种形态的二叉树。对于有n个节点的有序序列,其BST树也是卡特兰数种。
性质
1、节点数=度数+1
2、第i层节点数:2(i-1),i≥1
3、高为i的二叉树节点数最多:2i-1,i≥1
4、n个节点的二叉树深度最小为:ceil( log2(n+1) ),为理想平衡二叉树时取最小值
5、度为0的节点数=度为2的节点数+1。(因为 节点数n=n0+n1+n2 且 分支数 n-1=n1+2n2,联立可得之)
6、n个节点的完全二叉树从1起对节点从上到下从左到右的编号,编号为i的节点:父节点编号为 floor(i/2),除非该节点已为父节点;左孩子节点编号为2i,除非2i>n即该节点已为叶子节点;右孩子编号为2i+1,除非2i+1>n即右孩子不存在。
推而广之,对于完全m叉树编号为i的节点,其父节点编号为 floor((i+m-2)/m ) ,第j个孩子编号为 mi+j-m+1 。
存储
1、顺序存储:数组。(适用于完全二叉树的存储,一般二叉树可以通过填充虚拟节点当成完全二叉树来存储。缺点是浪费空间)
2、链式存储:
二叉链表(左孩子、右孩子):n个节点的二叉树有n+1个空指针域(空指针域即2n0+n1=n2+1+n0+n1=n+1)。线索二叉树通过利用空指针域指向直接前驱、后继节点来避免遍历时使用堆栈,如中序线索二叉树。
三叉链表(父节点、左孩子、右孩子)
建立
建立:根据输入的序列构建用二叉链表存储的二叉树。这里假定序列为字符串,每个字符对应树中一个节点。
遍历:根据输入序列构建二叉树时需要遍历输入序列,遍历方式有:前序遍历、中序遍历、后序遍历、层次遍历,具体下节介绍。
输入:
首先说下补空,由输入序列(前缀、中缀、后缀皆可)构建二叉树时,如果序列里没有标记一些节点结束信息,则由于无法识别结束或哪些是叶节点从而不能由序列构建出树。所谓补空就是在序列中加入一些特殊字符如'#',加在哪?方式1:通常是序列对应的树的节点的空指针域中,也即度为1和0的节点的空孩子,此时对于n个节点的序列其补空数为n+1;方式2:也可以只对度为1的节点补空。有趣的是如果输入序列是表达式,则用前种补空方式时只有叶节点即操作数补空、用后种补空时没有节点被补空。通常用前种方式补空,某些特殊情况下才用后者。
加括号:把根节点和其左右子树看成一体,在其外围加上括号。左右子树都不存在的节点(叶节点)不用加括号。
百言不如一图,树T按方式1、2分别被补空为T1、T2:

对输入序列:由单一序列就想构建二叉树则需要 序列包含补空信息 或 序列本身包含额外信息(如前缀表达式序列操作符为内部节点操作数为叶节点),要想不补空就能构建二叉树则需多个序列。
总结:(带括号补空:前、中、后序递归; 不带括号补空:前序递归、后序非递归、层次非递归; 不带括号不补空:前后缀表达式、前中序、中后序、中序层次 等),其中,由 不带括号内补空层次序列 构建二叉树最直观最适用,如LeetCode中与树有关的题目的输入。
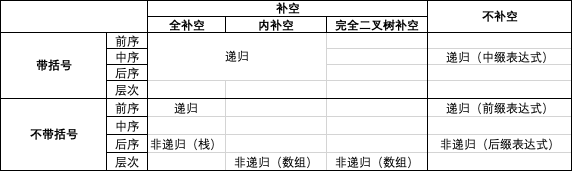
1、通常而言,输入序列里需要包含补空信息,此时可采用 前序、中序、后序 遍历输入序列来建立二叉树,只要构建过程遍历采用的序与输入序列采用的序一样。分为两种情况:
1)带括号的补空序列(方式1或2)(可按方式1或2补空,不管是T1、T2,有几个内部节点就有几个括号,即为T的节点数或内部节点数)
a、带括号、补空,前序序列(递归构建):

1 void createPreOrder_withBrackets(char prefix[],BTREE &T) 2 { 3 //要求输入的前缀序列带括号 ,并含有对度为0和1的节点的补空特殊字符。此时非特殊字符都成了“内部节点”,有几个非特殊字符就有几个括号。 4 //当然也可以只对度为1的补空,此时有几个非叶节点的非特殊字符就有几个括号。若输入的是前缀表达式,则此情况的内部节点其实就是操作符,叶节点是操作数。 5 //例子:度为0和1的补空:( A( B( D##) ( E( G#( H##) ) #) ) ( C( F##) #) ),只对度为1的补空:( A( BD( E( G#H )# ) )( CF# ) ) 6 //特殊例子(前缀表达式):度为0和1的补空:( *( +( A##) ( /( -( B##) ( C##) ) ( D##) ) ) ( E##) ) ,只对度为1的补空:(*(+A(/(-BC)D))E) 7 char x=nextToken(prefix); 8 9 if(x=='#') 10 { 11 T=NULL; 12 } 13 else 14 { 15 T=(BTREE)malloc(sizeof(BTNode)); 16 T->lchild=NULL; 17 T->rchild=NULL; 18 19 if(x=='(') 20 {//处理括号里的表达式 21 x=nextToken(prefix);//表达式的操作符 22 T->data=x; 23 24 createPreOrder_withBrackets(prefix,T->lchild);//表达式的左操作数 25 26 createPreOrder_withBrackets(prefix,T->rchild);//表达式的右操作数 27 28 nextToken(prefix);//右括号 29 } 30 else 31 { 32 T->data=x; 33 } 34 } 35 }
若输入按方式1补空,则括号数为T1的内部节点数即T的节点数,如 ( *( +( A##) ( /( -( B##) ( C##) ) ( D##) ) ) ( E##) ) 、 ( A( B( D##) ( E( G#( H##) ) #) ) ( C( F##) #) ) ;
若输入按方式2补空,则括号数为T2的内部节点数即T的内部节点数。如 (*(+A(/(-BC)D))E) 、 ( A( BD( E( G#H )# ) )( CF# ) ) ,可以发现前者就是前缀表达式,只不过多了括号。
可以发现,不论哪种补空方式,括号数都是补空后的树的内部节点数。想想,表达式树的内部节点都是操作符叶节点都是操作数,其中缀表达式的括号数就是操作符(内部节点)数,与这里的括号数有何联系?(answer:表达式树没有度为1的节点,故相当于内补空树)
b、带括号、补空,中序序列(递归构建):与上类似,改变一行代码顺序即可。
c、带括号、补空,后序序列(递归构建):同样,改变一行代码顺序即可。
输入示例:
|--------------------------------------------------------------------------------------------------------------------------------------------|
| 方式1:度为1、0的节点补空 | 方式2:度为1的节点补空 |
| 前缀:( *( +( A##) ( /( -( B##) ( C##) ) ( D##) ) ) ( E##) ) | (*(+A(/(-BC)D))E) |
| 示例1 中缀:( ( ( #A#) +( ( ( #B#) -( #C#) ) /( #D#) ) ) *( #E#) ) | ((A+((B-C)/D))*E) |
| 后缀:(((##A)(((##B)(##C)-)(##D)/)+)(##E)*) | ((A((BC-)D/)+)E*) |
|---------------------------------------------------------------------------------------------------------------------------------------------|
| 前缀:( A( B( D##) ( E( G#( H##) ) #) ) ( C( F##) #) ) | ( A( BD( E( G#H )# ) )( CF# ) ) |
| 示例2 中缀:( ( ( #D#) B( ( #G( #H#) ) E#) ) A( ( #F#) C#) ) | ( ( DB( ( #GH )E# ) )A( FC# ) ) |
| 后缀:(((##D)((#(##H)G)#E)B)((##F)#C)A) | ( ( D( ( #HG )#E )B )( F#C )A ) |
|_____________________________________________________________________________________|
可以发现,此种方法能对带括号的中缀表达式构建表达式树。
2)不带括号的补空序列(只能方式1)。实际上本方式使用得最多,加括号是为了程序解析但不利于人阅读,括号数一多不信你不会被搞蒙。。。
a、不带括号、全补空、前序序列(递归构建):

1 void createPreOrder(char prefixStr[],BTREE &T) 2 { 3 char x=nextToken(prefixStr); 4 if(x=='#') 5 { 6 T=NULL; 7 } 8 else 9 { 10 T=(BTREE)malloc(sizeof(BTNode)); 11 T->data=x; 12 createPreOrder(prefixStr,T->lchild); 13 createPreOrder(prefixStr,T->rchild); 14 } 15 }
输入示例(上表第一列前序者去掉括号即可): +A##/-B##C##D##E## 、 AB D## E G# H### C F## #
b、不带括号,全补空、中序序列,可以发现参数不管什么中序序列补空后每个字符左右均为#,所以其对应的树不唯一,故不带括号的中序补空序列没法构建树。
c、不带括号、全补空、后序序列(非递归构建):每遇到一个非补空字符时为之创建一个新节点并从栈中取两个节点作为其孩子

1 void createPostOrder(char infix[],BTREE &T) 2 {// 3 int stackSize=100; 4 BTREE stack[stackSize],p; 5 int top=-1; 6 char x; 7 while(1) 8 { 9 x=nextToken(infix); 10 if(x=='\0') 11 { 12 break; 13 } 14 else if(x=='#') 15 { 16 stack[++top]=NULL; 17 } 18 else 19 { 20 p=(BTREE)malloc(sizeof(BTNode)); 21 p->data=x; 22 p->lchild=stack[top-1];; 23 p->rchild=stack[top]; 24 stack[top-1]=p; 25 top--; 26 } 27 } 28 T=stack[0]; 29 }
输入示例(上表第一列后序者去掉括号即可)
d、不带括号、按完全二叉树形式补空、层次遍历序列(非递归构建)

1 void createLayerOrder(char layerSeq[],int n,BTREE &T) 2 {//输入序列是广度优先序列,且按完全二叉树形式补空,因为要利用父子节点间编号的关系。如 "12#34#####5" 3 if(n<0) return; 4 5 BTREE node[n]; 6 int i,j; 7 for(i=0;i<n;i++) 8 { 9 if(layerSeq[i]!='#') 10 { 11 node[i]=(BTREE)malloc(sizeof(BTNode)); 12 node[i]->data=layerSeq[i]; 13 node[i]->lchild=NULL; 14 node[i]->rchild=NULL; 15 if(i==0) 16 { 17 T=node[i]; 18 } 19 else 20 { 21 j=(i-1)/2;//父节点下标 22 if(2*j+1==i)node[j]->lchild=node[i];//当前节点是父节点的左孩子 23 else node[j]->rchild=node[i] ;//当前节点是父节点的右孩子 24 } 25 } 26 } 27 }
e、不带括号、内补空、层次序列,最直接最常用
将内补空序列转为完全二叉树形式补空序列,然后按d处理或直接在转换的过程中建立:

1 //输入层次遍历序列(内补空),构建二叉树 2 void createLayerOrder2(char layerSeq[],int n,BTREE &T) 3 { 4 //先将序列转为完全二叉树形式补空的序列 5 const int M=100; 6 7 if(n<=0) return; 8 9 char input[M];//node[]用于以完全二叉树形式存储节点 10 BTREE node[M]; 11 12 int i=0,nonBlank=0; 13 while(i<n) 14 {//统计非空字符数,作为下面循环结束的条件 15 input[i]=layerSeq[i]; 16 if(input[i]!='#') 17 { 18 nonBlank++; 19 } 20 i++; 21 } 22 23 i=0; 24 int j; 25 while(nonBlank>0) 26 { 27 if(input[i]!='#') 28 { 29 nonBlank--; 30 {//法1,转换为完全二叉树补空形式过程中构建 31 node[i]=(BTREE)malloc(sizeof(BTNode)); 32 node[i]->data=input[i]; 33 node[i]->lchild=NULL; 34 node[i]->rchild=NULL; 35 if(i==0) 36 { 37 T=node[i]; 38 } 39 else 40 { 41 j=(i-1)/2; 42 if(2*j+1==i)node[j]->lchild=node[i]; 43 else if(2*j+2==i) node[j]->rchild=node[i]; 44 } 45 } 46 } 47 else 48 { 49 //后移两位 50 for(j=n-1;j>=2*i+1;j--) 51 { 52 input[j+2]=input[j]; 53 } 54 n+=2; 55 input[2*i+1]='#'; 56 input[2*i+2]='#'; 57 } 58 i++; 59 } 60 61 62 {//法2,调用,根据完全二叉树形式补空序列构建二叉树 63 // input[n]='\0'; 64 // printf("%s\n",input); 65 // createLayerOrder(input,n,T) ;//输入二叉树形式补空的序列,构建二叉树 66 } 67 }
2、要想输入时不需补空:
1)要么同时提供中序、前序序列 或 同时提供中序、后序序列 或 同时提供中序、层次序列。
法一(三种均可用此法):根据中序序列下标采用逐点插入法构建“二叉搜索树”——前序、层次序列从头到尾各元素依次插入;后序序列从后到前各元素依次插入。

1 //根据 中序序列 和 后序|前序|层次序列 构建二叉树。采用逐点插入法构建“二叉搜索树”。 2 int cbiGetIndex(char inorder[],int n,char val) 3 {//获取给定值在中序序列的下标 4 int i=0; 5 while(i<n && inorder[i]!=val) 6 { 7 i++; 8 } 9 return i; 10 } 11 void cbiBuildBST(BTREE &T,char inorder[],int n,char val) 12 {//插入一个值到二叉搜索树 13 if(T==NULL) 14 { 15 T=(BTREE)malloc(sizeof(BTNode)); 16 T->data=val; 17 T->lchild=NULL; 18 T->rchild=NULL; 19 } 20 else if(cbiGetIndex(inorder,n,val) < cbiGetIndex(inorder,n,T->data)) 21 { 22 cbiBuildBST(T->lchild,inorder,n,val); 23 } 24 else 25 { 26 cbiBuildBST(T->rchild,inorder,n,val); 27 } 28 } 29 void createByInAndOtherOrder(BTREE &T,char input[],int isInputPostOrder,char inorder[],int n) 30 {//根据 中序序列 和 后序|前序|层次序列 构建二叉树。采用逐点插入法构建“二叉搜索树”。 31 printf("%s %d\n",input,n); 32 int i; 33 if(isInputPostOrder) 34 {//若input是后序序列,从后往前依次插入各元素 35 for(i=n-1;i>=0;i--) 36 { 37 cbiBuildBST(T,inorder,n,input[i]); 38 } 39 } 40 else{//否则input是前序或后序序列,从前往后依次插入各元素 41 for(i=0;i<n;i++) 42 { 43 cbiBuildBST(T,inorder,n,input[i]); 44 } 45 } 46 }
法二(前两种可用此法):取前序序列首元素,找到在中序序列的位置,此位置分割成的左右两部分就是左子树和右子树,两部分的长度分别对应前序序列接下来两部分的长度,递归进行。
a、由前序、中序序列构建二叉树:(不带括号、不补空、递归构建)。

1 //由前序、中序序列(不补空不带括号)构建二叉树。有重复元素的话树不唯一,所以不能有重 2 void createByPreInOrder(BTREE &T,char preorder[],int preStart,int preEnd,char inorder[],int inStart,int inEnd) 3 {//求前序序列首元素在中序序列的位置,此位置左边为左子树序列、右边为右子树序列,两者的长度分别对应前序序列接下来的两段长度,接下来递归进行。 4 if(preStart>preEnd || inStart>inEnd || preEnd-preStart!=inEnd-inStart) 5 { 6 return; 7 } 8 9 //求前序序列首元素在中序序列的位置 及 中序序列被该元素分成的左右子序列的长度 10 int pivot; 11 for(pivot=inStart; pivot<=inEnd && preorder[preStart]!=inorder[pivot];pivot++); 12 int leftLen=pivot-inStart;//位置左边的元素个数 13 int rightLen=inEnd-pivot;//位置右边的元素个数 14 15 T=(BTREE)malloc(sizeof(BTNode)); 16 T->data=preorder[preStart]; 17 T->lchild=NULL; 18 T->rchild=NULL; 19 if(leftLen>0) 20 { 21 createByPreInOrder(T->lchild,preorder, preStart+1, preStart+1+leftLen-1, inorder, inStart, pivot-1); 22 } 23 if(rightLen>0) 24 { 25 createByPreInOrder(T->rchild,preorder, preStart+1+leftLen, preEnd, inorder, pivot+1, inEnd); 26 } 27 }
b、由后序、中序序列构建二叉树:(不带括号、不补空、递归构建)。与上述类似,只不过每次取的是后序序列的末尾值来构建新节点

1 //由后序、中序序列(不补空不带括号)构建二叉树。有重复元素的话树不唯一,所以不能有重 2 void createByPostInOrder(BTREE &T,char postorder[],int postStart,int postEnd,char inorder[],int inStart,int inEnd) 3 {//求后序序列末元素在中序序列的位置,此位置左边为左子树序列、右边为右子树序列,两者的长度分别对应后序序列从首元素开始的两段长度,接下来递归进行。 4 if(postStart>postEnd || inStart>inEnd || postEnd-postStart!=inEnd-inStart) 5 { 6 return; 7 } 8 9 //求前序序列首元素在中序序列的位置 及 中序序列被该元素分成的左右子序列的长度 10 int pivot; 11 for(pivot=inStart; pivot<=inEnd && postorder[postEnd]!=inorder[pivot];pivot++); 12 int leftLen=pivot-inStart; 13 int rightLen=inEnd-pivot; 14 15 T=(BTREE)malloc(sizeof(BTNode)); 16 T->data=postorder[postEnd]; 17 T->lchild=NULL; 18 T->rchild=NULL; 19 if(leftLen>0) 20 { 21 createByPostInOrder(T->lchild,postorder, postStart, postStart+leftLen-1, inorder, inStart, pivot-1); 22 } 23 if(rightLen>0) 24 { 25 createByPostInOrder(T->rchild,postorder, postStart+leftLen, postEnd-1, inorder, pivot+1, inEnd); 26 } 27 }
注意:
若提供了二叉查找树的后序遍历序列则即可构建出该树,因为二叉查找树的中序序列是递增的,我们可以从后序序列得到中序序列;实际上,不获取也可,从后往前依次将每个元素插入即可。(给定BST的前序序列时与此类似)。此时实际上是上述法一的特殊情况。此外,如果定义了元素大小关系,则实际上给定任意序列都可以构建出二叉查找树,树的形状(与输入序列、与从序列后往前或从前往后插入到BST顺序)有关,构建算法可以是递归、非递归的(有关BST的建立、查找、删除见后文‘特殊二叉树’一节)。
2)要么序列本身包含额外信息:如前缀表达式或后缀表达式因操作符为内部节点操作数为叶节点,可直接根据序列构建表达式树;带括号的中缀表达式(每个运算符都有对应的括号)括号能提供额外信息,因此也能直接根据之建立树。表达式树由非叶节点(即操作符)都有左右孩子,故相当于进行了内补空。
由表达式序列构建表达式树示例:由表达式序列构建表达式树-MarchOn (前缀、中缀递归,后缀非递归)
a、前缀表达式序列构建表达式树(不带括号、递归构建):

1 void createPrefix_recursive(char prefix[],BTREE &T) 2 {//递归方式_由前缀表达式构建表达式树,输入示例:*+A/-BCDE 3 char x=nextToken(prefix); 4 5 T=(BTREE)malloc(sizeof(BTNode)); 6 T->data=x; 7 T->lchild=NULL; 8 T->rchild=NULL; 9 10 if(!isOpNum(x))//是操作符。前缀表达式的最后一个字符一定是操作数,所以下面的递归会停止。 11 { 12 createPrefix_recursive(prefix,T->lchild); 13 createPrefix_recursive(prefix,T->rchild); 14 } 15 }
输入示例: *+A/-BCDE
b、中缀表达式序列构建表达式树(带括号、递归构建):直接用带括号补空的方法(1、1、b)中的方法。不过由于表达式树内部节点为操作符叶子节点为操作数不存在为度为1的节点,所以构建方法可以稍微简化:

1 void createInfix_recursive(char infix[],BTREE &T) 2 {//递归方式_由中缀表达式构建表达式树,要求输入的中缀表达式加括号,有几个操作数就几个括号 3 char x=nextToken(infix); 4 5 T=(BTREE)malloc(sizeof(BTNode)); 6 T->lchild=NULL; 7 T->rchild=NULL; 8 9 if(x=='(') 10 {//处理括号里的表达式 11 createInfix_recursive(infix,T->lchild);//表达式的左操作数 12 13 x=nextToken(infix);//表达式的操作符 14 T->data=x; 15 16 createInfix_recursive(infix,T->rchild);//表达式的右操作数 17 nextToken(infix);//右括号 18 } 19 else 20 { 21 T->data=x; 22 } 23 }
输入示例: ((A+((B-C)/D))*E)
c、后缀表达式序列构建表达式树(不带括号、非递归构建):

1 #define M 100 2 void createPostfix_nonrecursive(char postfix[],BTREE &T) 3 {//非递归方式_由后缀表达式构建表达式树 4 BTREE stack[M],p; 5 int top=-1; 6 char x; 7 while(1) 8 { 9 x=nextToken(postfix); 10 if(x=='\0') 11 { 12 break; 13 } 14 15 p=(BTREE)malloc(sizeof(BTNode)) ; 16 p->data=x; 17 p->lchild=NULL; 18 p->rchild=NULL; 19 20 if(isOpNum(x)) 21 {//操作数 22 stack[++top]=p; 23 } 24 else 25 {//操作符 26 p->lchild=stack[top-1]; 27 p->rchild=stack[top]; 28 stack[top-1]=p; 29 top--; 30 } 31 } 32 T=stack[0]; 33 }
输入示例: ABC-D/+E*
这里总结了根据不同输入形式构建二叉树的方法,当遇到不是这些形式的时,可以向这些形式靠。如A( (B ( D,E(G)), C(F(,H) ) ) )
但是,也不要那么死板局限于这里的方法,条条大路通罗马,肯定还会有其他方法的。
附:上述关于树创建的完整代码:

1 #include<stdio.h> 2 #include<malloc.h> 3 typedef struct node 4 { 5 int data; 6 struct node* lchild; 7 struct node* rchild; 8 }BTNode,*BTREE; 9 10 11 //遍历 12 13 void searchPrefix(BTREE T) 14 { 15 if(T!=NULL) 16 { 17 printf("%c",T->data); 18 19 searchPrefix(T->lchild); 20 21 searchPrefix(T->rchild); 22 } 23 } 24 void searchInfix(BTREE T) 25 { 26 if(T!=NULL) 27 {//访问到内部节点时左右加括号 ,因此几个内部节点就有几个括号,如果树是表达式树 ,则得到了带括号的中缀表达式 28 // if(T->lchild!=NULL || T->rchild!=NULL){ printf("( "); } 29 searchInfix(T->lchild); 30 // if((T->lchild!=NULL || T->rchild!=NULL) && (T->lchild==NULL)){ printf("#"); }//内部节点的空孩子用特殊符号代替 31 32 printf("%c",T->data); 33 34 searchInfix(T->rchild); 35 // if((T->lchild!=NULL || T->rchild!=NULL) && (T->rchild==NULL)){ printf("#"); }//内部节点的空孩子用特殊符号代替 36 // if(T->lchild!=NULL || T->rchild!=NULL){ printf(" )"); } 37 } 38 } 39 void searchPostfix(BTREE T) 40 { 41 if(T!=NULL) 42 {//访问到内部节点时左右加括号 ,因此几个内部节点就有几个括号,如果树是表达式树 ,则得到了带括号的后缀表达式 43 // if(T->lchild!=NULL || T->rchild!=NULL){ printf("( "); } 44 searchPostfix(T->lchild); 45 // if((T->lchild!=NULL || T->rchild!=NULL) && (T->lchild==NULL)){ printf("#"); }//内部节点的空孩子用特殊符号代替 46 47 searchPostfix(T->rchild); 48 // if((T->lchild!=NULL || T->rchild!=NULL) && (T->rchild==NULL)){ printf("#"); }//内部节点的空孩子用特殊符号代替 49 50 printf("%c",T->data); 51 // if(T->lchild!=NULL || T->rchild!=NULL){ printf(" )"); } 52 } 53 } 54 55 56 //构建 57 char nextToken(char str[]) //读取下一字符,略过空格 58 { 59 static int pos=0; 60 while(str[pos]!='\0' && str[pos]==' '){ pos++; } 61 return str[pos++]; 62 } 63 64 65 void createPreOrder_withBrackets_c(char prefix[],BTREE *T) 66 {//为了能更改T,这里采用了指针,为了更清晰简洁,可以用C++里的引用 67 char x=nextToken(prefix); 68 69 if(x=='#') 70 { 71 *T=NULL; 72 } 73 else 74 { 75 *T=(BTREE)malloc(sizeof(BTNode)); 76 (*T)->lchild=NULL; 77 (*T)->rchild=NULL; 78 79 if(x=='(') 80 {//处理括号里的表达式 81 x=nextToken(prefix);//表达式的操作符 82 (*T)->data=x; 83 84 createPreOrder_withBrackets_c(prefix,&((*T)->lchild));//表达式的左操作数 85 86 createPreOrder_withBrackets_c(prefix,&((*T)->rchild));//表达式的右操作数 87 88 nextToken(prefix);//右括号 89 } 90 else 91 { 92 (*T)->data=x; 93 } 94 } 95 } 96 97 void createPreOrder_withBrackets(char prefix[],BTREE &T) 98 { 99 //要求输入的前缀序列带括号 ,并含有对度为0和1的节点的补空特殊字符。此时非特殊字符都成了“内部节点”,有几个非特殊字符就有几个括号。 100 //当然也可以只对度为1的补空,此时有几个非叶节点的非特殊字符就有几个括号。若输入的是前缀表达式,则此情况的内部节点其实就是操作符,叶节点是操作数。 101 //例子:度为0和1的补空:( A( B( D##) ( E( G#( H##) ) #) ) ( C( F##) #) ),只对度为1的补空:( A( BD( E( G#H )# ) )( CF# ) ) 102 //特殊例子(前缀表达式):度为0和1的补空:( *( +( A##) ( /( -( B##) ( C##) ) ( D##) ) ) ( E##) ) ,只对度为1的补空:(*(+A(/(-BC)D))E) 103 char x=nextToken(prefix); 104 105 if(x=='#') 106 { 107 T=NULL; 108 } 109 else 110 { 111 T=(BTREE)malloc(sizeof(BTNode)); 112 T->lchild=NULL; 113 T->rchild=NULL; 114 115 if(x=='(') 116 {//处理括号里的表达式 117 x=nextToken(prefix);//表达式的操作符 118 T->data=x; 119 120 createPreOrder_withBrackets(prefix,T->lchild);//表达式的左操作数 121 122 createPreOrder_withBrackets(prefix,T->rchild);//表达式的右操作数 123 124 nextToken(prefix);//右括号 125 } 126 else 127 { 128 T->data=x; 129 } 130 } 131 } 132 133 void createInOrder_withBrackets(char infix[],BTREE &T) 134 {//要求输入的序列带括号 ,内部节点才带括号;度为1的节点缺失的孩子补特殊字符(度为0的可补可不补) 135 char x=nextToken(infix); 136 137 if(x=='#') 138 { 139 T=NULL; 140 } 141 else 142 { 143 T=(BTREE)malloc(sizeof(BTNode)); 144 T->lchild=NULL; 145 T->rchild=NULL; 146 147 if(x=='(') 148 {//处理括号里的表达式 149 createInOrder_withBrackets(infix,T->lchild);//表达式的左操作数 150 151 x=nextToken(infix);//表达式的操作符 152 T->data=x; 153 154 createInOrder_withBrackets(infix,T->rchild);//表达式的右操作数 155 156 nextToken(infix);//右括号 157 } 158 else 159 { 160 T->data=x; 161 } 162 } 163 } 164 165 void createPostOrder_withBrackets(char infix[],BTREE &T) 166 {//要求输入的序列带括号 ,内部节点才带括号;度为1的节点缺失的孩子补特殊字符(度为0的可补可不补) 167 char x=nextToken(infix); 168 169 if(x=='#') 170 { 171 T=NULL; 172 } 173 else 174 { 175 T=(BTREE)malloc(sizeof(BTNode)); 176 T->lchild=NULL; 177 T->rchild=NULL; 178 179 if(x=='(') 180 {//处理括号里的表达式 181 createPostOrder_withBrackets(infix,T->lchild);//表达式的左操作数 182 183 createPostOrder_withBrackets(infix,T->rchild);//表达式的右操作数 184 185 x=nextToken(infix);//表达式的操作符 186 T->data=x; 187 188 nextToken(infix);//右括号 189 } 190 else 191 { 192 T->data=x; 193 } 194 } 195 } 196 197 void createPreOrder(char prefixStr[],BTREE &T) 198 {//输入序列为 全补空、不带括号 的序列 199 char x=nextToken(prefixStr); 200 if(x=='#') 201 { 202 T=NULL; 203 } 204 else 205 { 206 T=(BTREE)malloc(sizeof(BTNode)); 207 T->data=x; 208 createPreOrder(prefixStr,T->lchild); 209 createPreOrder(prefixStr,T->rchild); 210 } 211 } 212 213 214 void createPostOrder(char infix[],BTREE &T) 215 {// 输入序列为 全补空、不带括号 的序列 216 int stackSize=100; 217 BTREE stack[stackSize],p; 218 int top=-1; 219 char x; 220 while(1) 221 { 222 x=nextToken(infix); 223 if(x=='\0') 224 { 225 break; 226 } 227 else if(x=='#') 228 { 229 stack[++top]=NULL; 230 } 231 else 232 { 233 p=(BTREE)malloc(sizeof(BTNode)); 234 p->data=x; 235 p->lchild=stack[top-1];; 236 p->rchild=stack[top]; 237 stack[top-1]=p; 238 top--; 239 } 240 } 241 T=stack[0]; 242 } 243 244 //输入层次遍历序列(全补空),构建二叉树 245 void createLayerOrder(char layerSeq[],int n,BTREE &T) 246 {//输入序列是广度优先序列,且按完全二叉树形式补空,因为要利用父子节点间编号的关系。如 "12#34#####5" 247 //构建后的实际节点数≤n 248 if(n<=0) return; 249 250 BTREE node[n]; 251 int i,j; 252 for(i=0;i<n;i++) 253 { 254 if(layerSeq[i]!='#') 255 { 256 node[i]=(BTREE)malloc(sizeof(BTNode)); 257 node[i]->data=layerSeq[i]; 258 node[i]->lchild=NULL; 259 node[i]->rchild=NULL; 260 if(i==0) 261 { 262 T=node[i]; 263 } 264 else 265 { 266 j=(i-1)/2;//父节点下标 267 if(2*j+1==i)node[j]->lchild=node[i];//当前节点是父节点的左孩子 268 else node[j]->rchild=node[i] ;//当前节点是父节点的右孩子 269 } 270 } 271 } 272 } 273 274 //输入层次遍历序列(内补空),构建二叉树 275 void createLayerOrder2(char layerSeq[],int n,BTREE &T) 276 { 277 //先将序列转为完全二叉树形式补空的序列 278 const int M=100; 279 280 if(n<=0) return; 281 282 char input[M];//node[]用于以完全二叉树形式存储节点 283 BTREE node[M]; 284 285 int i=0,nonBlank=0; 286 while(i<n) 287 {//统计非空字符数,作为下面循环结束的条件 288 input[i]=layerSeq[i]; 289 if(input[i]!='#') 290 { 291 nonBlank++; 292 } 293 i++; 294 } 295 296 i=0; 297 int j; 298 while(nonBlank>0) 299 { 300 if(input[i]!='#') 301 { 302 nonBlank--; 303 {//法1,转换为完全二叉树补空形式过程中构建 304 node[i]=(BTREE)malloc(sizeof(BTNode)); 305 node[i]->data=input[i]; 306 node[i]->lchild=NULL; 307 node[i]->rchild=NULL; 308 if(i==0) 309 { 310 T=node[i]; 311 } 312 else 313 { 314 j=(i-1)/2; 315 if(2*j+1==i)node[j]->lchild=node[i]; 316 else if(2*j+2==i) node[j]->rchild=node[i]; 317 } 318 } 319 } 320 else 321 { 322 //后移两位 323 for(j=n-1;j>=2*i+1;j--) 324 { 325 input[j+2]=input[j]; 326 } 327 n+=2; 328 input[2*i+1]='#'; 329 input[2*i+2]='#'; 330 } 331 i++; 332 } 333 334 335 {//法2,调用,根据完全二叉树形式补空序列构建二叉树 336 // input[n]='\0'; 337 // printf("%s\n",input); 338 // createLayerOrder(input,n,T) ;//输入二叉树形式补空的序列,构建二叉树 339 } 340 } 341 342 //由前序、中序序列(不补空不带括号)构建二叉树。有重复元素的话树不唯一,所以不能有重 343 void createByPreInOrder(BTREE &T,char preorder[],int preStart,int preEnd,char inorder[],int inStart,int inEnd) 344 {//求前序序列首元素在中序序列的位置,此位置左边为左子树序列、右边为右子树序列,两者的长度分别对应前序序列接下来的两段长度,接下来递归进行。 345 if(preStart>preEnd || inStart>inEnd || preEnd-preStart!=inEnd-inStart) 346 { 347 return; 348 } 349 350 //求前序序列首元素在中序序列的位置 及 中序序列被该元素分成的左右子序列的长度 351 int pivot; 352 for(pivot=inStart; pivot<=inEnd && preorder[preStart]!=inorder[pivot];pivot++); 353 int leftLen=pivot-inStart;//位置左边的元素个数 354 int rightLen=inEnd-pivot;//位置右边的元素个数 355 356 T=(BTREE)malloc(sizeof(BTNode)); 357 T->data=preorder[preStart]; 358 T->lchild=NULL; 359 T->rchild=NULL; 360 if(leftLen>0) 361 { 362 createByPreInOrder(T->lchild,preorder, preStart+1, preStart+1+leftLen-1, inorder, inStart, pivot-1); 363 } 364 if(rightLen>0) 365 { 366 createByPreInOrder(T->rchild,preorder, preStart+1+leftLen, preEnd, inorder, pivot+1, inEnd); 367 } 368 } 369 370 //由后序、中序序列(不补空不带括号)构建二叉树。有重复元素的话树不唯一,所以不能有重 371 void createByPostInOrder(BTREE &T,char postorder[],int postStart,int postEnd,char inorder[],int inStart,int inEnd) 372 {//求后序序列末元素在中序序列的位置,此位置左边为左子树序列、右边为右子树序列,两者的长度分别对应后序序列从首元素开始的两段长度,接下来递归进行。 373 if(postStart>postEnd || inStart>inEnd || postEnd-postStart!=inEnd-inStart) 374 { 375 return; 376 } 377 378 //求前序序列首元素在中序序列的位置 及 中序序列被该元素分成的左右子序列的长度 379 int pivot; 380 for(pivot=inStart; pivot<=inEnd && postorder[postEnd]!=inorder[pivot];pivot++); 381 int leftLen=pivot-inStart; 382 int rightLen=inEnd-pivot; 383 384 T=(BTREE)malloc(sizeof(BTNode)); 385 T->data=postorder[postEnd]; 386 T->lchild=NULL; 387 T->rchild=NULL; 388 if(leftLen>0) 389 { 390 createByPostInOrder(T->lchild,postorder, postStart, postStart+leftLen-1, inorder, inStart, pivot-1); 391 } 392 if(rightLen>0) 393 { 394 createByPostInOrder(T->rchild,postorder, postStart+leftLen, postEnd-1, inorder, pivot+1, inEnd); 395 } 396 } 397 398 //根据 中序序列 和 后序|前序|层次序列 构建二叉树。采用逐点插入法构建“二叉搜索树”。 399 int cbiGetIndex(char inorder[],int n,char val) 400 {//获取给定值在中序序列的下标 401 int i=0; 402 while(i<n && inorder[i]!=val) 403 { 404 i++; 405 } 406 return i; 407 } 408 void cbiBuildBST(BTREE &T,char inorder[],int n,char val) 409 {//插入一个值到二叉搜索树 410 if(T==NULL) 411 { 412 T=(BTREE)malloc(sizeof(BTNode)); 413 T->data=val; 414 T->lchild=NULL; 415 T->rchild=NULL; 416 } 417 else if(cbiGetIndex(inorder,n,val) < cbiGetIndex(inorder,n,T->data)) 418 { 419 cbiBuildBST(T->lchild,inorder,n,val); 420 } 421 else 422 { 423 cbiBuildBST(T->rchild,inorder,n,val); 424 } 425 } 426 void createByInAndOtherOrder(BTREE &T,char input[],int isInputPostOrder,char inorder[],int n) 427 {//根据 中序序列 和 后序|前序|层次序列 构建二叉树。采用逐点插入法构建“二叉搜索树”。 428 printf("%s %d\n",input,n); 429 int i; 430 if(isInputPostOrder) 431 {//若input是后序序列,从后往前依次插入各元素 432 for(i=n-1;i>=0;i--) 433 { 434 cbiBuildBST(T,inorder,n,input[i]); 435 } 436 } 437 else{//否则input是前序或后序序列,从前往后依次插入各元素 438 for(i=0;i<n;i++) 439 { 440 cbiBuildBST(T,inorder,n,input[i]); 441 } 442 } 443 } 444 445 //二叉查找树创建、查找、删除(递归、非递归) 446 void insertBinarySearchTree_nonrecursive(BTREE &T,char item) 447 { 448 BTREE p,q; 449 p=(BTREE)malloc(sizeof(BTNode)); 450 p->data=item; 451 p->lchild=NULL; 452 p->rchild=NULL; 453 if(T==NULL) T=p; 454 else 455 { 456 q=T; 457 while(1) 458 { 459 if(item < q->data) 460 { 461 if(q->lchild!=NULL) q=q->lchild; 462 else 463 { 464 q->lchild=p; 465 break; 466 } 467 } 468 else 469 { 470 if(q->rchild!=NULL) q=q->rchild; 471 else 472 { 473 q->rchild=p; 474 break; 475 } 476 } 477 } 478 } 479 } 480 void insertBinarySearchTree_recursive(BTREE &T,char item) 481 { 482 if(T==NULL) 483 { 484 T=(BTREE)malloc(sizeof(BTNode)); 485 T->data=item; 486 T->lchild=NULL; 487 T->rchild=NULL; 488 } 489 else if(item< T->data) 490 { 491 insertBinarySearchTree_recursive(T->lchild,item); 492 } 493 else 494 { 495 insertBinarySearchTree_recursive(T->rchild,item); 496 } 497 } 498 499 BTREE searchBinarySearchTree_nonrecursive(BTREE T,char item) 500 { 501 if(T==NULL) 502 return NULL; 503 BTREE p=T; 504 while(p!=NULL) 505 { 506 if(p->data==item) 507 return p; 508 else if(p->data<item) 509 p=p->lchild; 510 else 511 p=p->rchild; 512 } 513 } 514 515 BTREE searchBinarySearchTree_recursive(BTREE T,char item) 516 { 517 if(T==NULL || T->data==item) 518 return T; 519 else if(T->data < item) 520 searchBinarySearchTree_recursive(T->lchild,item); 521 else 522 searchBinarySearchTree_recursive(T->rchild,item); 523 } 524 525 void deleteBSTNode(BTREE &T,char key) 526 {//删除二叉查找树中的一个节点。也可以借助后序非递归遍历来实现 ,此时栈顶元素存在的话为当前节点的父节点 527 if(T==NULL)return; 528 else if(key<T->data)deleteBSTNode(T->lchild,key); 529 else if(key>T->data)deleteBSTNode(T->rchild,key); 530 else 531 { 532 if(T->lchild==NULL) 533 { 534 BTREE tmp=T; 535 T=T->rchild; 536 free(tmp); 537 } 538 else if(T->rchild==NULL) 539 { 540 BTREE tmp=T; 541 T=T->lchild; 542 free(tmp) ; 543 } 544 else 545 { 546 //找右子树的最小节点(最左边)的值替换被删节点的值 547 BTREE p=T->rchild; 548 while(p->lchild!=NULL) 549 { 550 p=p->lchild; 551 } 552 T->data=p->data; 553 deleteBSTNode(T->rchild,p->data); 554 555 //也可以找左子树最右的值 556 // BTREE p=T->lchild; 557 // while(p->lchild!=NULL) 558 // { 559 // p=p->lchild; 560 // } 561 // T->data=p->data; 562 // deleteBSTNode(T->lchild,p->data); 563 } 564 } 565 } 566 567 void createBinarySearchTree(BTREE &T,char input[],int n) 568 { 569 int i; 570 for(i=0;i<n;i++) 571 { 572 insertBinarySearchTree_nonrecursive(T,input[i]); 573 // insertBinarySearchTree_recursive(T,input[i]); 574 } 575 576 for(i=0;i<n;i++) 577 {//验证递归查找和非递归查找的正确性 578 if(searchBinarySearchTree_nonrecursive(T,input[i])!=searchBinarySearchTree_recursive(T,input[i])) 579 { 580 printf("error in searchBinarySearchTree\n"); 581 } 582 } 583 } 584 585 586 587 int main() 588 { 589 590 //测试1,特殊序列(表达式 )。度为1的节点空孩子一定要补空,度为0的可以不补;由于表达式内部节点为操作符度都为故不需要补空 591 592 //度为1的节点补空 593 //(*(+A(/(-BC)D))E) 594 //((A+((B-C)/D))*E) 595 //((A((BC-)D/)+)E*) 596 597 //度为1、0的节点补空 598 //( *( +( A##) ( /( -( B##) ( C##) ) ( D##) ) ) ( E##) ) 599 //( ( ( #A#) +( ( ( #B#) -( #C#) ) /( #D#) ) ) *( #E#) ) 600 //(((##A)(((##B)(##C)-)(##D)/)+)(##E)*) 601 602 //测试2,普通序列 603 604 //度为1的节点补空 605 //( A( BD( E( G#H )# ) )( CF# ) ) 606 //( ( DB( ( #GH )E# ) )A( FC# ) ) 607 //( ( D( ( #HG )#E )B )( F#C )A ) 608 609 //度为1、0的节点补空 610 //( A( B( D##) ( E( G#( H##) ) #) ) ( C( F##) #) ) 611 //( ( ( #D#) B( ( #G( #H#) ) E#) ) A( ( #F#) C#) ) 612 //(((##D)((#(##H)G)#E)B)((##F)#C)A) 613 614 615 616 //测试1,特殊序列(表达式 ) ,度为1、0的节点都得补空 617 //*+A##/-B##C##D##E## 618 //#A#+#B#-#C#/#D#*#E# 619 //##A##B##C-##D/+##E* 620 621 //测试2,普通序列 ,度为1、0的节点都得补空 622 //ABD##EG#H###CF### 623 //#D#B#G#H#E#A#F#C# 624 //##D###HG#EB##F#CA 625 626 BTREE T=NULL; 627 628 //加括号:全补空或内补空,前缀、中缀、后缀 629 // char str[]="(*(+A(/(-BC)D))E)"; 630 //char str[]="( *(+(A##)(/(-(B##)(C##))(D##)))(E##) )"; 631 // char str[]="( A( BD( E( G#H )# ) )( CF# ) )"; 632 //char str[]="( A( B( D##) ( E( G#( H##) ) #) ) ( C( F##) #) )"; 633 // createPreOrder_withBrackets(str,T); 634 635 // char str[]="((A+((B-C)/D))*E)"; 636 // char str[]="( ( DB( ( #GH )E# ) )A( FC# ) )"; 637 //char str[]="( ( ( #A#) +( ( ( #B#) -( #C#) ) /( #D#) ) ) *( #E#) )"; 638 // createInOrder_withBrackets(str,T); 639 640 // char str[]="( ( A((BC-)D/)+ )E* )"; 641 //char str[]="(((##A)(((##B)(##C)-)(##D)/)+)(##E)*)"; 642 // char str[]="( ( D( ( #HG )#E )B )( F#C )A )"; 643 // createPostOrder_withBrackets(str,T); 644 645 646 //不加括号:全补空 ,前缀、后缀、广度优先 647 // char str[]="*+A##/-B##C##D##E##"; 648 // char str[]="AB D## E G# H### C F## #"; 649 // createPreOrder(str,T); 650 651 // char str[]="#A#+#B#-#C#/#D#*#E#";//不带括号的中序序列的树是不唯一的,所以没法构建 652 // char str[]="#D#B#G#H#E#A#F#C#"; 653 // createInOrder(str,T); 654 655 // char str[]="##A##B##C-##D/+##E*"; 656 // char str[]="##D # ##H G#EB##F#CA"; 657 // createPostOrder(str,T); 658 659 // char layerSeq[]="12#34#####5"; 660 // createLayerOrder(layerSeq,sizeof(layerSeq)/sizeof(char)-1,T);//广度优先、二叉树形式补空 661 char layerSeq2[]="12#34###5"; 662 createLayerOrder2(layerSeq2,sizeof(layerSeq2)/sizeof(char)-1,T);//广度优先、内补空 。可以将序列转换为完全二叉树形式补空再用上述方法构建,也可以在转换过程中构建。 663 664 //由前序、中序序列 或 后序、中序序列 或 中序、层次序列 构建二叉树。不补空、不加括号。 665 char inorder[]="254163"; 666 char preorder[]="124536"; 667 char postorder[]="542631"; 668 char layerorder[]="123465"; 669 // createByInAndOtherOrder(T,postorder,1,inorder,sizeof(inorder)-1);//法1,三种输入方式都可用此法构建二叉树 670 // createByInAndOtherOrder(T,preorder,0,inorder,sizeof(inorder)-1); 671 // createByInAndOtherOrder(T,layerorder,0,inorder,sizeof(inorder)-1); 672 // createByPreInOrder(T,preorder,0,sizeof(preorder)-1-1,inorder,0,sizeof(inorder)-1-1) ;//法2,知道前序、中序 673 // createByPostInOrder(T,postorder,0,sizeof(postorder)-1-1,inorder,0,sizeof(inorder)-1-1);//法2,知道后序、中序 674 675 //二叉查找树创建、查找(递归、非递归)、删除 676 // char data[]="43265178"; 677 // createBinarySearchTree(T,data,sizeof(data)/sizeof(char)-1); 678 // deleteBSTNode(T,'4'); 679 680 681 682 searchPrefix(T); 683 printf("\n"); 684 searchInfix(T); 685 printf("\n"); 686 searchPostfix(T); 687 printf("\n"); 688 689 return 0; 690 }
遍历
关于树的遍历的一些框架总结可参阅labuldong刷题总结-二叉树系列算法。
"二叉树题目的递归解法可以分两类思路,第一类是遍历一遍二叉树得出答案,第二类是通过分解问题计算出答案,这两类思路分别对应着 回溯算法核心框架 和 动态规划核心框架"。
采用链式存储:深度优先(前序、中序、后序)、广度优先(层次)遍历。(递归、非递归)
采用顺序存储:深度优先(前序、中序、后序)、广度优先(层次)遍历。(递归、非递归),输入为以完全二叉树补空的层次遍历序列,因此遍历方法与采用链式存储的相同,只是改为借助节点编号来反映节点间的父子关系。
总结:

前序遍历的特点:自顶向下、自左向右
后序遍历的特点:自左向右、自底向上
复杂度:
深度优先(DFS):时间复杂度O(n)、空间复杂度O(h)
广度优先(BFS):时间复杂度O(n)、空间复杂度O(n)。
0、二叉树、多叉树、图的BFS算法框架伪代码
见本节尾。
1、链式存储的遍历:(输入的是树的头结点指针)
1)、递归遍历:
前序、中序、后序遍历(大同小异):

1 void searchPrefix(BTREE T) 2 { 3 if(T!=NULL) 4 { 5 printf("%c",T->data); 6 7 searchPrefix(T->lchild); 8 9 searchPrefix(T->rchild); 10 } 11 }
可以加以改进,以打印括号信息或补空信息。

1 void searchPrefix(BTREE T) 2 {//方式1补空:所有的空指针域用特殊字符替代 3 if(T!=NULL) 4 { 5 printf("%c",T->data); 6 7 searchPrefix(T->lchild); 8 9 searchPrefix(T->rchild); 10 } else 11 { 12 printf("#"); 13 } 14 } 15 16 void searchPrefix(BTREE T) 17 {//方式2补空:内部节点的空指针域用特殊字符替代 18 if(T!=NULL) 19 { 20 printf("%c",T->data); 21 22 searchPrefix(T->lchild); 23 if((T->lchild!=NULL || T->rchild!=NULL) && (T->lchild==NULL)){ printf("#"); }//内部节点的空孩子用特殊符号代替 24 25 searchPrefix(T->rchild); 26 if((T->lchild!=NULL || T->rchild!=NULL) && (T->rchild==NULL)){ printf("#"); }//内部节点的空孩子用特殊符号代替 27 } 28 } 29 30 void searchPrefix(BTREE T) 31 {//打印括号 32 if(T!=NULL) 33 { 34 if(T->lchild!=NULL || T->rchild!=NULL){ printf("( "); } 35 printf("%c",T->data); 36 37 searchPrefix(T->lchild); 38 39 searchPrefix(T->rchild); 40 if(T->lchild!=NULL || T->rchild!=NULL){ printf(" )"); } 41 } 42 }
层次遍历:

1 #define M 100 2 void searchLayer(BTREE T) 3 {//广度优先递归遍历,与非递归遍历几乎一样,非递归遍历甚至更方便 4 static BTREE queue[M],p; 5 static int front=-1,rear=-1,isInitial=1; 6 if(T!=NULL) 7 { 8 if(isInitial) 9 { 10 queue[++rear]=T; 11 isInitial=0; 12 } 13 if(front<rear) 14 { 15 p=queue[++front]; 16 printf("%c",p->data); 17 if(p->lchild!=NULL)queue[++rear]=p->lchild; 18 if(p->rchild!=NULL)queue[++rear]=p->rchild; 19 searchLayer(T); 20 } 21 } 22 } 23 24 //也可借助深度遍历来完成,以下是Java版,功能是输出同层的节点 25 /** 26 * Definition for a binary tree node. 27 * public class TreeNode { 28 * int val; 29 * TreeNode left; 30 * TreeNode right; 31 * TreeNode(int x) { val = x; } 32 * } 33 */ 34 public class Solution { 35 public List<List<Integer>> levelOrder(TreeNode root) { 36 List<List<Integer>> res=new ArrayList<>(); 37 if(root==null) 38 { 39 return res; 40 } 41 helper(0,root,res); 42 return res; 43 } 44 public void helper(int depth,TreeNode node,List<List<Integer>>res) 45 {//通过 前序深度优先遍历 来实现 递归版的广度优先遍历 46 if(node==null) return; 47 if(res.size()==depth) 48 { 49 res.add(new ArrayList<Integer>()); 50 } 51 res.get(depth).add(node.val); 52 helper(depth+1,node.left,res); 53 helper(depth+1,node.right,res); 54 } 55 }
2)、非递归遍历:
前序、中序遍历:

1 #define M 100 2 void preOrder(BTREE T) 3 { 4 BTREE stack[M],p=T; 5 int top=-1; 6 if(T!=NULL) 7 { 8 do 9 { 10 while(p!=NULL) 11 { 12 //visit(p); 13 printf("%c",p->data); 14 15 stack[++top]=p; 16 p=p->lchild; 17 } 18 p=stack[top--]; 19 p=p->rchild; 20 }while(!(p==NULL && top==-1)); 21 } 22 } 23 void inOrder(BTREE T) 24 { 25 BTREE stack[M],p=T; 26 int top=-1; 27 if(T!=NULL) 28 { 29 do 30 { 31 while(p!=NULL) 32 { 33 stack[++top]=p; 34 p=p->lchild; 35 } 36 p=stack[top--]; 37 38 //visit(p); 39 printf("%c",p->data); 40 41 42 p=p->rchild; 43 }while(!(p==NULL && top==-1)); 44 } 45 }
后序遍历:(此遍历在访问节点时,栈中保存了根节点到当前节点的父节点的所有节点)

1 void postOrder(BTREE T) 2 {//后序非递归遍历,在访问节点时,栈里保存了根到当前节点的所有节点 3 BTREE stack1[M],p=T; 4 int top=-1,flag,stack2[M];//flag用于标记节点是否能访问 5 if(T!=NULL) 6 { 7 do 8 { 9 while(p!=NULL)//① 10 { 11 stack1[++top]=p; 12 stack2[top]=0; 13 p=p->lchild; 14 } 15 p=stack1[top]; 16 flag=stack2[top--]; 17 if(flag==0) 18 {//不能访问 19 stack1[++top]=p; 20 stack2[top]=1; 21 p=p->rchild; 22 } 23 else 24 {//能访问 25 //visit(p); 26 printf("%c",p->data); 27 28 p=NULL;//为了跳过① 29 } 30 }while(!(p==NULL && top==-1)); 31 } 32 }
层次遍历:

1 void layerOrder(BTREE T) 2 { 3 BTREE queue[M],p; 4 int front=-1,rear=-1; 5 if(T!=NULL) 6 { 7 queue[++rear]=T; 8 9 while(front<rear) 10 { 11 p=queue[++front]; 12 13 //visit(p); 14 printf("%c",p->data); 15 16 if(p->lchild!=NULL) 17 { 18 queue[++rear]=p->lchild; 19 } 20 if(p->rchild!=NULL) 21 { 22 queue[++rear]=p->rchild; 23 } 24 } 25 } 26 }
层次遍历的应用示例:(1)返回一个数组,各元素依次表示各层的节点列表;(2)各元素依次表示各层的节点平均值(LeetCode-637)。两题解法一样只不过处理返回数据的逻辑有异,可借助深度优先或广度优先的层次遍历完成:

public class Solution {//借助深度优先遍历获取每层的节点列表 public List<List<Integer>> levelOrder(TreeNode root) { List<List<Integer>> res=new ArrayList<>(); if(root==null) { return res; } helper(0,root,res); return res; } public void helper(int depth,TreeNode node,List<List<Integer>>res) {//通过 前序深度优先遍历 来实现 递归版的广度优先遍历 if(node==null) return; if(res.size()==depth) { res.add(new ArrayList<Integer>()); } res.get(depth).add(node.val); helper(depth+1,node.left,res); helper(depth+1,node.right,res); } } class Solution {//借助广度优先来获取每层的节点平均值 public List<Double> averageOfLevels(TreeNode root) { List<Double> res=new ArrayList<>(); Queue<TreeNode> queue=new LinkedList<>(); if(null!=root){ queue.add(root); long len,sum; TreeNode curNode; while(queue.size()>0){ len=queue.size(); sum=0; for(int i=0;i<len;i++){ curNode=queue.poll(); sum+=curNode.val; if(curNode.left!=null){queue.add(curNode.left);} if(curNode.right!=null){queue.add(curNode.right);} } res.add(sum*1.0/len); } } return res; } }
2、顺序存储遍历:(输入的是完全二叉树形式的 层次遍历 序列,即除末层外,各层上的空节点都要用特殊字符填充;遍历方式与链式存储的非递归遍历几乎一样,只是这里用数组下标表示父子节点关系,而链式存储中用到是指针)
1)递归遍历:
前序、中序、后序、层次遍历:

1 //bt为输入序列,补空为完全二叉树形式 2 void searchPrefixOfArray(char bt[],int n,int i) 3 { 4 if(i<n && bt[i]!='#') 5 { 6 printf("%c",bt[i]); 7 searchPrefixOfArray(bt,n,2*i+1); 8 searchPrefixOfArray(bt,n,2*i+2); 9 } 10 } 11 void searchInfixOfArray(char bt[],int n,int i) 12 { 13 if(i<n && bt[i]!='#') 14 { 15 searchInfixOfArray(bt,n,2*i+1); 16 printf("%c",bt[i]); 17 searchInfixOfArray(bt,n,2*i+2); 18 } 19 } 20 void searchPostfixOfArray(char bt[],int n,int i) 21 { 22 if(i<n && bt[i]!='#') 23 { 24 searchPostfixOfArray(bt,n,2*i+1); 25 searchPostfixOfArray(bt,n,2*i+2); 26 printf("%c",bt[i]); 27 } 28 } 29 void searchLayerOfArray(char bt[],int n,int i) 30 { 31 while(i<n) 32 { 33 if(bt[i]!='#') 34 { 35 printf("%c",bt[i]); 36 } 37 i++; 38 } 39 }
2)非递归遍历:
前序、中序遍历:

1 void preOrderOfArray(char bt[],int n) 2 {//输入序列按完全二叉树形式补空 3 int stack[M],top=-1,i=0; 4 if(n>0) 5 { 6 do 7 { 8 while(i<n && bt[i]!='#') 9 { 10 //visio(bt[i]); 11 printf("%c",bt[i]); 12 13 stack[++top]=i; 14 i=2*i+1; 15 } 16 i=stack[top--]; 17 i=2*i+2; 18 }while(!((i>=n || bt[i]=='#') && top==-1)); 19 } 20 } 21 22 void inOrderOfArray(char bt[],int n) 23 {//输入序列按完全二叉树形式补空 24 int stack[M],top=-1,i=0; 25 if(n>0) 26 { 27 do 28 { 29 while(i<n && bt[i]!='#') 30 { 31 stack[++top]=i; 32 i=2*i+1; 33 } 34 i=stack[top--]; 35 36 //visio(bt[i]); 37 printf("%c",bt[i]); 38 39 i=2*i+2; 40 }while(!((i>=n || bt[i]=='#') && top==-1)); 41 } 42 }
后序遍历:

1 void postOrderOfArray(char bt[],int n) 2 {//输入序列按完全二叉树形式补空 3 int stack1[M],stack2[M],top=-1,i=0,flag; 4 if(n>0) 5 { 6 do 7 { 8 while(i<n && bt[i]!='#') 9 { 10 stack1[++top]=i; 11 stack2[top]=0; 12 i=2*i+1; 13 } 14 i=stack1[top]; 15 flag=stack2[top--]; 16 17 if(flag==0) 18 { 19 stack1[++top]=i; 20 stack2[top]=1; 21 i=2*i+2; 22 } 23 else 24 { 25 //visit(bt[i]); 26 printf("%c",bt[i]); 27 28 i=n; 29 } 30 }while(!((i>=n || bt[i]=='#') && top==-1)); 31 } 32 }
层次遍历:

1 void layerOrderOfArray(char bt[],int n) 2 {//输入序列按完全二叉树形式补空 3 int queue[M],front=-1,rear=-1,i; 4 if(n>0) 5 { 6 queue[++rear]=0; 7 while(front<rear) 8 { 9 i=queue[++front]; 10 11 //visit(bt[i]); 12 printf("%c",bt[i]); 13 14 if(2*i+1<n && bt[2*i+1]!='#') queue[++rear]=2*i+1; 15 if(2*i+2<n && bt[2*i+2]!='#') queue[++rear]=2*i+2; 16 } 17 } 18 }
附:上述遍历的完整代码:

1 #include<stdio.h> 2 #include<malloc.h> 3 typedef struct node 4 { 5 int data; 6 struct node* lchild; 7 struct node* rchild; 8 }BTNode,*BTREE; 9 10 //链式存储递归遍历(深度优先、广度优先) 11 void searchPrefix(BTREE T) 12 { 13 if(T!=NULL) 14 { 15 printf("%c",T->data); 16 17 searchPrefix(T->lchild); 18 19 searchPrefix(T->rchild); 20 } 21 } 22 void searchInfix(BTREE T) 23 { 24 if(T!=NULL) 25 { 26 searchInfix(T->lchild); 27 28 printf("%c",T->data); 29 30 searchInfix(T->rchild); 31 } 32 } 33 void searchPostfix(BTREE T) 34 { 35 if(T!=NULL) 36 { 37 searchPostfix(T->lchild); 38 39 searchPostfix(T->rchild); 40 41 printf("%c",T->data); 42 } 43 } 44 45 #define M 100 46 void searchLayer(BTREE T) 47 {//广度优先递归遍历,也可借助深度遍历来完成 48 static BTREE queue[M],p; 49 static int front=-1,rear=-1,isInitial=1; 50 if(T!=NULL) 51 { 52 if(isInitial) 53 { 54 queue[++rear]=T; 55 isInitial=0; 56 } 57 if(front<rear) 58 { 59 p=queue[++front]; 60 printf("%c",p->data); 61 if(p->lchild!=NULL)queue[++rear]=p->lchild; 62 if(p->rchild!=NULL)queue[++rear]=p->rchild; 63 searchLayer(T); 64 } 65 } 66 } 67 68 //链式存储非递归遍历(深度优先、广度优先) 69 void preOrder(BTREE T) 70 { 71 BTREE stack[M],p=T; 72 int top=-1; 73 if(T!=NULL) 74 { 75 do 76 { 77 while(p!=NULL) 78 { 79 //visit(p); 80 printf("%c",p->data); 81 82 stack[++top]=p; 83 p=p->lchild; 84 } 85 p=stack[top--]; 86 p=p->rchild; 87 }while(!(p==NULL && top==-1)); 88 } 89 } 90 void inOrder(BTREE T) 91 { 92 BTREE stack[M],p=T; 93 int top=-1; 94 if(T!=NULL) 95 { 96 do 97 { 98 while(p!=NULL) 99 { 100 stack[++top]=p; 101 p=p->lchild; 102 } 103 p=stack[top--]; 104 105 //visit(p); 106 printf("%c",p->data); 107 108 109 p=p->rchild; 110 }while(!(p==NULL && top==-1)); 111 } 112 } 113 void postOrder(BTREE T) 114 {//后序非递归遍历,在访问节点时,栈里保存了根到当前节点父节点的所有节点 115 BTREE stack1[M],p=T; 116 int top=-1,flag,stack2[M];//flag用于标记节点是否能访问 117 if(T!=NULL) 118 { 119 do 120 { 121 while(p!=NULL)//① 122 { 123 stack1[++top]=p; 124 stack2[top]=0; 125 p=p->lchild; 126 } 127 p=stack1[top]; 128 flag=stack2[top--]; 129 if(flag==0) 130 {//不能访问 131 stack1[++top]=p; 132 stack2[top]=1; 133 p=p->rchild; 134 } 135 else 136 {//能访问 137 //visit(p); 138 printf("%c",p->data); 139 140 p=NULL;//为了跳过① 141 } 142 }while(!(p==NULL && top==-1)); 143 } 144 } 145 146 void layerOrder(BTREE T) 147 { 148 BTREE queue[M],p; 149 int front=-1,rear=-1; 150 if(T!=NULL) 151 { 152 queue[++rear]=T; 153 154 while(front<rear) 155 { 156 p=queue[++front]; 157 158 //visit(p); 159 printf("%c",p->data); 160 161 if(p->lchild!=NULL) 162 { 163 queue[++rear]=p->lchild; 164 } 165 if(p->rchild!=NULL) 166 { 167 queue[++rear]=p->rchild; 168 } 169 } 170 } 171 } 172 173 //顺序存储递归遍历(深度优先、广度优先) 174 void searchPrefixOfArray(char bt[],int n,int i) 175 { 176 if(i<n && bt[i]!='#') 177 { 178 printf("%c",bt[i]); 179 searchPrefixOfArray(bt,n,2*i+1); 180 searchPrefixOfArray(bt,n,2*i+2); 181 } 182 } 183 void searchInfixOfArray(char bt[],int n,int i) 184 { 185 if(i<n && bt[i]!='#') 186 { 187 searchInfixOfArray(bt,n,2*i+1); 188 printf("%c",bt[i]); 189 searchInfixOfArray(bt,n,2*i+2); 190 } 191 } 192 void searchPostfixOfArray(char bt[],int n,int i) 193 { 194 if(i<n && bt[i]!='#') 195 { 196 searchPostfixOfArray(bt,n,2*i+1); 197 searchPostfixOfArray(bt,n,2*i+2); 198 printf("%c",bt[i]); 199 } 200 } 201 void searchLayerOfArray(char bt[],int n,int i) 202 { 203 while(i<n) 204 { 205 if(bt[i]!='#') 206 { 207 printf("%c",bt[i]); 208 } 209 i++; 210 } 211 } 212 213 //顺序存储非递归遍历(深度优先、广度优先) 214 void preOrderOfArray(char bt[],int n) 215 {//输入序列按完全二叉树形式补空 216 int stack[M],top=-1,i=0; 217 if(n>0) 218 { 219 do 220 { 221 while(i<n && bt[i]!='#') 222 { 223 //visio(bt[i]); 224 printf("%c",bt[i]); 225 226 stack[++top]=i; 227 i=2*i+1; 228 } 229 i=stack[top--]; 230 i=2*i+2; 231 }while(!((i>=n || bt[i]=='#') && top==-1)); 232 } 233 } 234 235 void inOrderOfArray(char bt[],int n) 236 {//输入序列按完全二叉树形式补空 237 int stack[M],top=-1,i=0; 238 if(n>0) 239 { 240 do 241 { 242 while(i<n && bt[i]!='#') 243 { 244 stack[++top]=i; 245 i=2*i+1; 246 } 247 i=stack[top--]; 248 249 //visio(bt[i]); 250 printf("%c",bt[i]); 251 252 i=2*i+2; 253 }while(!((i>=n || bt[i]=='#') && top==-1)); 254 } 255 } 256 257 void postOrderOfArray(char bt[],int n) 258 {//输入序列按完全二叉树形式补空 259 int stack1[M],stack2[M],top=-1,i=0,flag; 260 if(n>0) 261 { 262 do 263 { 264 while(i<n && bt[i]!='#') 265 { 266 stack1[++top]=i; 267 stack2[top]=0; 268 i=2*i+1; 269 } 270 i=stack1[top]; 271 flag=stack2[top--]; 272 273 if(flag==0) 274 { 275 stack1[++top]=i; 276 stack2[top]=1; 277 i=2*i+2; 278 } 279 else 280 { 281 //visit(bt[i]); 282 printf("%c",bt[i]); 283 284 i=n; 285 } 286 }while(!((i>=n || bt[i]=='#') && top==-1)); 287 } 288 } 289 290 void layerOrderOfArray(char bt[],int n) 291 {//输入序列按完全二叉树形式补空 292 int queue[M],front=-1,rear=-1,i; 293 if(n>0) 294 { 295 queue[++rear]=0; 296 while(front<rear) 297 { 298 i=queue[++front]; 299 300 //visit(bt[i]); 301 printf("%c",bt[i]); 302 303 if(2*i+1<n && bt[2*i+1]!='#') queue[++rear]=2*i+1; 304 if(2*i+2<n && bt[2*i+2]!='#') queue[++rear]=2*i+2; 305 } 306 } 307 } 308 309 310 //构建 311 char nextToken(char str[]) //读取下一字符,略过空格 312 { 313 static int pos=0; 314 while(str[pos]!='\0' && str[pos]==' '){ pos++; } 315 return str[pos++]; 316 } 317 318 319 void createPreOrder(char prefixStr[],BTREE *T) 320 {//输入序列为 全补空、不带括号 的序列 321 char x=nextToken(prefixStr); 322 if(x=='#') 323 { 324 *T=NULL; 325 } 326 else 327 { 328 *T=(BTREE)malloc(sizeof(BTNode)); 329 (*T)->data=x; 330 createPreOrder(prefixStr,&((*T)->lchild)); 331 createPreOrder(prefixStr,&((*T)->rchild)); 332 } 333 } 334 335 int main() 336 { 337 338 //1、链式存储遍历 339 BTREE T=NULL; 340 //char str[]="*+A##/-B##C##D##E##"; 341 char str[]="AB D## E G# H### C F## #"; 342 createPreOrder(str,&T); 343 344 //1.1、链式存储递归遍历 345 printf("链式存储递归遍历:\n"); 346 searchPrefix(T); 347 printf("\n"); 348 349 searchInfix(T); 350 printf("\n"); 351 352 searchPostfix(T); 353 printf("\n"); 354 355 searchLayer(T); 356 printf("\n"); 357 358 //1.2、链式存储非递归遍历 359 printf("\n链式存储非递归遍历:\n"); 360 preOrder(T); 361 printf("\n"); 362 363 inOrder(T); 364 printf("\n"); 365 366 postOrder(T); 367 printf("\n"); 368 369 layerOrder(T); 370 printf("\n"); 371 372 //2、顺序存储遍历 373 char input[]="abcd#f#####e"; 374 int n=sizeof(input)-1; 375 376 //2.1、顺序存储递归遍历 377 printf("\n顺序存储递归遍历:%d\n",n); 378 searchPrefixOfArray(input,n,0); 379 printf("\n"); 380 381 searchInfixOfArray(input,n,0); 382 printf("\n"); 383 384 searchPostfixOfArray(input,n,0); 385 printf("\n"); 386 387 searchLayerOfArray(input,n,0); 388 printf("\n"); 389 390 //2.2、顺序存储非递归遍历 391 printf("\n顺序存储非递归遍历:%d\n",n); 392 preOrderOfArray(input,n); 393 printf("\n"); 394 395 inOrderOfArray(input,n); 396 printf("\n"); 397 398 postOrderOfArray(input,n); 399 printf("\n"); 400 401 layerOrderOfArray(input,n); 402 printf("\n"); 403 404 return 0; 405 }
注:上面的BFS不够通用,实际上二叉树的BFS -> 一般树的BFS -> 图的BFS 本质上是一样的,其算法框架及类比强烈推荐可参阅labuladong-BFS算法框架。通用的算法框架伪代码摘录如下:

//BFS算法框架 // 计算从起点 start 到终点 target 的最近距离 int BFS(Node start, Node target) { Queue<Node> q; // 核心数据结构 Set<Node> visited; // 避免走回头路 q.offer(start); // 将起点加入队列 visited.add(start); int step = 0; // 记录扩散的步数 while (q not empty) { int sz = q.size(); /* 将当前队列中的所有节点向四周扩散 */ for (int i = 0; i < sz; i++) { Node cur = q.poll(); //visited.add(cur);//也可将visit操作放这,另两处就不用了,这样更简洁 /* 划重点:这里判断是否到达终点 */ if (cur is target) return step; /* 将 cur 的相邻节点加入队列 */ for (Node x : cur.adj()) { if (x not in visited) { q.offer(x); visited.add(x); } } } /* 划重点:更新步数在这里 */ step++; } }

//BFS 通过while加深深度、通过for访问同层元素。可借之求解最大深度,最小深度呀,层序遍历结果等问题。 //二叉树、多叉树、图的BFS,原理本质上一样,基于上述BFS框架稍加修改即可 // 二叉树层次遍历:输入一棵二叉树的根节点,层序遍历这棵二叉树 void levelTraverse(TreeNode root) { if (root == null) return 0; Queue<TreeNode> q = new LinkedList<>(); q.offer(root); int depth = 1; // 从上到下遍历二叉树的每一层 while (!q.isEmpty()) { int sz = q.size(); // 从左到右遍历每一层的每个节点 for (int i = 0; i < sz; i++) { TreeNode cur = q.poll(); printf("节点 %s 在第 %s 层", cur, depth); // 将下一层节点放入队列 if (cur.left != null) { q.offer(cur.left); } if (cur.right != null) { q.offer(cur.right); } } depth++; } } // 多叉树的层次遍历:输入一棵多叉树的根节点,层序遍历这棵多叉树 void levelTraverse(TreeNode root) { if (root == null) return; Queue<TreeNode> q = new LinkedList<>(); q.offer(root); int depth = 1; // 从上到下遍历多叉树的每一层 while (!q.isEmpty()) { int sz = q.size(); // 从左到右遍历每一层的每个节点 for (int i = 0; i < sz; i++) { TreeNode cur = q.poll(); printf("节点 %s 在第 %s 层", cur, depth); // 将下一层节点放入队列 for (TreeNode child : cur.children) { q.offer(child); } } depth++; } } // 图的层次遍历:输入起点,进行 BFS 搜索 int BFS(Node start) { Queue<Node> q; // 核心数据结构 Set<Node> visited; // 避免走回头路 q.offer(start); // 将起点加入队列 visited.add(start); int step = 0; // 记录搜索的步数 while (q not empty) { int sz = q.size(); /* 将当前队列中的所有节点向四周扩散一步 */ for (int i = 0; i < sz; i++) { Node cur = q.poll(); //visited.add(cur) //也可以将visit操作放这,另两处就不用了,这样更简洁 printf("从 %s 到 %s 的最短距离是 %s", start, cur, step); /* 将 cur 的相邻节点加入队列 */ for (Node x : cur.adj()) { if (x not in visited) { q.offer(x); visited.add(x); } } } step++; } }
二叉树、多叉树、图的BFS,原理本质上一样,通过while加深深度、通过for访问同层元素。可借之求解最大深度,最小深度,层序遍历结果等问题。算法中的for循环用于知道元素在第几层,若题目无该需求则也可不要该循环从而更简洁。
前序位置的代码只能从函数参数中获取父节点传递来的数据,而后序位置的代码不仅可以获取参数数据、还可以获取到子树通过函数返回值传递回来的数据。故一旦你发现题目和子树有关,那大概率要给函数设置合理的定义和返回值,在后序位置写代码了。
写树相关的算法,简单说就是,先搞清楚对当前 root 节点「该做什么」(涉及到函数返回值的含义定义)以及「什么时候做」(在前中后序三者的哪个位置做),然后根据函数定义递归调用子节点,递归调用会让孩子节点做相同的事情。
递归算法的关键要明确函数的定义,相信这个定义,而不要跳进递归细节。
销毁
通过遍历来销毁:后序递归遍历;后序非递归遍历(此时栈中保存了当前节点的双亲节点到根节点的所有节点)
特殊二叉树
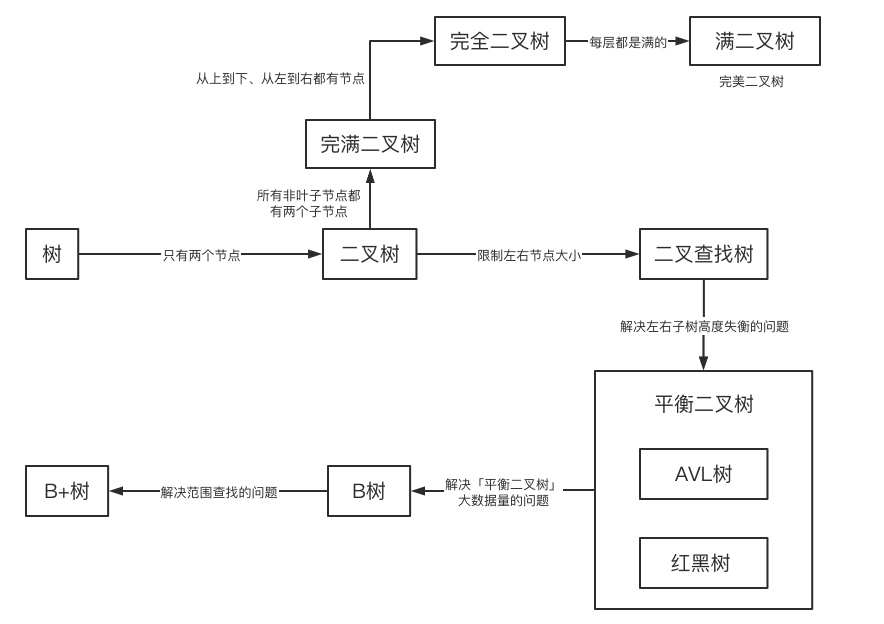
1、理想平衡二叉树(只有最后一层可能不满)
满二叉树(是理想平衡二叉树,且各层都满)
完全二叉树(是理想平衡二叉树,且最后一层节点依次从左填到右)
2、正则(正规)二叉树:只有度为0或2的节点的二叉树
3、线索二叉树:将二叉树的空指针域用来存储直接前驱、直接后继节点(称为线索)的二叉树,这样遍历就不需要用栈了。
通过遍历二叉树进行二叉树的线索化,根据遍历方法的不同分为前序线索二叉树、中序线索二叉树、后序线索二叉树。
前序线索二叉树中不能找到某些节点的直接前驱节点、后序线索二叉树不能找到某些节点的直接后继节点,因此通常用中序线索二叉树。
4、哈夫曼树(最优二叉树):带权路径长度WPL最小的二叉树。
WPL=Σ(叶节点权值×路径长度)= 非根节点的权值和 = 非叶节点的权值和
根节点权值 与 叶节点权值和 相等
没有度为1的节点(即哈夫曼树是正则二叉树)、给定权值序列构造的哈夫曼树不唯一但WPL相同。
5、二叉查找树(亦称二叉排序树、二叉搜索树)BST:每个节点的左子树的所有节点的值小于该节点值,右子树的所有节点值小于该节点值的二叉树。
查找长度:
内部节点、外部节点、平均查找长度ASL(成功时ASL1、失败时ASL2、综合)、内路径长度IPL、外路径长度EPL。EPL=IPL+2n,
某个节点查找成功时比较次数=所在层数=路径+1,故所有节点查找成功的比较次数=IPL+n;某个值查找失败的比较次数=最后一次比较的叶节点的层=外部节点的外路径长度,故所有节点查找失败的比较次数为EPL
ASL1=(IPL+n)/n,ASL2=EPL/(n+1)
ASL=(IPL+n+EPL)/(n+n+1)=(3n+IPL)/(2n+1),当IPL最小时平均查找长度最小。
种数:对包含n个数的有序序列,其BST树有卡特兰数种。
二叉查找树的中序遍历得到升序序列,判断二叉树是否是二叉查找树可以看中序遍历序列是否升序来判定(递归、非递归均可),当然,还有其他更好的方法。
1)二叉查找树创建(递归、非递归):(只给定BST的前序序列即可构建出BST,依次从前往后插入每个元素即可;只给定后序序列时类似,只不过是从后完全插入)

1 void insertBinarySearchTree_nonrecursive(BTREE &T,char item) 2 { 3 BTREE p,q; 4 p=(BTREE)malloc(sizeof(BTNode)); 5 p->data=item; 6 p->lchild=NULL; 7 p->rchild=NULL; 8 if(T==NULL) T=p; 9 else 10 { 11 q=T; 12 while(1) 13 { 14 if(item < q->data) 15 { 16 if(q->lchild!=NULL) q=q->lchild; 17 else 18 { 19 q->lchild=p; 20 break; 21 } 22 } 23 else 24 { 25 if(q->rchild!=NULL) q=q->rchild; 26 else 27 { 28 q->rchild=p; 29 break; 30 } 31 } 32 } 33 } 34 } 35 void insertBinarySearchTree_recursive(BTREE &T,char item) 36 { 37 if(T==NULL) 38 { 39 T=(BTREE)malloc(sizeof(BTNode)); 40 T->data=item; 41 T->lchild=NULL; 42 T->rchild=NULL; 43 } 44 else if(item< T->data) 45 { 46 insertBinarySearchTree_recursive(T->lchild,item); 47 } 48 else 49 { 50 insertBinarySearchTree_recursive(T->rchild,item); 51 } 52 } 53 void createBinarySearchTree(BTREE &T,char input[],int n) 54 { 55 int i; 56 for(i=0;i<n;i++) 57 { 58 // insertBinarySearchTree_nonrecursive(T,input[i]); 59 insertBinarySearchTree_recursive(T,input[i]); 60 } 61 }
2)二叉查找树查找节点(递归、非递归):

1 BTREE searchBinarySearchTree_nonrecursive(BTREE T,char item) 2 { 3 BTREE p=T; 4 while(p!=NULL) 5 { 6 if(p->data==item) 7 return p; 8 else if(p->data<item) 9 p=p->lchild; 10 else 11 p=p->rchild; 12 } 13 return p; 14 } 15 16 BTREE searchBinarySearchTree_recursive(BTREE T,char item) 17 { 18 if(T==NULL || T->data==item) 19 return T; 20 else if(T->data < item) 21 searchBinarySearchTree_recursive(T->lchild,item); 22 else 23 searchBinarySearchTree_recursive(T->rchild,item); 24 }
3)二叉查找树删除节点(删除后维护BST的性质,BST形状可能不唯一):相关:LeetCode450
先找到节点,若找到,则进行删除操作:
a、若是叶子节点则直接删除;
b、否则,若左孩子空、右孩子非空,则删掉后用右孩子代替之;
c、否则,若左孩子非空、右孩子空,则删掉后用左孩子替代之;
d、否则,值用右子树的最小节点(即右子树的最左节点)的值代替之,并维护右子树即:对该最左节点进行a或b操作。当然,也可以用左子树的最大节点(即左子树的最右节点)的值代替之并对该最右节点进行a或c操作。
递归法:

1 void deleteBSTNode(BTREE &T,char key) 2 {//删除二叉查找树中的一个节点。也可以借助后序非递归遍历来实现 ,此时栈顶元素存在的话为当前节点的父节点 3 if(T==NULL)return; 4 else if(key<T->data)deleteBSTNode(T->lchild,key); 5 else if(key>T->data)deleteBSTNode(T->rchild,key); 6 else 7 { 8 if(T->lchild==NULL) 9 { 10 BTREE tmp=T; 11 T=T->rchild; 12 free(tmp); 13 } 14 else if(T->rchild==NULL) 15 { 16 BTREE tmp=T; 17 T=T->lchild; 18 free(tmp) ; 19 } 20 else 21 { 22 //找右子树的最小节点(最左边)的值替换被删节点的值 23 BTREE p=T->rchild; 24 while(p->lchild!=NULL) 25 { 26 p=p->lchild; 27 } 28 T->data=p->data; 29 deleteBSTNode(T->rchild,p->data); 30 31 //也可以找左子树最右的值 32 // BTREE p=T->lchild; 33 // while(p->rchild!=NULL) 34 // { 35 // p=p->rchild; 36 // } 37 // T->data=p->data; 38 // deleteBSTNode(T->lchild,p->data); 39 } 40 } 41 }
非递归法:(用后序非递归遍历,比较麻烦)
4)验证是否是二叉查找树:二叉查找树的中序遍历得到升序序列,判断二叉树是否是二叉查找树可以看中序遍历序列是否升序来判定(递归、非递归均可),当然,还有其他更好的方法,查看相关--LeetCode98。

1 /** 2 * Definition for a binary tree node. 3 * public class TreeNode { 4 * int val; 5 * TreeNode left; 6 * TreeNode right; 7 * TreeNode(int x) { val = x; } 8 * } 9 */ 10 public class Solution {//通过中序遍历。是BST 等价于 中序遍历序列是升序 11 public boolean isValidBST(TreeNode root) { 12 inOrder(root); 13 return isValid; 14 } 15 private TreeNode lastVisited=null; 16 private boolean isValid=true; 17 private void inOrder(TreeNode root) 18 {//中序遍历,如果遇到上次访问节点值比当前根节点大,则invalid并结束 19 if(root!=null) 20 { 21 inOrder(root.left); 22 23 if(lastVisited!=null) 24 { 25 if(lastVisited.val>=root.val) 26 { 27 isValid=false; 28 } 29 } 30 lastVisited=root; 31 32 inOrder(root.right); 33 } 34 } 35 } 36 37 public class Solution { 38 public boolean isValidBST(TreeNode root) { 39 return isBST(root, Long.MIN_VALUE, Long.MAX_VALUE); 40 } 41 42 private boolean isBST(TreeNode root, long min, long max) {//通过前序遍历 43 44 if(root == null) { 45 return true; 46 } 47 48 // check the node's restriction 49 if(!(root.val > min && root.val < max)) { 50 return false; 51 } 52 53 // check left 54 boolean l = isBST(root.left, min, root.val); 55 boolean r = isBST(root.right, root.val, max); 56 57 return (l == true && r == true); 58 } 59 }
最优二叉查找树:给定一个有序序列{xi},i∈[1,n],再给定查找每个序列值的概率bi以及查找值不存在时落入区间(xi, xi+1),i∈[0,n]的概率ai,所有的ai、bi总和为1。如何构建二叉搜索树使平均查找路径最短?——动态规划(与求矩阵连乘的最少乘法次数很像)
二叉查找树的平衡:普通的二叉查找树虽然平均时间复杂度为O(lgn),但最坏情况下退化为线性链表此时时间复杂度为O(n),因此实际应用中不实用。通常考虑平衡性,如:
5.1、平衡二叉树(亦称平衡二叉查找树、AVL树):每个节点的左右子树深度最多差1的二叉查找树
注意,平衡二叉树最早是为了改进二叉排序树的性能而考虑平衡性进而提出来的——即AVL树(当然,其平衡性没有理想平衡二叉树要求那么严,否则维护成本太高),所以一般说到平衡二叉树指的是平衡的二叉排序树。
最小平衡二叉树:节点数最少时的平衡二叉树,此时每个分支节点的左右子树深度都恰好相差1。设高为h的最小平衡二叉树的节点总数为F(h),则F(h)=左子树节点总数+右子树节点总数+1,即F(h)=F(h-1)+F(h-2)+1,F(1)=1、F(2)=2。
5.2、红黑树:是另一种考虑了平衡性了的二叉查找树(平衡性比平衡二叉树弱以减少增删节点时所需的维护平衡性的开销)。(可参阅: 红黑树原理和算法、红黑树讲解)
性质:
1、每个节点为红色或黑色;
2、根节点为黑色;
3、叶节点为黑色(此叶节点指为空NULL的叶节点);
4、红色节点的子节点一定是黑色;
5、一个节点到它每个同层子孙节点的路径上黑色节点数相同(此条保证了没有一条路径会比其他路径长2倍,故红黑树是相对平衡的BST)。
含有n个节点的红黑树高度最多为 2*ceil( log2(n+1) ),即高为h的红黑树其节点数至少有2h/2-1个,因此最坏时间复杂度为O(lgn)。
复杂度:插入、删除、查找的平均和最坏时间复杂度为O(lgn),效率高。插入、删除节点可能会破坏上述性质,因此需要进行左旋或右旋转操作以维护性质。由于红黑树平衡性要求没有平衡二叉树那么高,因此插入或删除节点的维护代价比后者低。
应用:主要用来存储有序数据,如Java中的TreeMap、TreeSet,C++中STL中的map、set,Linux中的内存管理等就用了红黑树实现。
5.3、B、B+树:它们不是二叉树查找树,但由二叉查找树扩展而来,是多叉平衡查找树。详情可参阅:https://segmentfault.com/a/1190000020416577
二叉搜索树效率高,但数据很多时树高会很大从而导致IO太多(一层一次IO)。为了减少IO(即减少树高),可增加节点中关键字数量变成多叉树,就产生了B、B+树。
m阶B树特点:
数量关系:节点的子节点最多m个;非根内部节点中的关键字个数∈[m/2, m-1](根节点的则∈[1, m-1])。
关键字关系:节点内关键字按升序排列,各关键字的左子树的所有关键字都小于该关键字、右子树的所有关键字都大于该关键字。
存储内容:所有节点中都存索引、与索引对应的数据。
生成方式:所有叶子节点在同一层,树是自底向上构建的(这点与二叉搜索树不同),在插入(删除)关键字后若不满足数量关系则需进行节点分裂(合并)。
m阶B+树的特点:与B树很像,不同之处在于:
关键字关系:各关键字右子树的所有关键字大于等于该关键字,而不是B树的大于。故该关键字与右子树第一个关键字值一样。
存储内容:内部节点相当于路标只存索引不存数据,所有数据存储在叶子节点。故同样大小的节点,B+树比B树可存更多的关键字,从而存储效率更高;且查询时需要访问的节点数是固定的,而B树不是,故前者更稳定。
范围访问:叶子节点间从小到大有序排列且用双向链表连接,形成双向有序链表,故B+树除了B树的 random access 外还支持范围访问。
故B+树相比于B树优势有三:IO更少、访问更稳定、范围访问。
注:IO中节点大小通常固定为PageCace页大小4KB,这样访问一个节点仅需要一次IO。故索引列数据类型应该尽可能小,这样m就可以越大,进而树高就越小,从而IO次数更少。MySQL InnoDB存储引擎中通常树高不超过3。
笔者基于内存的B+树实现:

1 package buaa.act.ucar.imtg.index.node.temporal; 2 3 import java.util.ArrayList; 4 import java.util.List; 5 6 import buaa.act.ucar.util.config.ConfigFileParser; 7 8 /** 9 * The implementation of B+-Tree based on the implementation in reference <a>http://en.wikipedia.org/wiki/B%2B_tree</a><br> 10 * <br> 11 * 一个节点的某个key>左孩子节点内所有的key且≤右孩子节点内所有的key。等号只有对于叶节点的父节点成立,也即B+tree的内部节点的key都不同。 <br> 12 * <br> 13 * 若插入后节点的键的数量超出上阈值1时即进行分裂,一个节点分裂成两个后,对于叶节点来说后节点的第一个元素的键作为新键复制到父节点、对于内部节点来说后节点的第一个元素的键移到父节点。<br> 14 * 删除时若有节点合并则合并过程与上述过程相反。<br> 15 * <br> 16 * <br> 17 * note: 启用插入借位(或称旋转)能减少内存占用。然而:<br> 18 * 对于随机写入来说,不采用插入借位会提高查询性能,因为每个节点的数据量少了,能减少比较;<br> 19 * 对于升序插入来说,启用插入借位总是能提高插入、查询、删除性能,对于升序输入来说,采用size-1:1的分裂方法能进一步提高性能。 20 * 21 * 22 * @author zsm 23 * 24 * @param <K> 25 * @param <V> 26 */ 27 public class BPlusTree<K extends Comparable<K>, V> { 28 29 /** 30 * 树的分支<br> 31 * a) 非根内部节点的孩子数: [ Math.ceil(factor/2), factor ]<br/> 32 * b) 叶子节点的孩子数: [ Math.ceil(factor/2)-1, factor-1 ] 33 */ 34 private int factor; 35 36 private static final int DEFAULT_FACTOR = 5; 37 38 private int MIN_CHILDREN_FOR_INTERNAL; 39 private int MAX_CHILDREN_FOR_INTERNAL; 40 private int MIN_CHILDREN_FOR_LEAF; 41 private int MAX_CHILDREN_FOR_LEAF; 42 43 // 给插入时用 44 private Object[] tmpNewKeys; 45 private Node[] tmpNewPointers; 46 private Object[] tmpNewValues; 47 48 private Node<K, V> root; 49 50 /** 叶节点数据记录总数 */ 51 private int dataCount; 52 53 /** 54 * 待存数据是否有序存入 ,决定了节点的分裂方案:<br> 55 * ASCENDING:分裂后新节点存一个元素 <br> 56 * DESCENDING:分裂后原节点存一个元素<br> 57 * RANDOM:对半分 58 */ 59 public enum InputDataOrder { 60 ASCENDING, DESCENDING, RANDOM 61 } 62 63 private InputDataOrder inputDataOrder; 64 65 public BPlusTree(InputDataOrder inputDataOrder) { 66 this(DEFAULT_FACTOR, inputDataOrder); 67 } 68 69 public BPlusTree(int factor, InputDataOrder inputDataOrder) { 70 if (factor < 3) { 71 System.out.print("order must be greater than 2"); 72 System.exit(0); 73 } 74 75 // System.out.println("factor for tree:" + factor); 76 this.inputDataOrder = inputDataOrder; 77 78 this.factor = factor; 79 80 this.MIN_CHILDREN_FOR_INTERNAL = (this.factor + 1) / 2; 81 this.MAX_CHILDREN_FOR_INTERNAL = this.factor; 82 this.MIN_CHILDREN_FOR_LEAF = this.MIN_CHILDREN_FOR_INTERNAL - 1; 83 this.MAX_CHILDREN_FOR_LEAF = this.MAX_CHILDREN_FOR_INTERNAL - 1; 84 85 // 比允许的最大值多1 86 tmpNewKeys = new Object[MAX_CHILDREN_FOR_INTERNAL]; 87 tmpNewPointers = new Node[MAX_CHILDREN_FOR_INTERNAL + 1]; 88 tmpNewValues = new Object[MAX_CHILDREN_FOR_LEAF + 1]; 89 90 this.root = new LeafNode<K, V>(); 91 this.dataCount = 0; 92 } 93 94 /** 95 * 根据给定的key获取对应的值 96 */ 97 public V get(K key) { 98 return this.root.get(key); 99 } 100 101 /** 102 * 获取指定key范围内的值 103 */ 104 public ArrayList<V> get(K keyStart, K keyEnd) { 105 if (keyStart.compareTo(keyEnd) > 0) { 106 return null; 107 } 108 LeafNode<K, V> leafNodeStart, leafNodeEnd; 109 if (root instanceof LeafNode) {// 说明整个树只有一个节点 110 leafNodeStart = leafNodeEnd = (LeafNode<K, V>) root; 111 } else { 112 leafNodeStart = ((InternalNode<K, V>) root).getLeafNodeByKey(keyStart); 113 leafNodeEnd = ((InternalNode<K, V>) root).getLeafNodeByKey(keyEnd); 114 } 115 116 // 获取结果 117 ArrayList<V> res = new ArrayList<>(); 118 int nodeSize; 119 K tmpK; 120 do { 121 nodeSize = leafNodeStart.size; 122 for (int i = 0; i < nodeSize; i++) { 123 tmpK = (K) leafNodeStart.keys[i]; 124 if (keyStart.compareTo(tmpK) <= 0 && tmpK.compareTo(keyEnd) <= 0) { 125 res.add((V) leafNodeStart.values[i]); 126 } 127 } 128 leafNodeStart = (LeafNode<K, V>) leafNodeStart.next; 129 } while (leafNodeStart != leafNodeEnd.next); 130 return res; 131 } 132 133 /** 134 * 获取指定oid在指定key范围内的值,此方法在B+tree key 为gpstime#oid组合的String类型时 才适用 135 */ 136 public ArrayList<V> get(String oid, K keyStart, K keyEnd) { 137 if (keyStart.compareTo(keyEnd) > 0) { 138 return null; 139 } 140 LeafNode<K, V> leafNodeStart, leafNodeEnd; 141 if (root instanceof LeafNode) {// 说明整个树只有一个节点 142 leafNodeStart = leafNodeEnd = (LeafNode<K, V>) root; 143 } else { 144 leafNodeStart = ((InternalNode<K, V>) root).getLeafNodeByKey(keyStart); 145 leafNodeEnd = ((InternalNode<K, V>) root).getLeafNodeByKey(keyEnd); 146 } 147 148 // 获取结果 149 ArrayList<V> res = new ArrayList<>(); 150 int nodeSize; 151 K tmpK; 152 String tmpOid; 153 do { 154 nodeSize = leafNodeStart.size; 155 for (int i = 0; i < nodeSize; i++) { 156 tmpK = (K) leafNodeStart.keys[i]; 157 tmpOid = tmpK.toString(); 158 // System.out.println("_" + tmpOid); 159 tmpOid = tmpOid.substring(tmpOid.indexOf(ConfigFileParser.bplustree_TagForDivdingGpstimeDevsn) + 1);// 获取oid 160 if (tmpOid.equals(oid) && keyStart.compareTo(tmpK) <= 0 && tmpK.compareTo(keyEnd) <= 0) { 161 res.add((V) leafNodeStart.values[i]); 162 } 163 } 164 leafNodeStart = (LeafNode<K, V>) leafNodeStart.next; 165 } while (leafNodeStart != leafNodeEnd.next); 166 return res; 167 } 168 169 /** 170 * 插入键值对,若键已存在,则更新值 171 */ 172 public void set(K key, V value) { 173 if (key == null) 174 throw new NullPointerException("key must not be null."); 175 176 Node<K, V> node = this.root.insert(key, value); 177 if (node != null) 178 this.root = node; 179 } 180 181 /** 182 * 删除给定的key对应的值 183 */ 184 public void remove(K key) { 185 // TODO Auto-generated method stub 186 Node node = this.root.remove(key); 187 if (node != null) { 188 this.root = node; 189 } 190 } 191 192 /** 获取树的根节点 */ 193 public Node<K, V> getRoot() { 194 return this.root; 195 } 196 197 /** 获取最左边的叶节点 */ 198 public LeafNode<K, V> getLeftestLeafNode() { 199 Node<K, V> node = this.root; 200 while (!(node instanceof LeafNode)) { 201 node = ((InternalNode<K, V>) node).pointers[0]; 202 } 203 return (LeafNode<K, V>) node; 204 } 205 206 /** 获取树中数据记录总数 */ 207 public int getDataCount() { 208 return this.dataCount; 209 } 210 211 /** 212 * 获取所有value 213 */ 214 public List<V> getAllValues() { 215 List<V> res = new ArrayList<>(this.dataCount); 216 LeafNode<K, V> leafNode = getLeftestLeafNode(); 217 while (leafNode != null) { 218 for (int i = 0; i < leafNode.size; i++) { 219 res.add((V) leafNode.values[i]); 220 } 221 leafNode = (LeafNode<K, V>) leafNode.next; 222 } 223 return res; 224 } 225 226 /** 获取树的高度,最少为1 */ 227 public int getHeight() { 228 int height = 1; 229 Node<K, V> node = this.root; 230 while (!(node instanceof LeafNode)) { 231 node = ((InternalNode<K, V>) node).pointers[0]; 232 height++; 233 } 234 return height; 235 } 236 237 /** 打印树结构 */ 238 public void printTree() { 239 this.printTreeFrom(this.root); 240 } 241 242 private void printTreeFrom(Node<K, V> startRoot) { 243 System.out.println("print tree:"); 244 Node<K, V> curNode = null; 245 do { 246 curNode = startRoot; 247 while (curNode != null) { 248 // System.out.print("|"); 249 // for (int i = 0; i < curNode.size; i++) { 250 // System.out.print(curNode.keys[i]); 251 // if (i != curNode.size - 1) { 252 // System.out.print(","); 253 // } 254 // } 255 // System.out.print("| "); 256 System.out.print(curNode); 257 curNode = curNode.next; 258 } 259 if (startRoot instanceof InternalNode) { 260 startRoot = ((InternalNode) startRoot).pointers[0]; 261 } else { 262 startRoot = null; 263 } 264 System.out.println(); 265 } while (startRoot != null); 266 } 267 268 /** 269 * the abstract node definition, define the operation of leaf node and internal node. 270 * 271 * @param <K> 272 * @param <V> 273 */ 274 abstract class Node<K extends Comparable<K>, V> { 275 276 protected Node<K, V> parent; 277 278 protected Node<K, V> previous, next; 279 280 protected Object[] keys; 281 282 /** 283 * 节点中key的个数 284 */ 285 protected int size; 286 287 protected abstract V get(K key); 288 289 /** 290 * if new parent node is created when insert the key-value, the created parent node is returned, otherwise, this method return null.<br> 291 * 若已存在该key则更新值,结束。<br> 292 * 否则找到应该插入的位置。若插入后不会使得当前节点空间上溢则结束;若会上溢则依次看左右相邻<b>兄弟节点</b>是否有空间,有则移一个元素到该兄弟节点并进行必要调整(此操作也称旋转或借位);否则当前节点分裂。内部节点的借位和分裂操作与叶子节点的操作不太一样。 293 * 294 * @param key 295 * @param value 296 * @return 297 */ 298 protected abstract Node<K, V> insert(K key, V value); 299 300 /** 301 * if root is removed, the new root is returned, otherwise, this method return null.<br> 302 * 先删除,然后判断:<br> 303 * 若当前节点是根节点则结束;否则若当前节点的空间未下溢则结束;否则依次看左右相邻<b>兄弟节点</b>是否元素个数大于最小值,若是则借一个元素到当前节点(称旋转或借位),否则依次看与左兄弟节点还是右兄弟节点合并。内部节点的借位和合并操作与叶子节点的操作不太一样。 <br> 304 * 可以改进:节点合并时存起该丢弃的节点,在节点分裂时不用new新节点而是复用该节点,以节省空间。 305 * 306 * @param key 307 * @param value 308 * @return 309 */ 310 protected abstract Node<K, V> remove(K key); 311 312 @Override 313 public String toString() { 314 StringBuilder nodeKeyInfo = new StringBuilder(); 315 nodeKeyInfo.append("|"); 316 for (int i = 0; i < this.size; i++) { 317 nodeKeyInfo.append(this.keys[i]); 318 if (i != this.size - 1) { 319 nodeKeyInfo.append(","); 320 } 321 } 322 nodeKeyInfo.append("| "); 323 return nodeKeyInfo.toString(); 324 } 325 } 326 327 /** 328 * the internal node which manages the pointers. 329 * 330 * @param <K> 331 * @param <V> 332 */ 333 final class InternalNode<K extends Comparable<K>, V> extends Node<K, V> { 334 private Node<K, V>[] pointers; 335 336 public InternalNode() { 337 this.size = 0; 338 this.pointers = new Node[MAX_CHILDREN_FOR_INTERNAL]; 339 this.keys = new Object[MAX_CHILDREN_FOR_INTERNAL - 1]; 340 this.parent = null; 341 342 this.previous = null; 343 this.next = null; 344 } 345 346 @Override 347 protected V get(K key) { 348 // int i = 0; 349 // for (; i < this.size; i++) { 350 // if (key.compareTo((K) this.keys[i]) < 0) 351 // break; 352 // } 353 // return this.pointers[i].get(key); 354 LeafNode<K, V> tmpNode = getLeafNodeByKey(key); 355 if (tmpNode == null) { 356 return null; 357 } else { 358 return tmpNode.get(key); 359 } 360 } 361 362 @Override 363 protected Node<K, V> insert(K key, V value) { 364 // int i = 0; 365 // for (; i < this.size; i++) { 366 // if (key.compareTo((K) this.keys[i]) < 0) 367 // break; 368 // } 369 // return this.pointers[i].insert(key, value); 370 LeafNode<K, V> tmpNode = getLeafNodeByKey(key); 371 if (tmpNode == null) { 372 return null; 373 } else { 374 return tmpNode.insert(key, value); 375 } 376 } 377 378 @Override 379 protected Node<K, V> remove(K key) { 380 // TODO Auto-generated method stub 381 LeafNode<K, V> tmpNode = getLeafNodeByKey(key); 382 if (tmpNode == null) { 383 return null; 384 } else { 385 return tmpNode.remove(key); 386 } 387 } 388 389 /** 390 * 根据给定的key获取应在的LeafNode,即使该LeafNode没有该key 391 */ 392 public LeafNode<K, V> getLeafNodeByKey(K key) { 393 Node<K, V> tmpNode = this; 394 int i; 395 do { 396 for (i = 0; i < tmpNode.size; i++) { 397 if (key.compareTo((K) tmpNode.keys[i]) < 0) 398 break; 399 } 400 tmpNode = ((InternalNode<K, V>) tmpNode).pointers[i]; 401 } while (tmpNode instanceof InternalNode); 402 return (LeafNode<K, V>) tmpNode; 403 } 404 405 /** 406 * 在当前节点中插入指定的key及其相应左右孩子树。设key应当在当前节点的关键字a、b间,leftChild、rightChild中的任意一个关键字分别为x、y,则有a≤x<key≤y<b 407 * 408 * @return 若树高度增加导致产生新根节点则返回该新根节点,否则返回null 409 */ 410 private Node<K, V> insert(K key, Node<K, V> leftChild, Node<K, V> rightChild) { 411 if (this.size == 0) {// 增加一层 412 // System.out.println("**internal insert " + key + " in 0 of " + this.toString()); 413 this.size++; 414 this.pointers[0] = leftChild; 415 this.pointers[1] = rightChild; 416 this.keys[0] = key; 417 return this; 418 } 419 420 // key应该在的位置 421 int i; 422 for (i = 0; i < this.size; i++) { 423 if (key.compareTo((K) this.keys[i]) < 0) { 424 break; 425 } 426 } 427 // System.out.println("**internal insert " + key + " in " + i + " of " + this.toString()); 428 429 // 未满,直接插入 430 if (this.size + 1 < MAX_CHILDREN_FOR_INTERNAL) { 431 for (int j = this.size; j > i; j--) { 432 this.keys[j] = this.keys[j - 1]; 433 this.pointers[j + 1] = this.pointers[j]; 434 } 435 this.keys[i] = key; 436 this.pointers[i + 1] = rightChild; 437 this.size++; 438 return null; 439 } 440 // 以下分支:插入后会满 441 // 442 else if (this.previous != null && (this.previous.parent == this.parent) 443 && this.previous.size < MAX_CHILDREN_FOR_LEAF) {// 旋转操作:放一个到前一兄弟节点 444 // 找到父节点中分界key的位置 445 Node<K, V> parent = this.parent; 446 K tmpKey = (K) this.keys[0]; 447 int j; 448 for (j = parent.size - 1; j >= 0; j--) { 449 if (tmpKey.compareTo((K) (parent.keys[j])) >= 0) {// 若维护叶节点第一个key等于父节点分界key,则只会= 450 break; 451 } 452 } 453 454 // 把当前节点的一个元素放到目标兄弟节点后在当前节点插入key-value,并更新父节点key 455 InternalNode<K, V> toNode = (InternalNode<K, V>) this.previous; 456 457 // 移动一个节点到前一节点 458 toNode.keys[toNode.size] = parent.keys[j]; 459 toNode.pointers[toNode.size + 1] = this.pointers[0]; 460 this.pointers[0].parent = toNode; 461 toNode.size++; 462 463 // 更新父节点key并在当前节点插入新元素 464 if (i == 0) {// 按理应插入到当前节点首位 465 // 更新父节点key 466 parent.keys[j] = key; 467 // 当前节点插入新元素 468 this.pointers[0] = rightChild; 469 } else { 470 // 更新父节点key 471 parent.keys[j] = this.keys[0]; 472 // 当前节点插入新元素.移掉一个元素到目的节点后,待插元素应放在i-1的位置 473 this.pointers[0] = this.pointers[1]; 474 int insertPos = i - 1; 475 for (int k = 0; k < insertPos; k++) { 476 this.keys[k] = this.keys[k + 1]; 477 this.pointers[k + 1] = this.pointers[k + 2]; 478 } 479 this.keys[insertPos] = key; 480 this.pointers[insertPos + 1] = rightChild; 481 } 482 483 return null; 484 485 } else if (this.next != null && (this.next.parent == this.parent) 486 && this.next.size < MAX_CHILDREN_FOR_LEAF) {// 旋转操作: 放一个到下一兄弟节点 487 488 InternalNode<K, V> toNode = (InternalNode<K, V>) this.next; 489 // 找到父节点中分界key的位置 490 Node<K, V> parent = this.parent; 491 K tmpKey = (K) toNode.keys[0]; 492 int j; 493 for (j = parent.size - 1; j >= 0; j--) { 494 if (tmpKey.compareTo((K) (parent.keys[j])) >= 0) {// 若维护叶节点第一个key等于父节点分界key,则只会= 495 break; 496 } 497 } 498 499 // 腾出首位 500 for (int k = toNode.size; k > 0; k--) { 501 toNode.keys[k] = toNode.keys[k - 1]; 502 toNode.pointers[k + 1] = toNode.pointers[k]; 503 } 504 toNode.pointers[1] = toNode.pointers[0]; 505 toNode.size++; 506 507 // 把当前节点的一个元素放到目标兄弟节点后在当前节点插入key-value,并更新父节点key 508 if (i == this.size) { 509 toNode.keys[0] = parent.keys[j]; 510 toNode.pointers[0] = rightChild; 511 rightChild.parent = toNode; 512 513 parent.keys[j] = key; 514 } else { 515 toNode.keys[0] = parent.keys[j]; 516 toNode.pointers[0] = this.pointers[this.size]; 517 toNode.pointers[0].parent = toNode; 518 519 parent.keys[j] = this.keys[this.size - 1]; 520 521 for (int k = this.size - 1; k > i; k--) { 522 this.keys[k] = this.keys[k - 1]; 523 this.pointers[k + 1] = this.pointers[k]; 524 } 525 this.keys[i] = key; 526 this.pointers[i + 1] = rightChild; 527 } 528 529 return null; 530 531 } else {// 分裂 532 // 已满,需要分裂 533 { 534 // InternalNode<K, V> newNode = new InternalNode<K, V>(); 535 // 536 // int tmpSizeIfInserted = this.size + 1; 537 // // 如果插入后需要被提到父节点的key及其下标,需要确保分裂开的两节点都至少有一个元素 538 // K parentKey = null; 539 // int m = (tmpSizeIfInserted / 2); 540 // switch (inputDataOrder) { 541 // case ASCENDING: 542 // m = tmpSizeIfInserted - 2; 543 // break; 544 // case DESCENDING: 545 // m = 1; 546 // break; 547 // case RANDOM: 548 // default: 549 // m = (tmpSizeIfInserted / 2); 550 // break; 551 // } 552 // 553 // if (i == m) { 554 // parentKey = key; 555 // // 复制到新节点并删除原节点里相应的内容 556 // newNode.pointers[0] = rightChild; 557 // newNode.pointers[0].parent = newNode; 558 // for (int j = m; j < this.size; j++) { 559 // newNode.keys[j - m] = this.keys[j]; 560 // newNode.pointers[j + 1 - m] = this.pointers[j + 1]; 561 // newNode.pointers[j + 1 - m].parent = newNode; 562 // this.keys[j] = null; 563 // this.pointers[j + 1] = null; 564 // newNode.size++; 565 // } 566 // this.size = m; 567 // 568 // } else if (i < m) { 569 // parentKey = (K) this.keys[m - 1]; 570 // // 复制到新节点并删除原节点里相应的内容 571 // newNode.pointers[0] = this.pointers[m]; 572 // newNode.pointers[0].parent = newNode; 573 // for (int j = m; j < this.size; j++) { 574 // newNode.keys[j - m] = this.keys[j]; 575 // newNode.pointers[j + 1 - m] = this.pointers[j + 1]; 576 // newNode.pointers[j + 1 - m].parent = newNode; 577 // this.keys[j] = null; 578 // this.pointers[j + 1] = null; 579 // newNode.size++; 580 // } 581 // this.size = m; 582 // 583 // // 插入新内容到原节点 584 // for (int j = m - 1; j > i; j--) { 585 // this.keys[j] = this.keys[j - 1]; 586 // this.pointers[j + 1] = this.pointers[j]; 587 // } 588 // this.keys[i] = key; 589 // this.pointers[i + 1] = rightChild; 590 // } else { 591 // parentKey = (K) this.keys[m]; 592 // // 复制到新节点并删除原节点里相应的内容 593 // newNode.pointers[0] = this.pointers[m + 1]; 594 // newNode.pointers[0].parent = newNode; 595 // for (int j = m + 1; j < this.size; j++) { 596 // if (j == i) {// 复制插入的新内容 597 // newNode.keys[newNode.size] = key; 598 // newNode.pointers[newNode.size + 1] = rightChild; 599 // newNode.size++; 600 // } 601 // // 复制原节点的内容 602 // newNode.keys[newNode.size] = this.keys[j]; 603 // newNode.pointers[newNode.size + 1] = this.pointers[j + 1]; 604 // newNode.pointers[newNode.size + 1].parent = newNode; 605 // this.keys[j] = null; 606 // this.pointers[j + 1] = null; 607 // newNode.size++; 608 // } 609 // if (i == this.size) {// 复制插入的新内容 610 // newNode.keys[newNode.size] = key; 611 // newNode.pointers[newNode.size + 1] = rightChild; 612 // newNode.size++; 613 // } 614 // this.size = m; 615 // } 616 // 617 // if (this.parent == null) { 618 // this.parent = new InternalNode<K, V>(); 619 // } 620 // newNode.parent = this.parent; 621 // 622 // // 更新节点间的相邻关系 623 // newNode.next = this.next; 624 // newNode.previous = this; 625 // if (this.next != null) { 626 // this.next.previous = newNode; 627 // } 628 // this.next = newNode; 629 // 630 // return ((InternalNode<K, V>) this.parent).insert(parentKey, this, newNode); 631 } 632 633 // 原实现 634 System.arraycopy(this.keys, 0, tmpNewKeys, 0, i); 635 tmpNewKeys[i] = key; 636 System.arraycopy(this.keys, i, tmpNewKeys, i + 1, this.size - i); 637 638 System.arraycopy(this.pointers, 0, tmpNewPointers, 0, i + 1); 639 tmpNewPointers[i + 1] = rightChild; 640 System.arraycopy(this.pointers, i + 1, tmpNewPointers, i + 2, this.size - i); 641 642 this.size++; 643 644 // 要被提到父节点的key的下标,需要确保分裂开的两节点都至少有一个元素 645 int m = (this.size / 2); 646 switch (inputDataOrder) { 647 case ASCENDING: 648 m = this.size - 2; 649 break; 650 case DESCENDING: 651 m = 1; 652 break; 653 case RANDOM: 654 default: 655 m = (this.size / 2); 656 break; 657 } 658 659 // split the internal node 660 InternalNode<K, V> newNode = new InternalNode<K, V>(); 661 662 newNode.size = this.size - m - 1; 663 System.arraycopy(tmpNewKeys, m + 1, newNode.keys, 0, newNode.size); 664 System.arraycopy(tmpNewPointers, m + 1, newNode.pointers, 0, newNode.size + 1); 665 666 // reset the children's parent to the new node. 667 for (int j = 0; j <= newNode.size; j++) { 668 newNode.pointers[j].parent = newNode; 669 } 670 671 this.size = m; 672 673 System.arraycopy(tmpNewKeys, 0, this.keys, 0, m); 674 System.arraycopy(tmpNewPointers, 0, this.pointers, 0, m + 1); 675 676 if (this.parent == null) { 677 this.parent = new InternalNode<K, V>(); 678 } 679 newNode.parent = this.parent; 680 681 // 更新节点间的相邻关系 682 newNode.next = this.next; 683 newNode.previous = this; 684 if (this.next != null) { 685 this.next.previous = newNode; 686 } 687 this.next = newNode; 688 689 // tmpNewKeys[m]作为新key插入父节点,此key在分裂后的两个节点中都不存在 690 return ((InternalNode<K, V>) this.parent).insert((K) tmpNewKeys[m], this, newNode); 691 } 692 } 693 694 /** 695 * 下层节点在触发合并操作时才会进入此方法。rightChild丢弃、key删掉 696 * 697 * @return 若树高度降低导致产生新根节点则返回该新根节点,否则返回null 698 */ 699 private Node<K, V> remove(K key, Node<K, V> leftChil3d, Node<K, V> rightCh6ild) { 700 // TODO Auto-generated method stub 701 702 // 找key的位置 703 int i; 704 for (i = 0; i < this.size; i++) { 705 if (key.compareTo((K) this.keys[i]) == 0) { 706 break; 707 } 708 } 709 710 // 没找到,结束 711 if (i == this.size) { 712 return null; 713 } 714 715 // 找到,删除key对应的记录、指向合并后被丢弃的子节点(即rightChild也即this.pointers[i + 1])的指针置空 716 for (; i < this.size - 1; i++) { 717 this.keys[i] = this.keys[i + 1]; 718 this.pointers[i + 1] = this.pointers[i + 2]; 719 } 720 // System.out.println("**internal remove " + key + " in " + i + " of " + this.toString()); 721 this.keys[this.size - 1] = null; 722 this.pointers[this.size] = null; 723 this.size--; 724 725 /* 以下进行调整 */ 726 727 // 当前层只有一个节点的情况,为根节点 728 if (this.previous == null && this.next == null) { 729 if (this.size == 0) {// 减少一层 730 Node<K, V> newRoot = (Node<K, V>) (this.pointers[0]); 731 newRoot.parent = null; 732 return newRoot; 733 } else { 734 return null; 735 } 736 } 737 // 以下分支:当前节点有兄弟节点 738 739 else if (this.size >= (MIN_CHILDREN_FOR_INTERNAL - 1)) {// 无须借位、合并,结束 740 return null; 741 } 742 // 以下分支:当前节点有兄弟节点,且删后当前节点的键数为(MIN_CHILDREN_FOR_INTERNAL - 2),需要借位或合并 743 744 else if (this.previous != null && (this.previous.parent == this.parent) 745 && this.previous.size > (MIN_CHILDREN_FOR_INTERNAL - 1)) {// 从前一兄弟节点借一个元素 746 InternalNode<K, V> borrowedNode = (InternalNode<K, V>) this.previous; 747 748 /** 设this和previous在parent的分界键为key_parent,previous的最后一键和指针为key_last、pointer_last,则将key_parent、pointer_last作为新元素插入到this首位且将key_last替代parent的key_parent */ 749 int j; 750 // 后挪空出首位 751 for (j = this.size; j > 0; j--) { 752 this.keys[j] = this.keys[j - 1]; 753 this.pointers[j + 1] = this.pointers[j]; 754 } 755 this.pointers[1] = this.pointers[0]; 756 757 // 找出父节点key所在位置 758 Node<K, V> parent = this.parent; 759 K tmpKey = (this.size == 0) ? key : (K) this.keys[1]; 760 for (j = parent.size - 1; j >= 0; j--) { 761 if (tmpKey.compareTo((K) (parent.keys[j])) > 0) { 762 break; 763 } 764 } 765 766 // 借位操作 767 this.keys[0] = parent.keys[j]; 768 this.pointers[0] = borrowedNode.pointers[borrowedNode.size]; 769 this.pointers[0].parent = this; 770 this.size++; 771 parent.keys[j] = borrowedNode.keys[borrowedNode.size - 1]; 772 borrowedNode.keys[borrowedNode.size - 1] = null; 773 borrowedNode.pointers[borrowedNode.size] = null; 774 borrowedNode.size--; 775 776 return null; 777 778 } else if (this.next != null && (this.next.parent == this.parent) 779 && this.next.size > (MIN_CHILDREN_FOR_INTERNAL - 1)) {// 从后一个兄弟节点借一个元素 780 InternalNode<K, V> borrowedNode = (InternalNode<K, V>) this.next; 781 782 // 找出父节点key所在位置 783 int j; 784 Node<K, V> parent = this.parent; 785 K tmpKey = (K) borrowedNode.keys[0]; 786 for (j = parent.size - 1; j >= 0; j--) { 787 if (tmpKey.compareTo((K) (parent.keys[j])) > 0) { 788 break; 789 } 790 } 791 792 // 借位操作 793 this.keys[this.size] = parent.keys[j]; 794 this.pointers[this.size + 1] = borrowedNode.pointers[0]; 795 this.pointers[this.size + 1].parent = this; 796 this.size++; 797 parent.keys[j] = borrowedNode.keys[0]; 798 799 for (j = 0; j < borrowedNode.size - 1; j++) { 800 borrowedNode.keys[j] = borrowedNode.keys[j + 1]; 801 borrowedNode.pointers[j] = borrowedNode.pointers[j + 1]; 802 } 803 borrowedNode.pointers[j] = borrowedNode.pointers[j + 1]; 804 borrowedNode.keys[borrowedNode.size - 1] = null; 805 borrowedNode.pointers[borrowedNode.size] = null; 806 borrowedNode.size--; 807 808 return null; 809 810 } else if (this.previous != null && (this.previous.parent == this.parent) 811 && this.previous.size == (MIN_CHILDREN_FOR_INTERNAL - 1)) {// 与前一兄弟节点合并。(其实只会=,不会<) 812 // parent中的分界key复制到前一节点末尾后当前节点内容复制到前一节点 813 // 合并后目标节点的size为(MIN_CHILDREN_FOR_INTERNAL - 1) +1+ (MIN_CHILDREN_FOR_INTERNAL - 2) 814 815 InternalNode<K, V> previous = (InternalNode<K, V>) this.previous; 816 817 // 找出父节点分界key所在位置 818 Node<K, V> parent = this.parent; 819 K tmpKey = this.size == 0 ? key : (K) this.keys[0]; 820 int j; 821 for (j = parent.size - 1; j >= 0; j--) { 822 if (tmpKey.compareTo((K) (parent.keys[j])) > 0) { 823 break; 824 } 825 } 826 827 // 合并 828 previous.keys[previous.size] = parent.keys[j]; 829 previous.pointers[previous.size + 1] = this.pointers[0]; 830 this.pointers[0].parent = previous; 831 this.pointers[0] = null;// 复制过去后清空本节点的该元素 832 previous.size++; 833 for (int k = 0; k < this.size; k++) { 834 previous.keys[previous.size + k] = this.keys[k]; 835 previous.pointers[previous.size + k + 1] = this.pointers[k + 1]; 836 this.pointers[k + 1].parent = previous; 837 838 this.keys[k] = null;// 复制过去后清空本节点的该元素,下同 839 this.pointers[k + 1] = null; 840 } 841 previous.size += this.size; 842 this.size = 0;// 复制过去后清空本节点 843 844 // 更新节点相邻关系 845 previous.next = this.next; 846 if (this.next != null) { 847 this.next.previous = previous; 848 } 849 this.parent = null; 850 this.previous = null; 851 this.next = null; 852 853 return ((InternalNode<K, V>) previous.parent).remove((K) parent.keys[j], previous, this); 854 } else if (this.next != null && (this.next.parent == this.parent) 855 && this.next.size == (MIN_CHILDREN_FOR_INTERNAL - 1)) {// 与后一兄弟节点合并。(其实只会=,不会<) 856 // parent中的分界key复制到当前节点末尾后后一节点的内容复制到当前节点 857 // 合并后目标节点的size为(MIN_CHILDREN_FOR_INTERNAL - 1) +1+ (MIN_CHILDREN_FOR_INTERNAL - 2) 858 859 InternalNode<K, V> next = (InternalNode<K, V>) this.next; 860 861 // 找出父节点分界key所在位置 862 Node<K, V> parent = next.parent; 863 K tmpKey = (K) next.keys[0]; 864 int j; 865 for (j = parent.size - 1; j >= 0; j--) { 866 if (tmpKey.compareTo((K) (parent.keys[j])) > 0) { 867 break; 868 } 869 } 870 871 // 合并 872 this.keys[this.size] = parent.keys[j]; 873 this.pointers[this.size + 1] = next.pointers[0]; 874 next.pointers[0].parent = this; 875 next.pointers[0] = null;// 复制过去后清空本节点的该元素 876 this.size++; 877 for (int k = 0; k < next.size; k++) { 878 this.keys[this.size + k] = next.keys[k]; 879 this.pointers[this.size + k + 1] = next.pointers[k + 1]; 880 next.pointers[k + 1].parent = this; 881 882 next.keys[k] = null;// 复制过去后清空本节点的该元素,下同 883 next.pointers[k + 1] = null; 884 } 885 this.size += next.size; 886 next.size = 0;// 复制过去后清空本节点的该元素 887 888 // 更新节点相邻关系 889 this.next = next.next; 890 if (next.next != null) { 891 next.next.previous = this; 892 } 893 next.parent = null; 894 next.previous = null; 895 next.next = null; 896 897 return ((InternalNode<K, V>) this.parent).remove((K) parent.keys[j], this, next); 898 } else {// 永远到不了这 899 System.err.println("wrong in internal node remove."); 900 return null; 901 } 902 } 903 } 904 905 /** 906 * leaf node, store the keys and actual values. 907 * 908 * @param <K> 909 * @param <V> 910 */ 911 final class LeafNode<K extends Comparable<K>, V> extends Node<K, V> { 912 private Object[] values; 913 914 public LeafNode() { 915 this.size = 0; 916 this.keys = new Object[MAX_CHILDREN_FOR_LEAF]; 917 this.values = new Object[MAX_CHILDREN_FOR_LEAF]; 918 this.parent = null; 919 920 this.previous = null; 921 this.next = null; 922 } 923 924 @Override 925 protected V get(K key) { 926 // two branch search 927 if (this.size == 0) { 928 return null; 929 } 930 931 int s = 0, e = this.size - 1; 932 int m = -1; 933 K mKey = null; 934 boolean isFind = false; 935 while (s <= e) { 936 m = (s + e) / 2; 937 mKey = (K) this.keys[m]; 938 if (key.compareTo(mKey) == 0) { 939 isFind = true; 940 break; 941 } else if (key.compareTo(mKey) > 0) { 942 s = m + 1; 943 } else { 944 e = m - 1; 945 } 946 } 947 return isFind ? ((V) this.values[m]) : null; 948 } 949 950 @Override 951 protected Node<K, V> insert(K key, V value) { 952 int i = 0; 953 for (; i < this.size; i++) { 954 K curKey = (K) this.keys[i]; 955 if (curKey.compareTo(key) == 0) {// key已存在,更新值 956 this.values[i] = value; 957 return null; 958 } 959 if (curKey.compareTo(key) > 0) 960 break; 961 } 962 963 dataCount++; 964 // 以下分支:key不存在,插入新key-value 965 966 // 未满,直接插入 967 if (this.size + 1 <= MAX_CHILDREN_FOR_LEAF) { 968 for (int j = this.size; j > i; j--) { 969 this.keys[j] = this.keys[j - 1]; 970 this.values[j] = this.values[j - 1]; 971 } 972 this.keys[i] = key; 973 this.values[i] = value; 974 this.size++; 975 return null; 976 } 977 // 以下分支:插入后会满 978 // 979 else if (this.previous != null && (this.previous.parent == this.parent) 980 && this.previous.size < MAX_CHILDREN_FOR_LEAF) {// 旋转操作:放一个到前一兄弟节点 981 // 找到父节点中分界key的位置 982 Node<K, V> parent = this.parent; 983 K tmpKey = (K) this.keys[0]; 984 int j; 985 for (j = parent.size - 1; j >= 0; j--) { 986 if (tmpKey.compareTo((K) (parent.keys[j])) >= 0) {// 若维护叶节点第一个key等于父节点分界key,则只会= 987 break; 988 } 989 } 990 991 // 把当前节点的一个元素放到目标兄弟节点后在当前节点插入key-value,并更新父节点key 992 LeafNode<K, V> toNode = (LeafNode<K, V>) this.previous; 993 if (i == 0) {// 按理应插入到当前节点首位 994 toNode.keys[toNode.size] = key; 995 toNode.values[toNode.size] = value; 996 toNode.size++; 997 } else { 998 toNode.keys[toNode.size] = this.keys[0]; 999 toNode.values[toNode.size] = this.values[0]; 1000 toNode.size++; 1001 1002 // 移掉一个元素到目的节点后,待插元素应放在i-1的位置 1003 int insertPos = i - 1; 1004 for (int k = 0; k < insertPos; k++) { 1005 this.keys[k] = this.keys[k + 1]; 1006 this.values[k] = this.values[k + 1]; 1007 } 1008 this.keys[insertPos] = key; 1009 this.values[insertPos] = value; 1010 } 1011 1012 // 更新它们的父节点的分界key 1013 parent.keys[j] = this.keys[0]; 1014 1015 return null; 1016 1017 } else if (this.next != null && (this.next.parent == this.parent) 1018 && this.next.size < MAX_CHILDREN_FOR_LEAF) {// 旋转操作: 放一个到下一兄弟节点 1019 LeafNode<K, V> toNode = (LeafNode<K, V>) this.next; 1020 // 找到父节点中分界key的位置 1021 Node<K, V> parent = this.parent; 1022 K tmpKey = (K) toNode.keys[0]; 1023 int j; 1024 for (j = parent.size - 1; j >= 0; j--) { 1025 if (tmpKey.compareTo((K) (parent.keys[j])) >= 0) {// 若维护叶节点第一个key等于父节点分界key,则只会= 1026 break; 1027 } 1028 } 1029 1030 // 腾出首位 1031 for (int k = toNode.size; k > 0; k--) { 1032 toNode.keys[k] = toNode.keys[k - 1]; 1033 toNode.values[k] = toNode.values[k - 1]; 1034 } 1035 toNode.size++; 1036 1037 // 把当前节点的一个元素放到目标兄弟节点后在当前节点插入key-value,并更新父节点key 1038 if (i == this.size) { 1039 toNode.keys[0] = key; 1040 toNode.values[0] = value; 1041 } else { 1042 toNode.keys[0] = this.keys[this.size - 1]; 1043 toNode.values[0] = this.values[this.size - 1]; 1044 1045 for (int k = this.size - 1; k > i; k--) { 1046 this.keys[k] = this.keys[k - 1]; 1047 this.values[k] = this.values[k - 1]; 1048 } 1049 this.keys[i] = key; 1050 this.values[i] = value; 1051 } 1052 // 更新它们的父节点的分界key 1053 parent.keys[j] = toNode.keys[0]; 1054 1055 return null; 1056 1057 } else {// 进行分裂 1058 1059 { 1060 // LeafNode<K, V> newNode = new LeafNode<K, V>(); 1061 // int tmpSizeIfInserted = this.size + 1; 1062 // // 如果插入后需要被提到父节点的key及其下标,需要确保分裂开的两节点都至少有一个元素 1063 // K parentKey = null; 1064 // int m = (tmpSizeIfInserted / 2); 1065 // switch (inputDataOrder) { 1066 // case ASCENDING: 1067 // m = tmpSizeIfInserted - 1; 1068 // break; 1069 // case DESCENDING: 1070 // m = 1; 1071 // break; 1072 // case RANDOM: 1073 // default: 1074 // m = (tmpSizeIfInserted / 2); 1075 // break; 1076 // } 1077 // 1078 // if (i == m) { 1079 // parentKey = key; 1080 // // 复制到新节点并删除原节点里相应的内容 1081 // newNode.keys[0] = key; 1082 // newNode.values[0] = value; 1083 // newNode.size++; 1084 // for (int j = m; j < this.size; j++) { 1085 // newNode.keys[j - m + 1] = this.keys[j]; 1086 // newNode.values[j - m + 1] = this.values[j]; 1087 // this.keys[j] = null; 1088 // this.values[j] = null; 1089 // newNode.size++; 1090 // } 1091 // this.size = m; 1092 // 1093 // } else if (i < m) { 1094 // parentKey = (K) this.keys[m - 1]; 1095 // // 复制到新节点并删除原节点里相应的内容 1096 // for (int j = m - 1; j < this.size; j++) { 1097 // newNode.keys[j - m + 1] = this.keys[j]; 1098 // newNode.values[j - m + 1] = this.values[j]; 1099 // this.keys[j] = null; 1100 // this.values[j] = null; 1101 // newNode.size++; 1102 // } 1103 // this.size = m; 1104 // 1105 // // 插入新内容到原节点 1106 // for (int j = m - 1; j > i; j--) { 1107 // this.keys[j] = this.keys[j - 1]; 1108 // this.values[j] = this.values[j - 1]; 1109 // } 1110 // this.keys[i] = key; 1111 // this.values[i] = value; 1112 // } else { 1113 // parentKey = (K) this.keys[m]; 1114 // // 复制到新节点并删除原节点里相应的内容 1115 // for (int j = m; j < this.size; j++) { 1116 // if (j == i) {// 复制插入的新内容 1117 // newNode.keys[newNode.size] = key; 1118 // newNode.values[newNode.size] = value; 1119 // newNode.size++; 1120 // } 1121 // // 复制原节点的内容 1122 // newNode.keys[newNode.size] = this.keys[j]; 1123 // newNode.values[newNode.size] = this.values[j]; 1124 // this.keys[j] = null; 1125 // this.values[j] = null; 1126 // newNode.size++; 1127 // } 1128 // if (i == this.size) {// 复制插入的新内容 1129 // newNode.keys[newNode.size] = key; 1130 // newNode.values[newNode.size] = value; 1131 // newNode.size++; 1132 // } 1133 // this.size = m; 1134 // } 1135 // if (this.parent == null) {// 只有在刚开始只有一个叶节点且叶节点已满时才成立 1136 // this.parent = new InternalNode<K, V>(); 1137 // } 1138 // newNode.parent = this.parent; 1139 // 1140 // // 更新叶节点的相邻关系 1141 // newNode.next = this.next; 1142 // newNode.previous = this; 1143 // if (this.next != null) { 1144 // this.next.previous = newNode; 1145 // } 1146 // this.next = newNode; 1147 // 1148 // return ((InternalNode<K, V>) this.parent).insert(parentKey, this, newNode); 1149 } 1150 1151 // 原实现 1152 System.arraycopy(this.keys, 0, tmpNewKeys, 0, i); 1153 tmpNewKeys[i] = key; 1154 System.arraycopy(this.keys, i, tmpNewKeys, i + 1, this.size - i); 1155 1156 System.arraycopy(this.values, 0, tmpNewValues, 0, i); 1157 tmpNewValues[i] = value; 1158 System.arraycopy(this.values, i, tmpNewValues, i + 1, this.size - i); 1159 1160 this.size++; 1161 1162 // need split this node 1163 int m = this.size / 2; 1164 switch (inputDataOrder) { 1165 case ASCENDING: 1166 m = this.size - 1; 1167 break; 1168 case DESCENDING: 1169 m = 1; 1170 break; 1171 case RANDOM: 1172 default: 1173 m = (this.size / 2); 1174 break; 1175 } 1176 1177 LeafNode<K, V> newNode = new LeafNode<K, V>(); 1178 newNode.size = this.size - m; 1179 System.arraycopy(tmpNewKeys, m, newNode.keys, 0, newNode.size); 1180 System.arraycopy(tmpNewValues, m, newNode.values, 0, newNode.size); 1181 1182 this.size = m; 1183 System.arraycopy(tmpNewKeys, 0, this.keys, 0, m); 1184 System.arraycopy(tmpNewValues, 0, this.values, 0, m); 1185 1186 if (this.parent == null) {// 只有在刚开始只有一个叶节点且叶节点已满时才成立 1187 this.parent = new InternalNode<K, V>(); 1188 } 1189 newNode.parent = this.parent; 1190 1191 // 更新叶节点的相邻关系 1192 newNode.next = this.next; 1193 newNode.previous = this; 1194 if (this.next != null) { 1195 this.next.previous = newNode; 1196 } 1197 this.next = newNode; 1198 1199 // 清理无用引用,使GC能回收 1200 1201 // tmpNewKeys[m]作为新key插入父节点,此key也作为分裂后后节点的第一个元素 1202 return ((InternalNode<K, V>) this.parent).insert((K) newNode.keys[0], this, newNode); 1203 } 1204 } 1205 1206 @Override 1207 protected Node<K, V> remove(K key) { 1208 // TODO Auto-generated method stub 1209 1210 // 查找key的位置 1211 int i; 1212 for (i = 0; i < this.size; i++) { 1213 if (key.compareTo((K) this.keys[i]) == 0) { 1214 break; 1215 } 1216 } 1217 1218 // 没找到,结束 1219 if (i == this.size) { 1220 return null; 1221 } 1222 1223 // 找到,删除key对应的记录 1224 for (int j = i; j < this.size - 1; j++) { 1225 this.keys[j] = this.keys[j + 1]; 1226 this.values[j] = this.values[j + 1]; 1227 } 1228 // System.out.println("**leaf remove " + key + " in " + i + " of " + this.toString()); 1229 this.keys[this.size - 1] = null; 1230 this.values[this.size - 1] = null; 1231 this.size--; 1232 1233 dataCount--; 1234 1235 /* 以下进行调整 */ 1236 1237 // 树只有此叶节点,无须借位、合并,结束 1238 if (this.parent == null) { 1239 return null; 1240 } 1241 // 且 删后记录数不少于一半,无需借位、合并,结束 1242 else if (this.size >= MIN_CHILDREN_FOR_LEAF) { 1243 if (i == 0) {// 可选操作:删除了第一个元素,因此需要维持叶节点第一个key与父节点的一个key一样 1244 Node<K, V> parent = this.parent; 1245 K tmpKey = (K) this.keys[0]; 1246 for (int j = parent.size - 1; j >= 0; j--) { 1247 if (tmpKey.compareTo((K) (parent.keys[j])) >= 0) {// 只会> 1248 parent.keys[j] = this.keys[0]; 1249 break; 1250 } 1251 } 1252 } 1253 return null; 1254 } 1255 // 以下分支:有兄弟节点,且删后节点的键数为MIN_CHILDREN_FOR_LEAF-1,需要借位或合并:优先尝试借位,借位不成再合并。注意只有兄弟节点间才能借位或合并 1256 1257 else if (this.previous != null && (this.previous.parent == this.parent) 1258 && this.previous.size > MIN_CHILDREN_FOR_LEAF) {// 从前一兄弟节点借一个元素 1259 1260 LeafNode<K, V> borrowedNode = (LeafNode<K, V>) this.previous; 1261 1262 // 取上节点最后一个元素放到当前节点的第一个位置 1263 for (int j = this.size; j > 0; j--) { 1264 this.keys[j] = this.keys[j - 1]; 1265 this.values[j] = this.values[j - 1]; 1266 } 1267 this.keys[0] = borrowedNode.keys[borrowedNode.size - 1]; 1268 this.values[0] = borrowedNode.values[borrowedNode.size - 1]; 1269 this.size++; 1270 borrowedNode.keys[borrowedNode.size - 1] = null; 1271 borrowedNode.values[borrowedNode.size - 1] = null; 1272 borrowedNode.size--; 1273 1274 // 可选操作:更新父节点的key为借来的元素的key 1275 Node<K, V> parent = this.parent; 1276 K tmpKey = (this.size == 1) ? key : (K) this.keys[1]; 1277 for (int j = parent.size - 1; j >= 0; j--) { 1278 if (tmpKey.compareTo((K) (parent.keys[j])) >= 0) {// 若维护叶节点第一个key等于父节点分界key,则只会= 1279 parent.keys[j] = this.keys[0]; 1280 break; 1281 } 1282 } 1283 return null; 1284 1285 } else if (this.next != null && (this.next.parent == this.parent) 1286 && this.next.size > MIN_CHILDREN_FOR_LEAF) {// 从后一兄弟节点借一个元素 1287 1288 LeafNode<K, V> borrowedNode = (LeafNode<K, V>) this.next; 1289 1290 // 取下节点的第一个元素放到当前节点的最后一个位置 1291 this.keys[this.size] = borrowedNode.keys[0]; 1292 this.values[this.size] = borrowedNode.values[0]; 1293 this.size++; 1294 for (int j = 0, len = borrowedNode.size - 1; j < len; j++) { 1295 borrowedNode.keys[j] = borrowedNode.keys[j + 1]; 1296 borrowedNode.values[j] = borrowedNode.values[j + 1]; 1297 } 1298 borrowedNode.keys[borrowedNode.size - 1] = null; 1299 borrowedNode.values[borrowedNode.size - 1] = null; 1300 borrowedNode.size--; 1301 1302 // 可选操作:更新父节点的key为被借节点的新首元素 1303 Node<K, V> parent = this.parent; 1304 K tmpKey = (K) this.keys[this.size - 1]; 1305 for (int j = parent.size - 1; j >= 0; j--) { 1306 if ((tmpKey).compareTo((K) parent.keys[j]) >= 0) {// 若维护叶节点第一个key等于父节点分界key,则只会= 1307 parent.keys[j] = borrowedNode.keys[0]; 1308 break; 1309 } 1310 } 1311 return null; 1312 1313 } else if (this.previous != null && (this.previous.parent == this.parent) 1314 && this.previous.size == MIN_CHILDREN_FOR_LEAF) {// 与前一兄弟节点合并。(其实只会=,不会<) 1315 // 找出父节点分界key所在位置 1316 K dividKey = this.size == 0 ? key : (K) this.keys[0]; 1317 1318 // 当前节点的内容复制到前一节点,合并后目标节点的size为MIN_CHILDREN_FOR_LEAF + (MIN_CHILDREN_FOR_LEAF-1) 1319 LeafNode<K, V> previous = (LeafNode<K, V>) this.previous; 1320 for (int j = 0; j < this.size; j++) { 1321 previous.keys[previous.size + j] = this.keys[j]; 1322 previous.values[previous.size + j] = this.values[j]; 1323 1324 this.keys[j] = null;// 复制过去后清空本节点的该元素,下同 1325 this.values[j] = null; 1326 } 1327 previous.size += this.size; 1328 this.size = 0;// 复制过去后清空本节点的该元素 1329 1330 // 更新叶节点相邻关系 1331 previous.next = this.next; 1332 if (this.next != null) { 1333 this.next.previous = previous; 1334 } 1335 this.parent = null; 1336 this.previous = null; 1337 this.next = null; 1338 1339 // key及父节点中指向当前节点的poniter会在父节点执行删除方法时被覆盖,从而当前节点被删除 1340 return ((InternalNode<K, V>) previous.parent).remove(dividKey, previous, this); 1341 1342 } else if (this.next != null && (this.next.parent == this.parent) 1343 && this.next.size == MIN_CHILDREN_FOR_LEAF) {// 与后一兄弟节点合并。(其实只会=,不会<) 1344 // 找出父节点分界key所在位置 1345 K dividKey = (K) next.keys[0]; 1346 1347 // 后一节点的内容复制到当前节点,合并后目标节点的size为MIN_CHILDREN_FOR_LEAF + (MIN_CHILDREN_FOR_LEAF-1) 1348 LeafNode<K, V> next = (LeafNode<K, V>) this.next; 1349 for (int j = 0; j < next.size; j++) { 1350 this.keys[this.size + j] = next.keys[j]; 1351 this.values[this.size + j] = next.values[j]; 1352 1353 next.keys[j] = null;// 复制过去后清空本节点的该元素,下同 1354 next.values[j] = null; 1355 } 1356 this.size += next.size; 1357 next.size = 0;// 复制过去后清空本节点的该元素 1358 1359 // 更新叶节点相邻关系 1360 this.next = next.next; 1361 if (next.next != null) { 1362 next.next.previous = this; 1363 } 1364 next.parent = null; 1365 next.previous = null; 1366 next.next = null; 1367 1368 return ((InternalNode<K, V>) this.parent).remove(dividKey, this, next); 1369 } else {// 永远到不了这 1370 System.err.println("wrong in leaf node remove."); 1371 return null; 1372 } 1373 } 1374 } 1375 }

1 package buaa.act.ucar.imtg.index.node.temporal; 2 3 import java.lang.management.ManagementFactory; 4 import java.lang.management.MemoryMXBean; 5 import java.lang.management.MemoryUsage; 6 import java.text.SimpleDateFormat; 7 import java.util.Date; 8 import java.util.HashMap; 9 import java.util.Map; 10 import java.util.Random; 11 12 import buaa.act.ucar.imtg.index.node.temporal.BPlusTree.InputDataOrder; 13 import scala.collection.generic.BitOperations.Int; 14 15 /** 16 * @author zsm 17 * @date 2017年1月11日 上午11:24:58 18 */ 19 public class BPlusTreeTest { 20 public static void main(String[] args) { 21 BPlusTree<Integer, Integer> bPlusTree = new BPlusTree<>(5, InputDataOrder.RANDOM); 22 for (int i = 0; i < 100; i++) { 23 bPlusTree.set(i, i); 24 } 25 bPlusTree.remove(4); 26 bPlusTree.printTree(); 27 System.out.println(bPlusTree.getAllValues()); 28 } 29 30 public static void ma3in(String[] args) { 31 MemoryMXBean memorymbean = ManagementFactory.getMemoryMXBean(); 32 // memorymbean.setVerbose(true); 33 Runtime myRuntime = Runtime.getRuntime(); 34 35 long firinit, firused, fircommited, firmax; 36 long sedmax, sedtotal, sedfree, sedused; 37 double rad = 1024 * 1024.0; 38 SimpleDateFormat simpleDateFormat = new SimpleDateFormat("HH:mm:ss"); 39 Date date; 40 MemoryUsage usage; 41 42 BPlusTree<String, Integer> tree = new BPlusTree<>(5, InputDataOrder.RANDOM); 43 for (int j = 0; j < 60000; j++) { 44 for (int i = 10_000_000; i > 0; i--) { 45 // tree.set(i + "", i); 46 } 47 48 usage = memorymbean.getHeapMemoryUsage(); 49 date = new Date(); 50 firinit = usage.getInit(); 51 firused = usage.getUsed(); 52 fircommited = usage.getCommitted(); 53 firmax = usage.getMax(); 54 55 sedmax = myRuntime.maxMemory(); 56 sedtotal = myRuntime.totalMemory(); 57 sedfree = myRuntime.freeMemory(); 58 sedused = sedtotal - sedfree; 59 60 System.out.printf( 61 "by MemoryUsage: %s init(%dB≈%.4fMB), used(%dB≈%.4fMB), commited(%dB≈%.4fMB), max(%dB≈%.4fMB)\n", 62 simpleDateFormat.format(date), firinit, firinit / rad, firused, firused / rad, fircommited, 63 fircommited / rad, firmax, firmax / rad); 64 65 System.out.printf( 66 "by Runtime: %s free(%dB≈%.4fMB), used(%dB≈%.4fMB), total(%dB≈%.4fMB), max(%dB≈%.4fMB)\n", 67 simpleDateFormat.format(date), sedfree, sedfree / rad, sedused, sedused / rad, sedtotal, 68 sedtotal / rad, sedmax, sedmax / rad); 69 System.out.println(); 70 try { 71 Thread.sleep(4000); 72 } catch (InterruptedException e) { 73 // TODO Auto-generated catch block 74 e.printStackTrace(); 75 } 76 } 77 78 // System.err.println("add:"); 79 // for (int i = 1; i <= 41; i++) { 80 // tree.set(i, i); 81 // tree.printTree(tree.getRoot()); 82 // } 83 // System.out.println("height:" + tree.getHeight()); 84 // tree.printTree(tree.getRoot()); 85 // 86 // System.err.println("remove:"); 87 // tree.remove(21); 88 // tree.printTree(tree.getRoot()); 89 // tree.remove(22); 90 // tree.printTree(tree.getRoot()); 91 // tree.remove(23); 92 // tree.printTree(tree.getRoot()); 93 94 // test2(); 95 } 96 97 public static int getRandom(int min, int max, boolean isMaxInclude) { 98 return new Random().nextInt(max - min + (isMaxInclude ? 1 : 0)) + min; 99 } 100 101 /** 随机产生数据,并进行查询、删除 */ 102 public static void test2() { 103 BPlusTree<Integer, Integer> myTree = new BPlusTree<Integer, Integer>(10, InputDataOrder.RANDOM); 104 105 int max = 10_000_000; 106 int min = -max; 107 int numCount = max - min + 1; 108 int numRealCount = 0; 109 110 Integer[] data = new Integer[max - min + 1]; 111 for (int i = 0; i < data.length; i++) { 112 data[i] = 0; 113 } 114 115 // 产生数据 116 long start = System.currentTimeMillis(); 117 int key; 118 for (int i = 0; i < numCount; i++) { 119 key = getRandom(min, max, true); 120 // key = i + min; 121 // try { 122 // Thread.sleep(1000); 123 // } catch (InterruptedException e) { 124 // // TODO Auto-generated catch block 125 // e.printStackTrace(); 126 // } 127 myTree.set(key, key); 128 if (data[key - min] == 0) { 129 numRealCount++; 130 data[key - min] = 1; 131 } 132 } 133 System.out.println( 134 numRealCount + " data from " + numCount + "[" + min + "," + max + "] has been inserted into tree"); 135 System.out.println("time cost for insert: " + (System.currentTimeMillis() - start)); 136 System.out.println("tree leaf entry: " + myTree.getDataCount() + ", hashmap count:" + numRealCount); 137 138 // 查数据 139 System.out.println(); 140 System.out.println("getDataCount:" + myTree.getDataCount()); 141 System.out.println("height:" + myTree.getHeight()); 142 start = System.currentTimeMillis(); 143 int getCount = 0; 144 for (int i = 0; i < data.length; i++) { 145 if (data[i] == 1) { 146 getCount++; 147 key = i + min; 148 if (!myTree.get(key).equals(key)) { 149 System.err.println("error for get: " + myTree.get(key) + " " + key); 150 System.exit(1); 151 } 152 } 153 } 154 System.out.println("time cost for " + getCount + " get: " + (System.currentTimeMillis() - start)); 155 156 // 删除数据 157 System.out.println(); 158 start = System.currentTimeMillis(); 159 System.out.println(myTree.getDataCount()); 160 for (int i = data.length; i >= 0; i--) { 161 try { 162 myTree.remove(i + min); 163 } catch (Exception e) { 164 // TODO: handle exception 165 System.err.println(String.format("remove error: i=%d, key=%d \n", i, i + min)); 166 e.printStackTrace(); 167 System.exit(0); 168 } 169 } 170 System.out.println("getDataCount:" + myTree.getDataCount()); 171 System.out.println("height:" + myTree.getHeight()); 172 myTree.printTree(); 173 myTree.remove(-2); 174 System.out.println("time cost for remove: " + (System.currentTimeMillis() - start)); 175 } 176 177 public static void test1() { 178 BPlusTree<Integer, Integer> myTree = new BPlusTree<Integer, Integer>(8, InputDataOrder.RANDOM); 179 180 int max = 200 * 25000; 181 long start = System.currentTimeMillis(); 182 for (int i = 0; i < max; i++) { 183 myTree.set(i, i); 184 } 185 System.out.println(max + " Data has been inserted into tree"); 186 System.out.println("time cost for BPlusTree: " + (System.currentTimeMillis() - start)); 187 188 System.out.println(); 189 System.out.println("height: " + myTree.getHeight()); 190 System.out.println(myTree.get(2345)); 191 System.out.println(); 192 193 start = System.currentTimeMillis(); 194 for (int i = 0; i < max; i++) { 195 myTree.get(i); 196 } 197 System.out.println("time cost for get: " + (System.currentTimeMillis() - start)); 198 199 start = System.currentTimeMillis(); 200 Map<Integer, String> hashMap = new HashMap<Integer, String>(); 201 for (int i = 0; i < max; i++) { 202 hashMap.put(i, i + ""); 203 } 204 System.out.println("time cost for HashMap: " + (System.currentTimeMillis() - start)); 205 206 for (int i = 0; i < max; i++) { 207 if (myTree.get(i) != i) { 208 System.err.println("error for: " + i); 209 } 210 } 211 212 System.out.println("Success"); 213 214 // myTree.remove(2); 215 // myTree.printTree(myTree.getRoot()); 216 } 217 218 public static void test3() { 219 BPlusTree<Integer, String> myTree = new BPlusTree<Integer, String>(3, InputDataOrder.RANDOM); 220 221 int max = 7; 222 for (int i = 0; i < max; i++) { 223 // System.out.println("__insert " + i); 224 myTree.set(i, i + ""); 225 // myTree.printTree(myTree.getRoot()); 226 // System.out.println(); 227 228 // System.out.println("__insert " + (2 * max - i)); 229 myTree.set(2 * max - i, 2 * max - i + ""); 230 // myTree.printTree(myTree.getRoot()); 231 // System.out.println(); 232 } 233 234 System.out.println("tree height:" + myTree.getHeight()); 235 System.out.println("leaf entry count:" + myTree.getDataCount()); 236 System.out.println(); 237 238 myTree.printTree(); 239 System.out.println(); 240 241 for (int i = 0; i < max; i++) { 242 System.out.println("__remove " + i); 243 myTree.remove(i); 244 myTree.printTree(); 245 246 System.out.println("__remove " + (2 * max - i)); 247 myTree.remove(2 * max - i); 248 myTree.printTree(); 249 System.out.println(); 250 } 251 252 } 253 254 }
6、二叉树的应用
线段树 segment tree (参阅这篇文章),用于解决频繁查询数组不同区间的统计值(如最大、最小、和等)的问题,且支持动态修改数组数据。
原理:很简单,是一种树形结构(通常是二叉树),每个节点表示一个区间内的统计值,一个父节点区间被各子节点均匀分割,叶节点是一个元素组成的区间。
有自底向上、自顶向下两种构造方式,前者便于人阅读后者适合编码实现。树示例:

参阅 https://lotabout.me/2018/segment-tree/ (1)自底向上 [0,15] 0 ┌───────────────┴───────────────┐ [0,7] [8,15] 0 3 ┌───────┴───────┐ ┌───────┴───────┐ [0,3] [4,7] [8,11] 0 1 3 ┌───┴───┐ ┌───┴───┐ ┌───┴───┐ ┌───┴───┐ [0,1] [2,3] [4,5] [6,7] [8,9] 0 2 3 1 3 ┌─┴─┐ ┌─┴─┐ ┌─┴─┐ ┌─┴─┐ ┌─┴─┐ ┌─┴─┐ ┌─┴─┐ ┌─┴─┐ 0 5 2 5 4 3 1 6 3 ┬───┬───┬───┬───┬───┬───┬───┬───┬───┬───┬───┬───┬───┬───┬───┬─── 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 (2)自顶向下 [0,8] 0 ┌───────────────┴───────────────┐ [0,4] [5,8] 0 1 ┌───────┴───────┐ ┌───────┴───────┐ [0,2] [3,4] [5,6] [7,8] 0 4 1 3 ┌───┴───┐ ┌───┴───┐ ┌───┴───┐ ┌───┴───┐ [0,1] [2,2] [3,3] [4,4] [5,5] [6,6] [7,7] [8,8] 0 2 5 4 3 1 6 3 ┌─┴─┐ [0,0] [1,1] 0 5
实现(自顶向下):

public class ArraySegmentTree<T> { private T tree[]; private T data[]; private Merger<T> merger; public interface Merger<T> { T merge(T a, T b); } public ArraySegmentTree(T[] arr, Merger<T> merger) { this.merger = merger; data = (T[]) new Object[arr.length]; for (int i = 0; i < data.length; i++) { data[i] = arr[i]; } this.tree = (T[]) new Object[data.length * 4]; buildSegmentTree(0, 0, data.length - 1); } /** * 构建线段树 * * @param treeIndex 当前需要添加节点的索引 * @param treeLeft treeIndex左边界 * @param treeRight treeIndex右边界 */ private void buildSegmentTree(int treeIndex, int treeLeft, int treeRight) { if (treeLeft == treeRight) { tree[treeIndex] = data[treeLeft]; return; } //当前节点左子树索引 int leftTreeIndex = getLeft(treeIndex); //当前节点右子树索引 int rightTreeIndex = getRight(treeIndex); //int mid = (left+right)/2; 如果left和right很大,可能会导致整型溢出 int mid = treeLeft + (treeRight - treeLeft) / 2; //构建左子树 buildSegmentTree(leftTreeIndex, treeLeft, mid); //构建右子树 buildSegmentTree(rightTreeIndex, mid + 1, treeRight); //当前节点存放的值 tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]); } public T query(int start, int end) { return query(0, 0, data.length - 1, start, end); } /** * @param treeIndex 当前查找的节点 * @param treeLeft treeIndex的左边界 * @param treeRight treeIndex的右边界 * @param queryL 用户需要查找的左边界 * @param queryR 用户需要查找的右边界 * @return */ private T query(int treeIndex, int treeLeft, int treeRight, int queryL, int queryR) { //1, 需要查找的范围完刚好在这个treeIndex节点的区间 if (treeLeft == queryL && treeRight == queryR) { return tree[treeIndex]; } //当前节点的区间的中间点 int mid = treeLeft + (treeRight - treeLeft) / 2; //左子树索引 int leftTreeIndex = getLeft(treeIndex); //右子树索引 int rightTreeIndex = getRight(treeIndex); //2, 需要查找的范围完全在左子树的区间里 if (queryR <= mid) { return query(leftTreeIndex, treeLeft, mid, queryL, queryR); } //3, 需要查找的范围完全在右子树区间里 if (queryL >= mid + 1) { return query(rightTreeIndex, mid + 1, treeRight, queryL, queryR); } //需要查找的范围一部分在左子树里,一部分在右子树中 T left = query(leftTreeIndex, treeLeft, mid, queryL, mid); T right = query(rightTreeIndex, mid + 1, treeRight, mid + 1, queryR); return merger.merge(left, right); } public void update(int index, T e) { data[index] = e; update(0, 0, data.length - 1, index, e); } private void update(int treeIndex, int treeLeft, int treeRight, int index, T e) { if (treeLeft == treeRight) { tree[treeIndex] = e; return; } int mid = treeLeft + (treeRight - treeLeft) / 2; int leftChildIndex = getLeft(treeIndex); int rightChildIndex = getRight(treeIndex); if (index <= mid) { update(leftChildIndex, treeLeft, mid, index, e); } else if (index >= mid + 1) { update(rightChildIndex, mid + 1, treeRight, index, e); } //更改完叶子节点后,还需要对他的所有祖辈节点更新 tree[treeIndex] = merger.merge(tree[leftChildIndex], tree[rightChildIndex]); } public T get(int index) { return data[0]; } public int size() { return data.length; } public int getLeft(int index) { return index * 2 + 1; } public int getRight(int index) { return index * 2 + 2; } @Override public String toString() { StringBuilder builder = new StringBuilder(); builder.append("["); for (int i = 0; i < tree.length; i++) { if (tree[i] == null) { continue; } builder.append(tree[i]).append(','); } builder.deleteCharAt(builder.length() - 1); builder.append(']'); return builder.toString(); } }
时间复杂度:
区间统计问题通常用动态规划也能解但整体时间复杂度通常为O(n2),有些可优化为O(n);有些问题用前缀和数组也能解,甚至效率比线段树的高。但动规和前缀和不支持动态修改数组。
构造线段树的时间复杂度为O(n)、之后查询的时间复杂度为树高O(lgn)、元素变更导致的动态维护的时间复杂度为O(lgn);动规的分别为O(n2)、O(1)、O(n2);前缀和的分别为O(n)、O(1)、O(n)。动规和前缀和的动态维护其实就是完全重建。
二叉索引树 Binary Indexed Tree,用于解决允许动态修改的数组的前缀和问题。可见这种问题也可用线段树解决。详见 binary indexed tree。
初始化时间复杂度为O(nlgn)或O(n) ,取决于实现,查询和修改的时间复杂度为O(lgn) 。
7、拓展——其他特殊的树(不一定是二叉树)
用于字符串查找的树:
Trie Tree:前缀树,实践见 用Java实现Trie树-MarchOn。
Radix Tree(compact prefix tree),Trie树的改进,只有一个元素的路径会被合并在一起,因此树高会大大减少从而减少空间占用,但插入、删除、查找过程会变得稍微复杂点。
优点:查找时不仅支持精确查找,还支持查找前续字符串、后续字符串、某个前缀的所有字符串等;占用空间比Trie Tree。
使用场景:元素个数不是太多,但是元素之间通常有很长的相同前缀时很适合采用radix tree来存储。例如 IP routing(因为IP有地址有大量的公共前缀)、文本倒排索引中等。Redis中的字符串就用这种来索引。
Radix树与Trie树比较:两者思想类似,可把Trie树看成是一个基为26(英文字符个数)的Radix树(也可以把radix树看做是Trie树的变异)。Trie树一般用于字符串到对象的映射,而radix树一般用于长整数到对象的映射。Trie树主要问题是树的层高。假设要索引的字符串长度非常长,我们也要建一颗非常高的树么? radix树能固定层高(对于较长的字符串,能够用数学公式计算出其特征值,再用radix树存储这些特征值)。
一个开源实现:https://github.com/hlyzsm/rax,Redis 中采用的Radix Tree C实现。
树形结构的可选替代者-SkipList
(add on 20191216)
(关于SkipList详情可参阅:Redis跳表、https://lotabout.me/2018/skip-list、Implementation in c:https://gist.github.com/zhpengg/2873424)
树行结构缺点:原理和实现复杂(在节点增减或修改时可能需要进行旋转等调整操作,这是个费时的操作);对并发操作的支持差。
鉴于这些缺点,有了SkipList(跳表)。SkipList由William Pugh于1990年在 Communications of the ACM June 1990, 33(6) 668-676 发表的《Skip lists: a probabilistic alternative to balanced trees》paper中提出,SkipList的设计初衷是作为替换平衡树的一种选择,是一种包含多层有序单链表的随机化的数据结构。
原理:
从形态上看是一种包含多层有序单链表的结构,链表单向或双向均可,取决于实现。最低层包含所有元素、在最低层的基础上自底向上创建多层的有序单链表,上层的元素来源于下层但个数比下层少,起到“路标”或“索引”的作用。这样查询时从上层开始可跳过大部分元素从而减少节点比较;增删时与查询类似先自顶向下定位到最低层的节点位置接着操作然后维护上层链表。
示例:下图是比较理想的情况,上层节点数是下层的一半,实际上不会这么理想因为有随机因素,但即使非理想状态下平均时间复杂度也是O(lgn)。当然,最坏是只有一个单链表,此时是O(n)。

也是一种随机化的数据结构,体现在节点插入后要不要出现在上层、出现上面多少层由“抛硬币”决定。故从统计上来说一个skiplist结构的形成与节点的插入顺序无关。

randomLevel() #通过随机决定出现在多少层上。p表示一个key出现当前层时出现在直接上层的概率、MaxLevel表示整个skiplist最大允许的层数 level := 1 // random()返回一个[0...1)的随机数 while random() < p and level < MaxLevel do level := level + 1 return level
示例: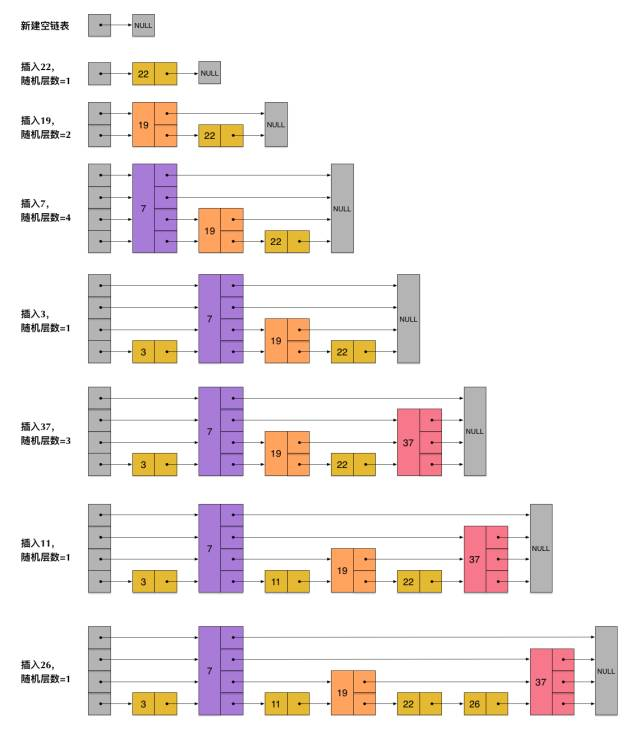
可见本质上与B+树有点像,体现在:都是自底向上增长;后者叶节点相连而前者内部同层节点也相连;后者每个非叶节点有多个key、多个子节点而前者上层节点只有一个key、一个子节点。
实现:
todo ...
性能:
与红黑树等平衡树相比,增删改查平均时间复杂度都是 O(lgn),但原理和实现简单(不用进行复杂的树节点分裂合并等)、范围查询简单(B+树范围查询也简单但红黑树就得改造才能支持通过中序遍历进行范围查询)。
时空复杂度(详细理论分析见本节首第一个参考文章):设插入一个节点到某层时出现在上一层的概率为p,则节点出现层数恰为i(i≥1)的概率为p(i-1)(1-p),故平均层数为1/(1-p)。进而可分析出(稍麻烦)时间复杂度为O(lgn)
应用:如Redis Zset(见 Redis Zset的实现-MarchOn)、LevelDB、LSM Tree中的MemTable等(后者在HBase、BigTable等很多地方用到)。与二叉树(AVL树)等相比性能更好,主要得益于插入、删除时不用进行复杂的树调整;查询时也有类似于树的navigator功能。
3、其他
1、二叉树与树、森林的转换
二叉树与一般树的双向转换、与森林的双向转换。(一般树转为二叉树后根节点度为1,包含多棵树的森林转为二叉树后根节点度为2)。二叉树转为树或森林时,该二叉树须是由后者转换而来的。
2、树、森林的遍历:
a、二叉树:前序、中序、后序、层次
b、树:前序、后序
c、森林:前序(即按树的前序遍历依次遍历每棵树)、中序(即按树的后序遍历方式依次遍历每棵树,尼玛叫后序更合适吧)
将树或森林转为二叉树或反向转换后:(不用记,举个例子就明了了)
二叉树的前序、树的前序、森林的前序遍历序列一样
二叉树的中序、树的后序、森林的中序(尼玛你若叫后序遍历这里就统一了)一样
3、森林的保存:
法1:用多个链表保存
法2:用一维数组parent[] 保存,parent[i]表示编号为i的节点的父节点编号。这实际上就是并查集的表示,关于并查集可参阅 UnionFind算法详解
附件——并查集代码:

class UF { // 连通分量个数 private int count; // 存储一棵树 private int[] parent; // 记录树的“重量” private int[] size; public UF(int n) { this.count = n; parent = new int[n]; size = new int[n]; for (int i = 0; i < n; i++) { parent[i] = i; size[i] = 1; } } public void union(int p, int q) { int rootP = find(p); int rootQ = find(q); if (rootP == rootQ) return; // 小树接到大树下面,较平衡 if (size[rootP] > size[rootQ]) { parent[rootQ] = rootP; size[rootP] += size[rootQ]; } else { parent[rootP] = rootQ; size[rootQ] += size[rootP]; } count--; } public boolean connected(int p, int q) { int rootP = find(p); int rootQ = find(q); return rootP == rootQ; } private int find(int x) { while (parent[x] != x) { // 进行路径压缩 parent[x] = parent[parent[x]]; x = parent[x]; } return x; } public int count() { return count; } }
4、二叉树题目的解决规律
二叉树题目的递归解法可以分两类思路,第一类是遍历一遍二叉树得出答案,第二类是通过分解问题计算出答案,这两类思路分别对应着 回溯算法核心框架 和 动态规划核心框架。详见labuladong-二叉树题目算法技巧总结。




