Splay简介

　　Splay树，又叫伸展树，可以实现快速分裂合并一个序列，几乎可以完成平衡树的所有操作。其中最重要的操作是将指定节点伸展到指定位置，

　　目录

  1. 节点定义
  2. 旋转操作
  3. 伸展操作
  4. 插入操作
  5. 删除操作
  6. lower_bound&upper_bound
  7. 前驱后继操作
  8. 可重Splay
  9. 名次操作
  10. 区间操作

 

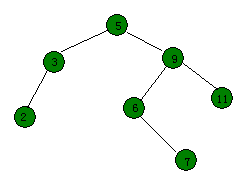
节点定义

　　一棵普通的splay并不需要什么太多的附加数据，就像下面这样就好:

 1 template<typename T>
 2 class SplayNode {
 3     public:
 4         T data;
 5         SplayNode* next[2];
 6         SplayNode* father;
 7         SplayNode(){
 8             memset(next, 0, sizeof(next));
 9         }
10         SplayNode(T data, SplayNode* father):data(data), father(father){
11             memset(next, 0, sizeof(next));
12         }
13         int cmp(T a){
14             if(a == data)    return -1;
15             return (a > data) ? (1) : (0);
16         }
17 };

伸展操作

 　　伸展操作有三种情况，分为单旋转（一种情况）和双旋转（二种情况）

  1. 当伸展的节点的父节点为目标位置，那么只需要一次旋转就可以完成。和这个方向相反（如果为左子树，就右旋）
    例如将开篇那张图中键值为3的点，伸展到根。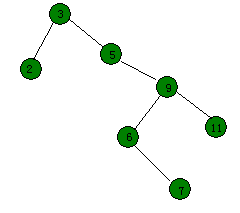

  2. 要伸展的节点的父节点和祖父节点共线，则先将父节点转上去，再将该节点转上去，例如上图，将键值为9的节点伸展到根。
  3. 第三种情况是要伸展的节点的父节点和祖父节点不共线（呈"之"字），此时先将该节点连续旋转两次达到祖父节点的位置。例如将第一张图的键值为6的节点伸展到根。

 　　基本所有题目的数据范围都不至于使一次单旋转或双旋转就能够解决，所以实际中是通过三种情况组合进行伸展。

　　比如说将某个深度较深的节点伸展到根，会发现不光是这个节点的深度更小了（更浅），很多其它节点也有所受益。最坏的情况是O（n）（从小到大的数据中最小的一个伸展到根），最好的情况O（1）（刚好是父节点的直接的某个子树），平均是O（log2n）(我也不知道怎么算的，反正实际用起来绝对比这个慢，或者说常数很大，因为Splay不像AVL树和红黑树那样特别平衡)。

　　您可以考虑在插入、查找的过程中把结果伸展到根。

　　下面是代码:

 1 inline void splay(SplayNode<T>* node, SplayNode<T>* father){
 2     while(node->father != father){
 3         SplayNode<T>* f = node->father;
 4         int fd = f->cmp(node->data);
 5         SplayNode<T>* ff = f->father;
 6         if(ff == father){
 7             rotate(f, fd ^ 1);
 8             break;
 9         }
10         int ffd = ff->cmp(f->data);
11         if(ffd == fd){
12             rotate(ff, ffd ^ 1);
13             rotate(f, fd ^ 1);
14         }else{
15             rotate(f, fd ^ 1);
16             rotate(ff, ffd ^ 1);
17         }
18     }
19     if(father == NULL)
20         root = node;
21 }

插入操作

　　Splay的插入操作很简单，按照BST的性质插进去，然后伸展到根。

 1 //实际过程
 2 static SplayNode<T>* insert(SplayNode<T>*& node, SplayNode<T>* father, T data){
 3     if(node == NULL){
 4         node = new SplayNode<T>(data, father);
 5         return node;
 6     }
 7     int d = node->cmp(data);
 8     if(d == -1)    return NULL;
 9     return insert(node->next[d], node, data);
10 }
11 
12 //用户调用
13 inline SplayNode<T>* insert(T data){
14     SplayNode<T>* res = insert(root, NULL, data);
15     if(res != NULL)    splay(res, NULL);
16     return res;
17 }

 

删除操作

　　虽然Treap的删除貌似在这也可以借鉴一下，但是还是希望用到splay函数。

　　比如开始那张图，要删除键值为7的节点，那么先把它伸展到根:

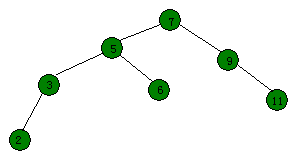
　　如果某棵子树为空，那么直接删掉就好了，然后改下root。

　　先假设键值为6的节点不存在，那么直接用键值为5的节点来代替根节点就好了。可是事实上有键值为6的节点。那么想一种情况根节点的左子树的右子树为空的情况。很巧根据BST的性质（设根节点为x，根节点的左子树为y，y的右子树为z），那么x > z > y。如果不存在z，也就是说y是x的前驱（小于x且最大的数）。

 　　根据前驱的定义，可以写出一下找根节点的前驱的代码。

SplayNode<T>* maxi = re->next[0];
while(maxi->next[1] != NULL) maxi = maxi->next[1];

　　找到前驱然后伸展到根节点的左子树。最后的结果图:

　　实际应用时通常会加入永远都不可能被删掉的最小的一个节点（哨兵节点），这样根就不存在要删的节点的左子树为空的情况。所以可以省下一些代码。

代码:

 1 inline boolean remove(T data){
 2             SplayNode<T>* re = find(data);
 3             if(re == NULL)    return false;
 4             SplayNode<T>* maxi = re->next[0];
 5             if(maxi == NULL){
 6                 root = re->next[1];
 7                 if(re->next[1] != NULL)    re->next[1]->father = NULL;
 8                 delete re;
 9                 return true;
10             }
11             while(maxi->next[1] != NULL) maxi = maxi->next[1];
12             splay(maxi, re);
13             maxi->next[1] = re->next[1];
14             if(re->next[1] != NULL)    re->next[1]->father = maxi;
15             maxi->father = NULL;
16             delete re;
17             root = maxi;
18             return true;
19         }

 

前驱后继操作

　　首先把要求前驱或后继的节点伸展到根。然后很容易就想到。

 1 inline SplayNode<T>* findPre(SplayNode<T>* node) {
 2     if(node != root)    splay(node, NULL);
 3     SplayNode<T>* s = node->next[0];
 4     while(s != NULL && s->next[1] != NULL)    s = s->next[1];
 5     return s;
 6 }
 7         
 8 inline SplayNode<T>* findSuf(SplayNode<T>* node) {
 9     if(node != root)    splay(node, NULL);
10     SplayNode<T>* s = node->next[1];
11     while(s != NULL && s->next[0] != NULL)    s = s->next[0];
12     return s;
13 }

　　如果不是该树内的节点，后继用upper_bound,前驱就用自创的less_bound。思路和upper_bound差不多。

 1 static SplayNode<T>* less_bound(SplayNode<T>*& node, T val){
 2     if(node == NULL)    return node;
 3     int to = node->cmp(val);
 4     if(val == node->data)    to = 0;
 5     SplayNode<T>* ret = less_bound(node->next[to], val);
 6     return (ret == NULL && node->data < val) ? (node) : (ret);
 7 }
 8 
 9 SplayNode<T>* less_bound(T data){
10     SplayNode<T>* p = less_bound(root, data);
11     if(p != NULL)
12         splay(p, NULL);
13     return p;
14 }

可重Splay

·节点定义

　　既然让Splay支持重复的内容，那么就要加入一个count。因为根据BST的性质，新加入的重复的节点，放哪都会破坏性质（因为都是大于或小于），所以只好加在原先节点的头上

 1 template<typename T>
 2 class SplayNode {
 3     public:
 4         T data;
 5         int count;                          //这里
 6         SplayNode* next[2];
 7         SplayNode* father;
 8         SplayNode(){ 
 9             memset(next, 0, sizeof(next));
10         }
11         SplayNode(T data, SplayNode* father):data(data), father(father), count(1){
12             memset(next, 0, sizeof(next));
13         }
14         int cmp(T a){
15             if(a == data)    return -1;
16             return (a > data) ? (1) : (0);
17         }
18         void addCount(int val){      //这里
19             this->count += val;
20         }
21 };

·插入 & 删除操作

　　插入特判是否有重复的键值，删除特判count为0.(即是否需要移除节点)

名次操作

　　要进行名次操作（K小值和x的排名）对于一个节点，要做到O（log2n） 就要想办法通过某些手段不做一些无用的访问。这时可以考虑加入一个s（size）附加数据，记录该子树上的节点（数据，包括重复的内容）个数。

　　而且旋转后某些节点的s需要改变，所以需要一个维护s的函数

 1 template<typename T>
 2 class SplayNode {
 3     public:
 4         T data;
 5         int s;                                //这里
 6         int count;
 7         SplayNode* next[2];
 8         SplayNode* father;
 9         //.......
10         void maintain(){                //这里
11             s = count;
12             for(int i = 0; i < 2; i++)
13                 if(next[i] != NULL)
14                     s += next[i]->s;
15         }
16         void addCount(int val){
17             this->s += val;
18             this->count += val;        //这里
19         }
20 };

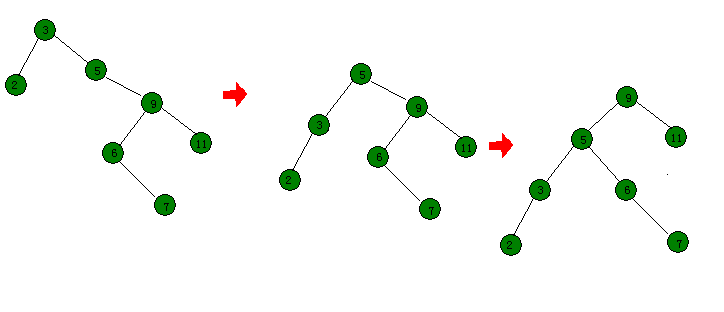
　　旋转时，如何确定待维护节点？先看一下下图（怎么感觉两张图都有在树链剖分）

　　由此可以得出规律，旧的"根节点"和新的"根节点"需要维护。

1 inline static void rotate(SplayNode<T>*& node, int d){
2     //.......
3     node->maintain();
4     node->father->maintain();
5 }
6

　　首先来说求K小值吧，从根节点开始访问(这不是废话吗)，然后确定左子树的个数ls，如果左子树为空，那么就记为0。

　　很容易就能想到一个节点的左子树的个数为ls个，那么以这个节点为根的树上，根的排名是(ls + 1)名。于是我们可以得出递归的边界（写成while也行）

if(k >= ls + 1 && k <= ls + node->count)    return node;

　　如果访问左子树（k <= ls），那么没有什么特别的。但是如果访问右子树，你现在要求的右子树上的第某小值，而k是对于当前的node来说，所以应该减去s和node->count。

　　K小值代码:

 1 static SplayNode<T>* findKth(SplayNode<T>*& node, int k){
 2     int ls = (node->next[0] != NULL) ? (node->next[0]->s) : (0);
 3     if(k >= ls + 1 && k <= ls + node->count)    return node;
 4     if(k <= ls)    return findKth(node->next[0], k);
 5     return findKth(node->next[1], k - ls - node->count);
 6 }
 7 
 8 inline SplayNode<T>* findKth(int k){
 9     if(k <= 0 || k > root->s)    return NULL;
10     SplayNode<T>* p = findKth(root, k);
11     splay(p, NULL);
12     return p;
13 }

　　求x的排名就很简单了。还是访问，比当前节点小，访问左子树，相等返回r + 1，否则访问右子树,r加上当前节点的左子树的大小和count。如果访问到了NULL，返回r + 1。

　　为什么返回的都是r + 1呢？

　　因为加的左子树的大小等都是确定比它小的节点的个数。

下面是代码:

 1 inline int rank(T data){
 2     SplayNode<T>* p = root;
 3     int r = 0;
 4     while(p != NULL){
 5         int ls = (p->next[0] != NULL) ? (p->next[0]->s) : (0);
 6         if(p->data == data)    return r + ls + 1;
 7         int d = p->cmp(data);
 8         if(d == 1)    r += ls + p->count;
 9         p = p->next[d];
10     }
11     return r + 1;
12 }

区间操作

·split(int from, int end)

　　从原树中分离出一段区间[from, end]。

　　和之前删除的思想一样，调用splay函数使某个（没错，就是一个）特定的子树就是这一个区间。这里不好想，我就直接说吧。

 1 /*
 2 *    先找到第(end + 1)名，然后伸展到根，然后找到(from - 1)名，伸展到根的左子树。然后根的左子树的右子树就是这个区间了。
 3 *    当然(end + 1)和(from - 1)都不一定会存在，所以特判或者加入哨兵节点。
 4 */
 5 SplayNode<T>* split(int from, int end){
 6     if(from > end)    return NULL;
 7     if(from == 1 && end == root->s){
 8         findKth(1, NULL);
 9         return this->root;
10     }
11     if(from == 1){
12         findKth(end + 1, NULL);
13         findKth(from, root);
14         return root->next[0];
15     }
16     if(end == root->s){
17         findKth(from - 1, NULL);
18         findKth(end, root);
19         return root->next[1];
20     }
21     findKth(end + 1, NULL);
22     findKth(from - 1, root);
23     return root->next[0]->next[1];
24 }
分离区间

　　不过通常都需要用Splay来处理字符串等，这些是按照数组下标来建立Splay。翻转也是家常便饭，因此只能靠访问的顺序来当成"下标"（翻转后很难修改记录的下标）。

　　至于翻转操作就打lazy标记，然后建立一个pushDown()函数

1 void pushDown(){
2     swap(next[0], next[1]);
3     for(int i = 0; i < 2; i++)
4         if(next[i] != NULL)
5             next[i]->lazy ^= 1;
6     lazy = false;
7 }

　　就像这样，很多区间操作都可以做。

posted @ 2017-01-15 10:41  阿波罗2003  阅读(594)  评论(0)  编辑  收藏  举报