[数据结构]Treap简介

[写在前面的话]

　　如果想学Treap，请先了解BST和BST的旋转

二叉搜索树（BST）（百度百科）:[here]

英文好的读者可以戳这里(维基百科)

自己的博客:关于旋转（很水，顶多就算是了解怎么旋转，建议自行上百度）[here]

　　Treap(= binary search Tree + Heap)，中文通常译作树堆，为每个节点附加一个优先值，让优先值满足堆的性质，防止BST退化成一条链。

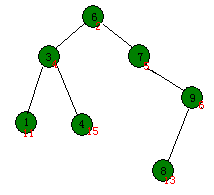
[节点定义]

　　每个节点像下面这样定义:

 1 template<typename T>
 2 class TreapNode{
 3     public:
 4         T data;        //数据 
 5         int r;        //（随机）优先级，用于满足堆的性质，防止退化成链 
 6         TreapNode* next[2];        //两颗子树，0为左子树，1为右子树 
 7         TreapNode* father;        //父节点，可选 
 8         TreapNode(T data, int r, TreapNode* father):data(data), r(r), father(father){
 9             memset(next, 0, sizeof(next));
10         }
11         inline int cmp(T d){    //比较函数 
12             if(d > data)    return 1;
13             return 0;
14         }
15 };

[旋转操作]

　　如果像之前那张博客那样打旋转操作，那么到Splay的伸展函数的时候只能笑了。

1 static void rotate(TreapNode<T>*& node, int d){
2     TreapNode<T>* newRoot = node->next[d ^ 1];
3     newRoot->father = node->father;
4     node->next[d ^ 1] = newRoot->next[d];
5     node->father = newRoot;
6     newRoot->next[d] = node;
7     if(node->next[d ^ 1] != NULL)    node->next[d ^ 1]->father = node;
8     if(newRoot->father != NULL)    newRoot->father->next[newRoot->father->cmp(newRoot->data)] = newRoot; 
9 }

　　这里用d来表示旋转的方向。这样就不至于在旋转的时候后需要用一次if else

　　其实这里的father可以说用不到，只不过删除操作的时候需要把查找加到一起。

[插入操作]

　　插入操作时首先按照BST的插入方式进行插入，然后很快就会发现破坏了Heap的性质，比如说上面那张图插入了一个键值为10，优先级为4的节点，按照这个方法，会形成下图这种情形:

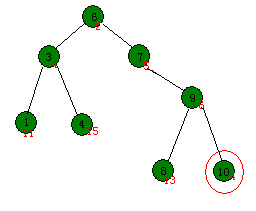
　　新插入的节点破坏了Heap的性质，那么只能同一种只会改变节点的位置，却不破坏BST的性质的方法来维护——旋转。

　　为了不制造更多的麻烦（就是通过旋转使其他节点破坏堆的性质），所以应该比父节点更小的那个节点以相反的方向（“有问题的节点”是它的右子树则左旋，否则右旋）旋转到“当前位置”。如下图:

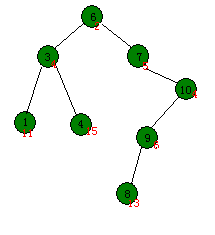
　　最后经过调整，它满足了堆的性质:

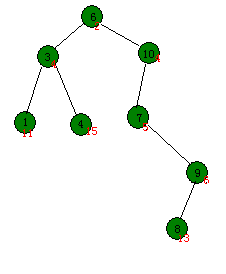
　　下面是关于插入的完整代码:

 1 //实际过程
 2 static boolean insert(TreapNode<T>*& node, TreapNode<T>* father, T data, int d){
 3     if(node == NULL){
 4         node = new TreapNode<T>(data, rand(), father);
 5         if(father != NULL)    father->next[d] = node;
 6         return true;
 7     }
 8     int d1 = node->cmp(data);
 9     if(node->data == data)    return false;
10     boolean res = insert(node->next[d1], node, data, d1);
11     if(node->next[d1]->r > node->r){
12         rotate(node, d1 ^ 1);
13     }
14     return res;
15 }
16 
17 //用户调用
18 boolean insert(T& data){
19     boolean res = insert(root, NULL, data, 0);
20     while(root->father != NULL)    root = root->father;
21     return res;
22 }

[查找操作]

　　查找就根据BST的性质进行二分查找就可以了。

 1 //实际过程
 2 static TreapNode<T>* find(TreapNode<T>*& node, T data){
 3     if(node == NULL    || node->data == data)    return node;
 4     return find(node->next[node->cmp(data)], data);
 5 }
 6 
 7 //用户调用
 8 TreapNode<T>* find(T data){
 9     return find(root, data);
10 }
11 
12 boolean count(T data){
13     return (find(root, data) != NULL);
14 }

[删除操作]

　　Treap的删除首先是要找到这个节点。可以试试下面这种情况（删除键值为3的节点）:

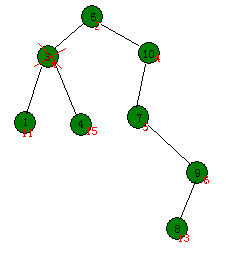
　　是不是看着怪怪的？那换个简单的，就把键值为9的节点删掉，维护很简单，直接用它唯一的子树来代替它的位置。

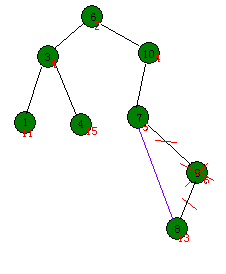
　　那么再来思考刚刚的问题，删掉键值为3的节点。既然当要删的节点只有一棵子树（或者没有子树）时特别简单，那么反正这个节点也是要删的，暂时破坏一下堆的性质，把它旋转到能够使它只有一个子树的时候，再把它删掉。为了不制造更多的麻烦（就在旋转时，让除去这个节点其他的节点破坏堆的性质），所以应该把更小的那一个子树旋转上来。如下图:

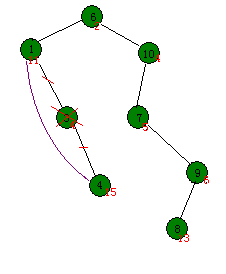
　　下面是删除操作的代码。

 1 //实际过程
 2 static void remove(TreapNode<T>*& node, TreapNode<T>*& root){
 3     int direc = ((node->father != NULL) ? (node->father->cmp(node->data)) : (-1));
 4     if(node->next[0] == NULL && node->next[1] == NULL){
 5         if(direc != -1)    node->father->next[direc] = NULL;
 6         else root = NULL;
 7         delete node;
 8     }else if(node->next[0] == NULL || node->next[1] == NULL){
 9         TreapNode<T>* stick = (node->next[0] == NULL) ? (node->next[1]) : (node->next[0]);
10         if(direc == -1){
11             root = stick;
12             stick->father = NULL;
13         }else{
14             node->father->next[direc] = stick;
15             stick->father = node->father;
16         }
17         delete node;
18     }else{
19         if(node->next[0]->r < node->next[1]->r)    rotate(node, 1);
20         else rotate(node, 0);
21         while(root->father != NULL)    root = root->father;
22         remove(node, root);
23     }
24 }
25 
26 //用户调用
27 boolean remove(T data){
28     TreapNode<T>* node = find(data);
29     if(node == NULL)    return false;
30     remove(node, root);
31     return true;
32 }

　　这个代码真的写得不简洁，但是还是要注意下面这几个事项:

删除要改变父节点还有子节点的指针
旋转的方向
记得释放节点占用的内存(如果不是单个文件多组数据输入，其实一般也不会超内存)

[其它操作]

·lower_bound(T data)

　　还是来看刚刚那棵树，这次我们执行lower_bound(5)，很明显，这里结果是6。

首先从根节点开始访问（这不是废话吗），如果遇到相等的或者NULL就可以return了(这有用吗？)

　　仍然按照和查找一样的方法，以找到和它一样的节点为目标，于是可以得到了如下访问顺序

6 3 4 NULL

　　看起来被迫得返回了。在返回的过程中，找到的第一个大于它的就是结果，否则不存在。于是得到了6。

　　下面是代码(至少我认为这个代码还算比较简洁的。。):

 1 //实际过程
 2 static TreapNode<T>* lower_bound(TreapNode<T>*& node, T val){
 3     if(node == NULL || node->data == val)    return node;
 4     int to = node->cmp(val);
 5     TreapNode<T>* ret = lower_bound(node->next[to], val);
 6     return (ret == NULL && node->data > val) ? (node) : (ret);
 7 }
 8 
 9 //用户调用
10 TreapNode<T>* lower_bound(T data){
11     return lower_bound(root, data);
12 }

·upper_bound(T data)

　　upper_bound和lower_bound差不多，只不过在相等的时候是访问右子树。其它的都是一样的

 1 //实际过程
 2 static TreapNode<T>* upper_bound(TreapNode<T>*& node, T val){
 3     if(node == NULL)    return node;
 4     int to = node->cmp(val);
 5     if(val == node->data)    to = 1;
 6     TreapNode<T>* ret = upper_bound(node->next[to], val);
 7     return (ret == NULL && node->data > val) ? (node) : (ret);
 8 }
 9 
10 //用户调用
11 TreapNode<T>* upper_bound(T data){
12     return upper_bound(root, data);
13 }

[完整代码]

  1 #include<iostream>
  2 #include<fstream>
  3 #include<sstream>
  4 #include<cstdio>
  5 #include<cstdlib>
  6 #include<cstring>
  7 #include<ctime>
  8 #include<cctype>
  9 #include<cmath>
 10 #include<algorithm>
 11 #include<stack>
 12 #include<queue>
 13 #include<set>
 14 #include<map>
 15 #include<vector>
 16 using namespace std;
 17 typedef bool boolean;
 18 #define smin(a, b)    (a) = min((a), (b))
 19 #define smax(a, b)    (a) = max((a), (b))
 20 template<typename T>
 21 inline void readInteger(T& u){
 22     char x;
 23     int aFlag = 1;
 24     while(!isdigit((x = getchar())) && x != -1);
 25     if(x == -1){
 26         x = getchar();
 27         aFlag = -1;
 28     }
 29     for(u = x - '0'; isdigit((x = getchar())); u = (u << 3) + (u << 1) + x - '0');
 30     ungetc(x, stdin);
 31     u *= aFlag;
 32 }
 33 
 34 template<typename T>
 35 class TreapNode{
 36     public:
 37         T data;
 38         int r;
 39         TreapNode* next[2];
 40         TreapNode* father;
 41         TreapNode(T data, int r, TreapNode* father):data(data), r(r), father(father){
 42             memset(next, 0, sizeof(next));
 43         }
 44         inline int cmp(T d){
 45             if(d > data)    return 1;
 46             return 0;
 47         }
 48 };
 49 
 50 template<typename T>
 51 class Treap{
 52     protected:
 53         static boolean insert(TreapNode<T>*& node, TreapNode<T>* father, T data, int d){
 54             if(node == NULL){
 55                 node = new TreapNode<T>(data, rand(), father);
 56                 if(father != NULL)    father->next[d] = node;
 57                 return true;
 58             }
 59             int d1 = node->cmp(data);
 60             if(node->data == data)    return false;
 61             boolean res = insert(node->next[d1], node, data, d1);
 62             if(node->next[d1]->r > node->r){
 63                 rotate(node, d1 ^ 1);
 64             }
 65             return res;
 66         }
 67         
 68         static TreapNode<T>* find(TreapNode<T>*& node, T data){
 69             if(node == NULL    || node->data == data)    return node;
 70             return find(node->next[node->cmp(data)], data);
 71         }
 72         
 73         static void remove(TreapNode<T>*& node, TreapNode<T>*& root){
 74             int direc = ((node->father != NULL) ? (node->father->cmp(node->data)) : (-1));
 75             if(node->next[0] == NULL && node->next[1] == NULL){
 76                 if(direc != -1)    node->father->next[direc] = NULL;
 77                 else root = NULL;
 78                 delete node;
 79             }else if(node->next[0] == NULL || node->next[1] == NULL){
 80                 TreapNode<T>* stick = (node->next[0] == NULL) ? (node->next[1]) : (node->next[0]);
 81                 if(direc == -1){
 82                     root = stick;
 83                     stick->father = NULL;
 84                 }else{
 85                     node->father->next[direc] = stick;
 86                     stick->father = node->father;
 87                 }
 88                 delete node;
 89             }else{
 90                 if(node->next[0]->r < node->next[1]->r)    rotate(node, 1);
 91                 else rotate(node, 0);
 92                 while(root->father != NULL)    root = root->father;
 93                 remove(node, root);
 94             }
 95         }
 96         
 97         static TreapNode<T>* lower_bound(TreapNode<T>*& node, T val){
 98             if(node == NULL || node->data == val)    return node;
 99             int to = node->cmp(val);
100             TreapNode<T>* ret = lower_bound(node->next[to], val);
101             return (ret == NULL && node->data > val) ? (node) : (ret);
102         }
103         
104         static TreapNode<T>* upper_bound(TreapNode<T>*& node, T val){
105             if(node == NULL)    return node;
106             int to = node->cmp(val);
107             if(val == node->data)    to = 1;
108             TreapNode<T>* ret = upper_bound(node->next[to], val);
109             return (ret == NULL && node->data > val) ? (node) : (ret);
110         }
111         
112     public:
113         TreapNode<T> *root;
114         
115         boolean insert(T& data){
116             boolean res = insert(root, NULL, data, 0);
117             while(root->father != NULL)    root = root->father;
118             return res;
119         }
120         
121         TreapNode<T>* find(T data){
122             return find(root, data);
123         }
124         
125         boolean count(T data){
126             return (find(root, data) != NULL);
127         }        
128         
129         boolean remove(T data){
130             TreapNode<T>* node = find(data);
131             if(node == NULL)    return false;
132             remove(node, root);
133             return true;
134         }
135         
136         TreapNode<T>* lower_bound(T data){
137             return lower_bound(root, data);
138         }
139         
140         TreapNode<T>* upper_bound(T data){
141             return upper_bound(root, data);
142         }
143         
144         static void rotate(TreapNode<T>*& node, int d){
145             TreapNode<T>* newRoot = node->next[d ^ 1];
146             newRoot->father = node->father;
147             node->next[d ^ 1] = newRoot->next[d];
148             node->father = newRoot;
149             newRoot->next[d] = node;
150             if(node->next[d ^ 1] != NULL)    node->next[d ^ 1]->father = node;
151             if(newRoot->father != NULL)    newRoot->father->next[newRoot->father->cmp(newRoot->data)] = newRoot; 
152         }
153         
154         //调试用函数 
155         void out(TreapNode<T>* node){
156             if(node == NULL)    return;
157             out(node->next[0]);
158             printf("%d ", node->data);
159             out(node->next[1]);
160         }
161         
162 };
163 
164 Treap<int> t;
165 int main(){
166     srand((unsigned)time(NULL));
167     freopen("treap.in", "r", stdin);
168     freopen("treap.out", "w", stdout);
169     int n;
170     readInteger(n);
171     for(int i = 1, a; i <= n; i++){
172         getchar();
173         char op = getchar();
174         readInteger(a);
175         if(op == 'I'){
176             boolean aFlag = t.insert(a);
177             if(aFlag)    printf("S\n");
178             else printf("F\n");
179         }else if(op == 'D'){
180             boolean aFlag = t.remove(a);
181             if(aFlag)    printf("S\n");
182             else printf("F\n");
183         }else if(op == 'L'){
184             TreapNode<int>* d = t.lower_bound(a);
185             if(d == NULL)    printf("NONE\n");
186             else printf("%d\n", d->data);
187         }else{
188             TreapNode<int>* d = t.upper_bound(a);
189             if(d == NULL)    printf("NONE\n");
190             else printf("%d\n", d->data);
191         }
192     }
193 //    t.out(t.root);
194     return 0;
195 }

Treap

[后记]

　　可以用这份代码和STL的set比比速度，反正在我的电脑上插入、删除都比set快，只有lower_bound和upper_bound稍微比set慢一些。

只不过如果Treap只是做这些的话，直接用set就好了。

　　于是有了基于普通Treap的数据结构

名次树_{(当然，也可以用其它平衡树实现)}	为Treap的节点附加一个s来统计该子树上的节点总数，然后旋转、插入、删除的时候维护，就可以来求k小值，和某个数的排名
可持久化Treap	实现可快速分裂合并的序列时，无论是代码量还是速度，都轻松秒杀Splay

　　提供测试数据和题目[here]

posted @ 2017-01-14 09:28 阿波罗2003 阅读(767) 评论(0) 编辑收藏举报

刷新页面返回顶部