[算法]树上倍增求LCA
LCA指的是最近公共祖先(Least Common Ancestors),如下图所示:
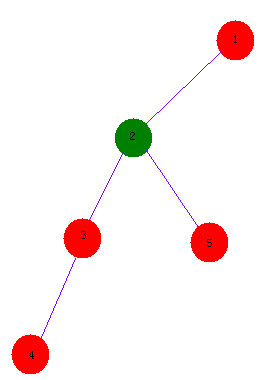
4和5的LCA就是2
那怎么求呢?最粗暴的方法就是先dfs一次,处理出每个点的深度
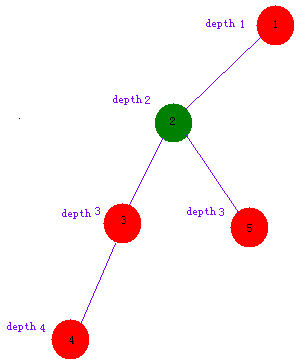
然后把深度更深的那一个点(4)一个点地一个点地往上跳,直到到某个点(3)和另外那个点(5)的深度一样
然后两个点一起一个点地一个点地往上跳,直到到某个点(就是最近公共祖先)两个点“变”成了一个点
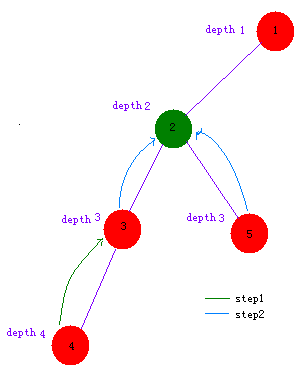
不过有没有发现一个点地一个点地跳很浪费时间?
如果一下子跳到目标点内存又可能不支持,相对来说倍增的性价比算是很高的
倍增的话就是一次跳2i 个点,不难发现深度差为x时,深度更深的那个点就需要跳x个点
于是可以写出这段代码
1 if(depth[a] < depth[b]) swap(a, b); 2 int c = depth[a] - depth[b]; 3 for(int i = 0; i <= 14; i++){ 4 if(c & (1 << i)){ 5 a = up[a][i]; 6 } 7 }
接下来很快就会发现一个很严重的问题:两个点按照这样跳,不能保证一定是最近的
所以倍增找lca的方法是这样的:
从最大可以跳的步数开始跳(一定是2i),如果跳的到的位置一样,就不跳,如果不一样才跳,每次跳的路程是前一次的一半
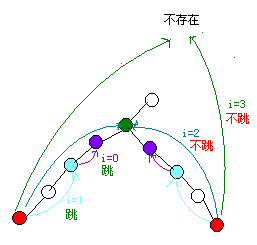
过程大概就像上图所示,但是执行完了这一段到的点不是最近公共祖先,但是,它们再往上跳一格,就到了
把这一段写成代码,就成了这样:
1 for(int i = 14; i >= 0; i--){ 2 if(up[a][i] != up[b][i]){ 3 a = up[a][i]; 4 b = up[b][i]; 5 } 6 }
前面还需要加上一句特判(当a和b在同一边时,深度浅的那个点就是最近公共祖先)
if(a == b) return a;
好了,会求lca了,关键是怎么构造倍增数组。
没有疑问的是向上跳一格就是自己的父节点
f[i][0] = fa[i];
这个是初值,接着可以根据这个推出来其他的,除此之外还要附上初值0,不然有可能会RE
f[i][j] = f[f[i][j - 1]][j - 1];
就是把这一段路,分成两段已经知道的
完整代码就是这样的:
1 Matrix<int> up; 2 inline void init_bz(){ 3 up = Matrix<int>(16, n + 1); 4 memset(up.p, 0, sizeof(int) * 16 * (n + 1)); 5 for(int i = 1; i <= n; i++){ 6 up[i][0] = fa[i]; 7 } 8 for(int j = 1; j <= 14; j++){ 9 for(int i = 1; i <= n; i++){ 10 up[i][j] = up[up[i][j - 1]][j - 1]; 11 } 12 } 13 }
注意倍增求LCA适用于询问多的情况,不然光在预处理上花的时间就已经够多了(如果只有一两个询问,直接暴力就好了)
当然,这个倍增算法判断条件是若干级祖先是否相等。
同样,点$u$,$v$的LCA还满足它是其中一个点的最近的一个祖先,满足$u$,$v$都在它的子树中。
判断一个点是否在另一个点的子树中,我们可以用dfs序来判断。
这是倍增的另一种判断方法:
1 void dfs(int p, int fa) { 2 bz[p][0] = fa, in[p] = ++cnt; 3 for (int i = 1; i < bzmax; i++) 4 bz[p][i] = bz[bz[p][i - 1]][i - 1]; 5 for (int i = g.h[p]; ~i; i = g[i].nx) { 6 int e = g[i].ed; 7 if (e == fa) continue; 8 dfs(e, p); 9 } 10 out[p] = cnt; 11 } 12 13 int lca(int a, int b) { 14 if (dep[a] > dep[b]) swap(a, b); 15 if (in[a] <= in[b] && out[a] >= out[b]) 16 return a; 17 for (int i = bzmax - 1, nx; ~i; i--) { 18 nx = bz[a][i]; 19 if (!(in[nx] <= in[b] && out[nx] >= out[b])) 20 a = nx; 21 } 22 return bz[a][0]; 23 } 24
