Java实现Tire
Trie,又称单词查找树或键树,是一种树形结构。典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:最大限度地减少无谓的字符串比较,查询效率比哈希表高。
它有3个基本性质:
- 根节点不包含字符,除根节点外每一个节点都只包含一个字符。
- 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
- 每个节点的所有子节点包含的字符都不相同。
下面这个图就是Trie的表示,每一条边表示一个字符,如果结束,就用星号表示。在这个Trie结构里,我们有下面字符串,比如do, dork, dorm等,但是Trie里没有ba, 也没有sen,因为在a, 和n结尾,没有结束符号(星号)。
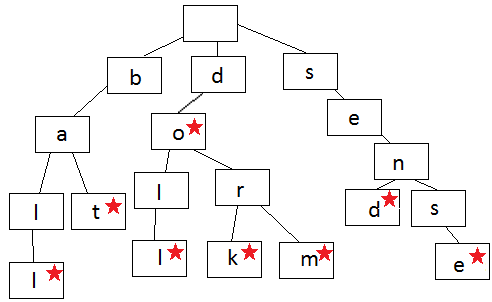
有了这样一种数据结构,我们可以用它来保存一个字典,要查询改字典里是否有相应的词,是否非常的方便呢?我们也可以做智能提示,我们把用户已经搜索的词存在Trie里,每当用户输入一个词的时候,我们可以自动提示,比如当用户输入 ba, 我们会自动提示 bat 和 baii.
现在来讨论Trie的实现。
首先,我们定义一个Abstract Trie,Trie 里存放的是一个Node。这个类里有两个操作,一个是插入,另一个是查询。具体实现放在后面。
实现
Node类:
package com.yydcdut; import java.util.LinkedList; public class Node { char content; //装node中的内容 boolean isEnd; //是否是单词的结尾 int count; //这个单词的这个字母下面分支的个数 LinkedList<Node> childList; //子list /** * 构造函数 * @param c 单词的字母 */ public Node(char c){ childList = new LinkedList<Node>(); isEnd = false; content = c; count = 0; } /** * 遍历一下这个node中LinkedList中是否有这个字母,有就意味着可以继续查找下去,没有就没有。 * @param c 单词的字母 * @return 如果有的话就返回下一个node,没有的话就返回null */ public Node subNode(char c){ if(childList != null){ for(Node eachChild : childList){ if(eachChild.content == c){ return eachChild; } } } return null; } }
具体实现:
package com.yydcdut; public class Main { private Node root; //根 /** * 构造函数,生成根 */ public Main(){ root = new Node(' '); } /** * 插入函数,先判断是否有这个单词了(通过每个单词字母来判断),如果没有,挨着顺序判断是否有这个字母了, *如果有这个字幕,继续判断下一个,当没有这个字母的时候,对这个字母new一个node对象,放入到上一个字母的 *LinkedList里面 * @param word 要插入的单词 */ public void insert(String word){ //如果找到就返回 if(search(word) == true) return; Node current = root; for(int i = 0; i < word.length(); i++){ Node child = current.subNode(word.charAt(i)); if(child != null){ current = child; } else { current.childList.add(new Node(word.charAt(i))); current = current.subNode(word.charAt(i)); } //单词下面分支数++ current.count++; } //在单词最后字母那里结束了 current.isEnd = true; } /** * 查找函数,判断是否已经有隔着单词了 * @param word 要判断的单词 * @return 有这个单词返回true,没有返回false */ public boolean search(String word){ Node current = root; for(int i = 0; i < word.length(); i++){ if(current.subNode(word.charAt(i)) == null) return false; else current = current.subNode(word.charAt(i)); } //判断这个单词的这个字母是否在字典里面结束了 if (current.isEnd == true) return true; else return false; } /** * 删除函数,先判断是否存在这个单词,不存在就跳出,存在就删除掉,每个单词的count都要减1 * @param word 要删除的单词 */ public void deleteWord(String word){ if(search(word) == false) return; Node current = root; for(char c : word.toCharArray()) { Node child = current.subNode(c); if(child.count == 1) { current.childList.remove(child); return; } else { child.count--; current = child; } } current.isEnd = false; } public static void main(String[] args) { Main trie = new Main(); trie.insert("ball"); trie.insert("balls"); trie.insert("sense"); System.out.println(trie.search("balls")); System.out.println(trie.search("ba")); trie.deleteWord("balls"); System.out.println(trie.search("balls")); System.out.println(trie.search("ball")); } }
时间复杂度分析:
对于insert, 如果被插入的String长度是 k, 每对一个字符进行查询,我们最多在child linkedlist里面查询26次(最多26个字母),所以,复杂度为O(26*k) = O(k). 对于 search, 复杂度是一样的。
我是天王盖地虎的分割线
源代码:http://pan.baidu.com/s/1dD1Qx01
trie.zip
参考:http://blog.csdn.net/beiyeqingteng
出处:http://yydcdut.cnblogs.com/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。

 新博客地址
新博客地址
 浙公网安备 33010602011771号
浙公网安备 33010602011771号