判断数据是否服从某一分布（一）
一、使用图形对数据初步进行描述。
使用（直方图，经验分布图，与QQ图）描述数据的分布结构，预判分布。
1.常用直方图，适用于连续性数据。
hist(x),lines(density(x))
2.经验分布图，一般的总体分布。
ecdf(x) #生成x的向量
plot(x, ..., ylab="Fn(x)", verticals = FALSE)#将生成的向量用plot画图
二、使用添加理想曲线或者QQ图判断是否服从某一分布。
1.添加理想曲线。
如：
w <- (min(x)-2):(max(x)+2)#绘制理想曲线范围，覆盖住原自变量范围
lines(w, dnorm(w, mean(x), sd(x)), col = "red") #添加正态分布dentisy理想曲线
2.QQ图
qqnorm(y, ylim, main = "Normal Q-Q Plot",
xlab = "Theoretical Quantiles",
ylab = "Sample Quantiles", plot.it = TRUE,
datax = FALSE, ...)
qqline(y, datax = FALSE, ...)
qqplot(x, y, plot.it = TRUE, xlab = deparse(substitute(x)),
ylab = deparse(substitute(y)), ...) #其中x是第一列样品,y是第二列样品或者只有此列样品。
三、实例
例一
数据：
已知15位学生的体重（单位千克）
75.0 64.0 47.4 66.9 62.2 62.2 58.7 66.6 64.0 57.0 69.0 56.9 50.0 72.0 63.5
分析：
1.数据为连续型随机变量，因此函数为连续型函数，使用直方图。
w <- c(75.0, 64.0, 47.4, 66.9, 62.2, 62.2, 58.7, 63.5, 66.6, 64.0, 57.0, 69.0, 56.9, 50.0, 72.0)
hist(w, freq = FALSE)
lines(density(w), col = "blue")
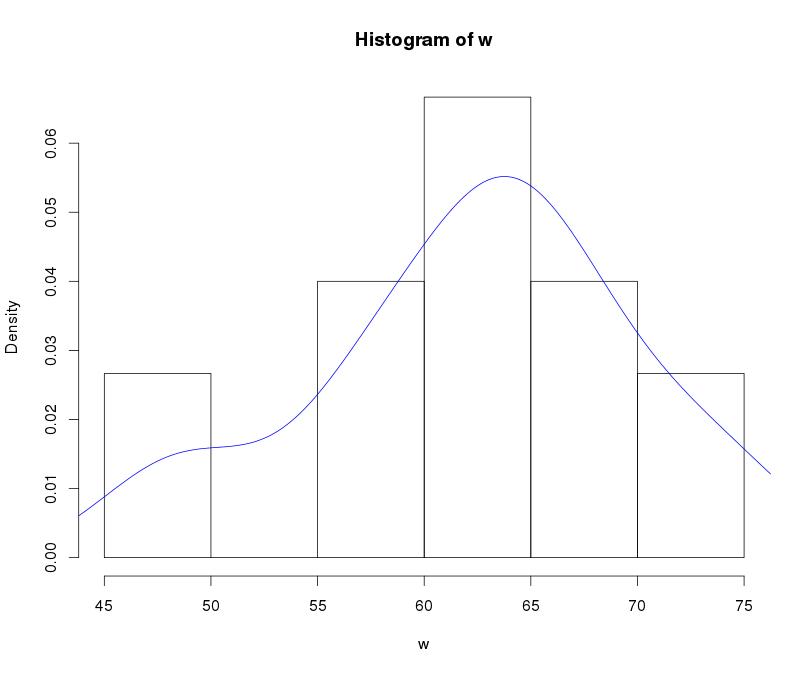
2.density图可看出类似正态分布，因此可以添加正态分布曲线进行观察，或者画QQ图判断是否服从正态分布。
2.1.可添加正态分布理想曲线进行观察。
x <- (min(w)-2):(max(w)+2)
lines(x, dnorm(x, mean(w), sd(w)), col = "red")
可观察到与正态分布曲线有一定区别，直方图偏右。
2.2.QQ图判断是否服从正态分布
qqnorm(w)
qqline(w)
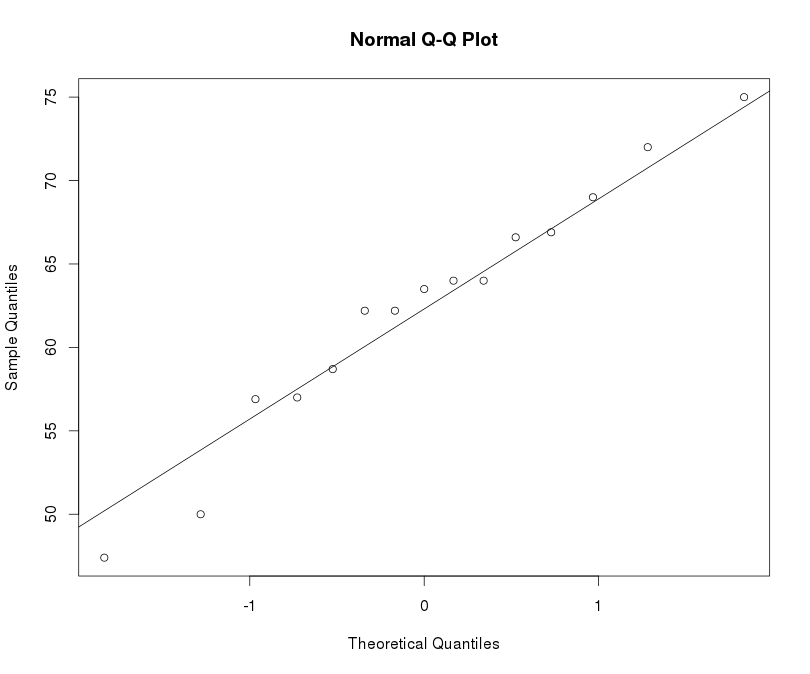
由QQ图可知样品的数据基本来自于正态分布。
例二
数据：
某公司接到一次电话的时间间隔，30个数据（单位：分钟）：
0.8 11.7 2.8 11.9 6.1 1
34.8 3.8 5.2 15.0 10.3 12.3
8.2 0.6 1.7 14.5 8.3 28.9
3.1 7.3 10.2 8.9 0.1 15.5
5.7 0.7 8.3 0.9 40.7 2.9
分析：
1.数据为连续型随机变量，因此函数为连续型函数，使用直方图。
x<-c( 0.8,11.7,2.8,11.9 ,6.1 ,1,
34.8 ,3.8,5.2,15.0,10.3,12.3,
8.2 ,0.6 ,1.7 ,14.5 , 8.3, 28.9,
3.1, 7.3 ,10.2 , 8.9 , 0.1 ,15.5,
5.7 ,0.7 , 8.3 , 0.9 ,40.7 , 2.9)
hist(x，freq=F)
lines(density(x),col="blue")
猜测为指数分布，再调节density曲线的adjust=2，两倍默认带宽，使曲线更加平滑。
hist(x,freq=F)
lines(density(x,adjust=2),col="blue")
2.density图可看出类似指数分布，因此可以添加指数分布曲线进行观察，或者画QQ图判断是否服从正态分布。
2.1.可添加指数分布理想曲线进行观察。
指数分布的λ的参数估计值为1/x拔。于是
λ <- 1/(mean(x))
t<- min(x):(max(x)+2)
lines(t,dexp(t,λ),col="red")
可知数据大致服从指数分布，但是不太理想。
2.2.QQ图判断是否服从指数分布
p <- ppoints(100) # 生成100个等距结点
q <- quantile(x,p=p) #生成样本分布的分位数
plot(qexp(p),q, main="Exponential Q-Q Plot",
xlab="Theoretical Quantiles",ylab="Sample Quantiles")
qqline(q, distribution=qexp,col="red", lty=2)
可以看出，前面大部分数据偏离直线不远，后面少部分数据偏离较远，数据大致服从指数分布。
