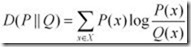KL距离，Kullback-Leibler Divergence

KL距离，是Kullback-Leibler差异（Kullback-Leibler Divergence）的简称，也叫做相对熵（Relative Entropy）。它衡量的是相同事件空间里的两个概率分布的差异情况。其物理意义是：在相同事件空间里，概率分布P(x)的事件空间，若用概率分布Q（x）编码时，平均每个基本事件（符号）编码长度增加了多少比特。我们用D（P||Q）表示KL距离，计算公式如下：

当两个概率分布完全相同时，即P(x)=Q(X)，其相对熵为0 。我们知道，概率分布P(X)的信息熵为：

其表示，概率分布P(x)编码时，平均每个基本事件（符号）至少需要多少比特编码。通过信息熵的学习，我们知道不存在其他比按照本身概率分布更好的编码方式了，所以D(P||Q）始终大于等于0的。虽然KL被称为距离，但是其不满足距离定义的三个条件：1）非负性；2）对称性（不满足）；3）三角不等式（不满足）。

我们以一个例子来说明，KL距离的含义。

假如一个字符发射器，随机发出0和1两种字符，真实发出概率分布为A，但实际不知道A的具体分布。现在通过观察，得到概率分布B与C。各个分布的具体情况如下：

A(0)=1/2，A(1)=1/2

B(0)=1/4，B(1)=3/4

C(0)=1/8，C(1)=7/8

那么，我们可以计算出得到如下：

也即，这两种方式来进行编码，其结果都使得平均编码长度增加了。我们也可以看出，按照概率分布B进行编码，要比按照C进行编码，平均每个符号增加的比特数目少。从分布上也可以看出，实际上B要比C更接近实际分布。

如果实际分布为C，而我们用A分布来编码这个字符发射器的每个字符，那么同样我们可以得到如下：

再次，我们进一步验证了这样的结论：对一个信息源编码，按照其本身的概率分布进行编码，每个字符的平均比特数目最少。这就是信息熵的概念，衡量了信息源本身的不确定性。另外，可以看出KL距离不满足对称性，即D(P||Q)不一定等于D(Q||P)。

当然，我们也可以验证KL距离不满足三角不等式条件。

上面的三个概率分布，D(B||C)=1/4log2+3/4log(6/7)。可以得到：D(A||C) - (D(A||B)+ D(B||C)) =1/2log2+1/4log(7/6)>0，这里验证了KL距离不满足三角不等式条件。所以KL距离，并不是一种距离度量方式，虽然它有这样的学名。

其实，KL距离在信息检索领域，以及统计自然语言方面有重要的运用。我们将会把它留在以后的章节中介绍。

其他相关链接：http://en.wikipedia.org/wiki/Kullback-Leibler_divergence

http://hi.baidu.com/shdren09/item/e6441ec2bd495b0e0ad93aca

利用信息论的方法可以进行一些简单的自然语言处理

比如利用相对熵进行分类或者是利用相对熵来衡量两个随机分布的差距，当两个随机分布相同时，其相对熵为0.当两个随机分布的差别增加时，器相对熵也增加。我们下面的实验是为了横量概率分布的差异。

试验方法、要求和材料

要求：

    1.任意摘录一段文字，统计这段文字中所有字符的相对频率。假设这些相对频率就是这些字符的概率（即用相对频率代替概率）；

    2.另取一段文字，按同样方法计算字符分布概率；

    3.计算两段文字中字符分布的KL距离；

    4.举例说明（任意找两个分布p和q）,KL距离是不对称的，即D(p//q)!=D(q//p);

方法：

D（p//q）=sum(p(x)*log(p(x)/q(x)))。其中p(x)和q(x)为两个概率分布

约定 0*log(0/q(x))=0;p(x)*log(p(x)/0)=infinity;

具体实验可参考：http://www.cnblogs.com/finallyliuyu/archive/2010/03/12/1684015.html