MIT 18.06 linear algebra lecture 1 方程组的几何解释 笔记
线性代数的基本问题是解方程组:
\[\begin{aligned}
2x-y &= 0 \\
-x+2y &= 3
\end{aligned}
\]
从几何的角度,可以从行图像、列图像两个角度解决方程组
row picture
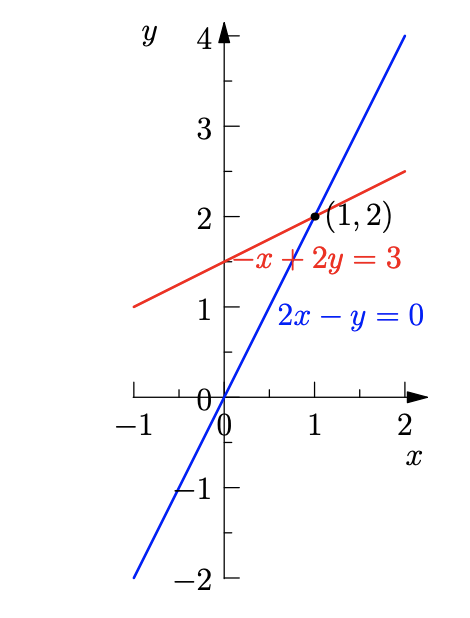
在例子中方程组的每个等式,是二维空间内的一条直线,显然两个等式所代表直线的交点,便是该方程组的解。
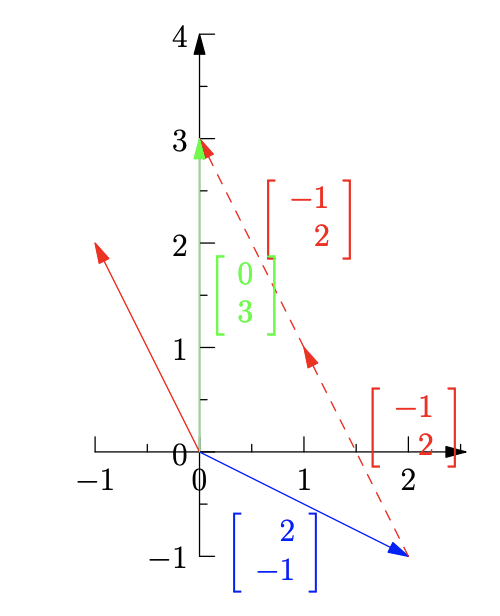
column picture
从列图像的角度,用向量的乘法和加法将方程组写为一个等式
\[x
\begin{bmatrix}
2\\
-1
\end{bmatrix}
+y
\begin{bmatrix}
-1\\
2
\end{bmatrix}=
\begin{bmatrix}
0\\
3
\end{bmatrix}
\]
问题就转变为寻找标量\(x\)和\(y\)。
matrix multiplication
将上面的方程组写为矩阵和向量相乘的形式
\[\begin{bmatrix}
2 & -1\\
-1 & 2
\end{bmatrix}
\begin{bmatrix}
x\\
y
\end{bmatrix}=
\begin{bmatrix}
0\\
3
\end{bmatrix}
\]
矩阵\(A=\begin{bmatrix} 2 & -1\\ -1 & 2 \end{bmatrix}\)称为系数矩阵,向量\(\boldsymbol{x}=\begin{bmatrix} x\\ y \end{bmatrix}\)是未知数向量。等式右边的部分组成向量\(\boldsymbol{b}\)。则
\[A\boldsymbol{x}=\boldsymbol{b}
\]
将矩阵\(A\)和向量\(\boldsymbol{x}\)相乘,即矩阵的列向量的线性组合。
\[\begin{bmatrix}
2 & 5\\
1 & 3
\end{bmatrix}
\begin{bmatrix}
1\\
2
\end{bmatrix}=1
\begin{bmatrix}
2\\
1
\end{bmatrix}+2
\begin{bmatrix}
5\\
3
\end{bmatrix}=
\begin{bmatrix}
12\\
7
\end{bmatrix}
\]
另外也可以按国内大学教科书所教授的行列相乘,逐一计算(不推荐)。
Linear Independence
对于下面的式子,是否每个\(\boldsymbol{b}\)都存在对应的解\(\boldsymbol{x}\)?也可以换种说法:矩阵\(A\)的列向量的线性组合是否能够覆满\(xy\)平面。
\[A\boldsymbol{x}=\boldsymbol{b}
\]
如果不行的话,称\(A\)是奇异矩阵(singular matrix),矩阵中的列向量是线性相关(linearly dependent)的,在二维空间内,列向量的线性组合为一个点或者一条线,在三维空间内为一个点、一条线或者一个平面。



