图

1.学习总结

1.1图的思维导图

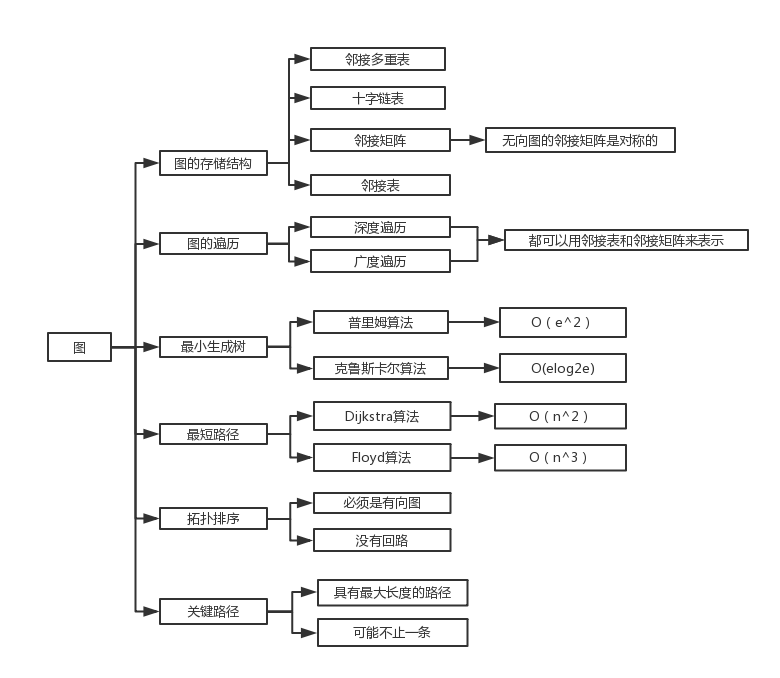
1.2 图结构学习体会

  • 深度遍历算法和广度遍历算法：这两种遍历都可以遍历出整个图，但是深度遍历对于新手来说还是有一点点小难度，但是熟悉了之后发现也就那样，对吧。但是还是需要去认真去理解。
  • Prim和Kruscal算法：这两种算法都是算最小生成树的，Krusca是直接从最小权重连接，而Prim是直接连接的。
  • Dijkstra算法和Foled算法：Foled算法到后面可以更改相对应的最小路径而Dijkstra算法一旦确定就无法更改。
  • 拓扑排序算法：这个拓扑排序不允许有回路，而且只能在有向图里。

2.PTA实验作业

7-1 图着色问题

2.2 设计思路

2.3 代码截图

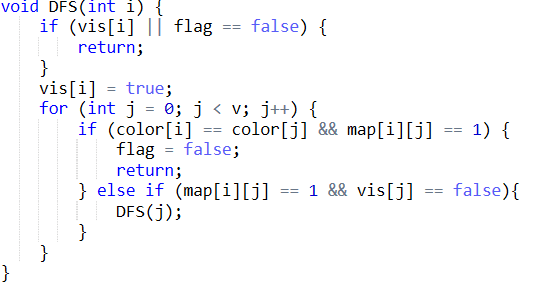
2.4 PTA提交列表说明

2.1 题目2  

7-5 畅通工程之最低成本建设问题

2.2 设计思路

这题就是你先把这个道路的邻接矩阵建立起来，然后用Prim算法算出他们最小权重的和，如果可以遍历到所有的城镇则输出需要的钱，如果没有则输出Impossible。这题的思路和7-4的一毛一样。

2.3 代码截图

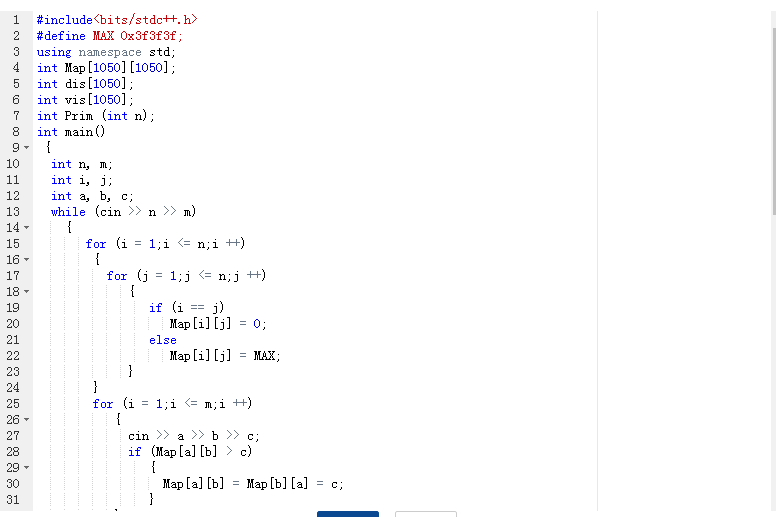
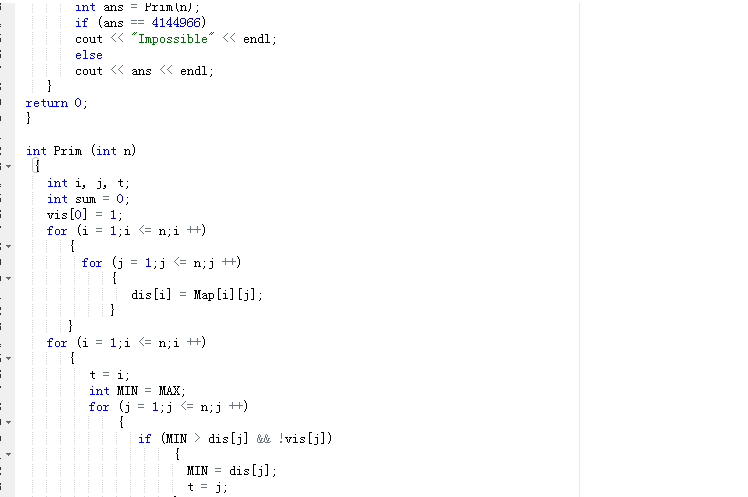
2.4 PTA提交列表说明

2.1 题目1：题目名称

7-2 排座位

2.2 设计思路

先创建find函数来寻找一个点的最后一个节点，如果没到最后一个，就往下一个寻找；

创建add合并函数，用来对自己的下一个点赋值；

最后使用main函数进行判断和输出。

2.3 代码截图

3.截图本周题目集的PTA最后排名

3.1 PTA排名

3.2 我的总分：217

4. 阅读代码

7-9 天梯地图

  1. #include <cstdio>  
  2. #include <algorithm>  
  3. #include <vector>  
  4. using namespace std;  
  5. const int inf = 999999999;  
  6. int dis[510], Time[510], e[510][510], w[510][510], Timepre[510], weight[510];  
  7. bool visit[510];  
  8. vector<int> Timepath, dispath, temppath, dispre[510];  
  9. int st, fin, minnode = inf;  
  10. void dfsTimepath(int v) {  
  11.     Timepath.push_back(v);  
  12.     if(v == st) {  
  13.         return ;  
  14.     }  
  15.     dfsTimepath(Timepre[v]);  
  16. }  
  17.   
  18. void dfsdispath(int v) {  
  19.     temppath.push_back(v);  
  20.     if(v == st) {  
  21.         if(temppath.size() < minnode) {  
  22.             minnode = temppath.size();  
  23.             dispath = temppath;  
  24.         }  
  25.         temppath.pop_back();  
  26.         return ;  
  27.     }  
  28.     for(int i = 0; i < dispre[v].size(); i++) {  
  29.         dfsdispath(dispre[v][i]);  
  30.     }  
  31.     temppath.pop_back();  
  32. }  
  33. int main() {  
  34.     fill(dis, dis + 510, inf);  
  35.     fill(Time, Time + 510, inf);  
  36.     fill(weight, weight + 510, inf);  
  37.     fill(e[0], e[0] + 510 * 510, inf);  
  38.     fill(w[0], w[0] + 510 * 510, inf);  
  39.     int n, m;  
  40.     scanf("%d %d", &n, &m);  
  41.     int a, b, flag, len, t;  
  42.     for(int i = 0; i < m; i++) {  
  43.         scanf("%d %d %d %d %d", &a, &b, &flag, &len, &t);  
  44.         e[a][b] = len;  
  45.         w[a][b] = t;  
  46.         if(flag != 1) {  
  47.             e[b][a] = len;  
  48.             w[b][a] = t;  
  49.         }  
  50.     }  
  51.     scanf("%d %d", &st, &fin);  
  52.   
  53.     Time[st] = 0;  
  54.     for(int i = 0; i < n; i++) {  
  55.         Timepre[i] = i;  
  56.     }  
  57.     for(int i = 0; i < n; i++) {  
  58.         int u = -1, minn = inf;  
  59.         for(int j = 0; j < n; j++) {  
  60.             if(visit[j] == false && Time[j] < minn) {  
  61.                 u = j;  
  62.                 minn = Time[j];  
  63.             }  
  64.         }  
  65.         if(u == -1) break;  
  66.         visit[u] = true;  
  67.         for(int v = 0; v < n; v++) {  
  68.             if(visit[v] == false && w[u][v] != inf) {  
  69.                 if(w[u][v] + Time[u] < Time[v]) {  
  70.                     Time[v] = w[u][v] + Time[u];  
  71.                     Timepre[v] = u;  
  72.                     weight[v] = weight[u] + e[u][v];  
  73.                 } else if(w[u][v] + Time[u] == Time[v] && weight[v] > weight[u] + e[u][v]) {  
  74.                     weight[v] = weight[u] + e[u][v];  
  75.                     Timepre[v] = u;  
  76.                 }  
  77.             }  
  78.         }  
  79.     }  
  80.     dfsTimepath(fin);  
  81.   
  82.     fill(visit, visit + 510, false);  
  83.     dis[st] = 0;  
  84.     for(int i = 0; i < n; i++) {  
  85.         int u = -1, minn = inf;  
  86.         for(int j = 0; j < n; j++) {  
  87.             if(visit[j] == false && minn > dis[j]) {  
  88.                 u = j;  
  89.                 minn = dis[j];  
  90.             }  
  91.         }  
  92.         if(u == -1) break;  
  93.         visit[u] = true;  
  94.         for(int v = 0; v < n; v++) {  
  95.             if(visit[v] == false && e[u][v] != inf) {  
  96.                 if(e[u][v] + dis[u] < dis[v]) {  
  97.                     dis[v] = e[u][v] + dis[u];  
  98.                     dispre[v].clear();  
  99.                     dispre[v].push_back(u);  
  100.                 } else if(e[u][v] + dis[u] == dis[v]) {  
  101.                     dispre[v].push_back(u);  
  102.                 }  
  103.             }  
  104.         }  
  105.     }  
  106.     dfsdispath(fin);  
  107.     printf("Time = %d", Time[fin]);  
  108.     if(dispath == Timepath) {  
  109.         printf("; Distance = %d: ", dis[fin]);  
  110.     } else {  
  111.         printf(": ");  
  112.         for(int i = Timepath.size() - 1; i >= 0; i--) {  
  113.             printf("%d", Timepath[i]);  
  114.             if(i != 0) printf(" => ");  
  115.         }  
  116.         printf("\n");  
  117.         printf("Distance = %d: ", dis[fin]);  
  118.     }  
  119.     for(int i = dispath.size() - 1; i >= 0; i--) {  
  120.         printf("%d", dispath[i]);  
  121.         if(i != 0) printf(" => ");  
  122.     }  
  123.     return 0;  
  124. }  

　　用两个Dijkstra + DFS。一个求最快路径（如果相同求路径的那条），一个求最短路径（如果相同求结点数最小的那条）。求最快路径可以直接在Dijkstra里面求前驱结点Timepre数组。求最短路径因为要求结点数最小的那条，所以要用dispre的二维数组存储所有结点的最短路径，然后用DFS求出满足条件的结点数最小的那条。

posted @ 2018-06-18 17:46  曾_钰尧  阅读(152)  评论(0)  编辑  收藏  举报