CF467C George and Job (DP)
Codeforces Round #267 (Div. 2)
|
C. George and Job
time limit per test
1 secondmemory limit per test
256 megabytesinput
standard inputoutput
standard outputThe new ITone 6 has been released recently and George got really keen to buy it. Unfortunately, he didn't have enough money, so George was going to work as a programmer. Now he faced the following problem at the work. Given a sequence of n integers p1, p2, ..., pn. You are to choose k pairs of integers:
in such a way that the value of sum Input
The first line contains three integers n, m and k (1 ≤ (m × k) ≤ n ≤ 5000). The second line contains n integers p1, p2, ..., pn (0 ≤ pi ≤ 109). Output
Print an integer in a single line — the maximum possible value of sum. Sample test(s)
Input
5 2 1 Output
9 Input
7 1 3 Output
61 |
题意:
给出n,m,k,给出由n个数组成的序列,在其中选出k组不重叠的连续m个数,使选择的数的和最大。
题解:
DP。
f[i][j],表示在[1,i]中选了j个区间得到的最大的和。
由于要经常求某连续m个数的和,可以先预处理出所有连续m个数的和,sum[i]表示以i为结尾的连续m个数的和。
最后结果为f[n][k]。
状态转移:
1 mf1(f);///全部置为-1 2 FOR(i,0,n) f[i][0]=0; 3 FOR(i,1,n){ 4 FOR(j,1,k){ 5 f[i][j]=f[i-1][j]; 6 if(i-m>=0 && f[i-m][j-1] != -1) f[i][j]=max(f[i][j],f[i-m][j-1]+sum[i]); 7 } 8 }
全代码:

1 //#pragma comment(linker, "/STACK:102400000,102400000") 2 #include<cstdio> 3 #include<cmath> 4 #include<iostream> 5 #include<cstring> 6 #include<algorithm> 7 #include<cmath> 8 #include<map> 9 #include<set> 10 #include<stack> 11 #include<queue> 12 using namespace std; 13 #define ll long long 14 #define usll unsigned ll 15 #define mz(array) memset(array, 0, sizeof(array)) 16 #define mf1(array) memset(array, -1, sizeof(array)) 17 #define minf(array) memset(array, 0x3f, sizeof(array)) 18 #define REP(i,n) for(i=0;i<(n);i++) 19 #define FOR(i,x,n) for(i=(x);i<=(n);i++) 20 #define RD(x) scanf("%d",&x) 21 #define RD2(x,y) scanf("%d%d",&x,&y) 22 #define RD3(x,y,z) scanf("%d%d%d",&x,&y,&z) 23 #define WN(x) printf("%d\n",x); 24 #define RE freopen("D.in","r",stdin) 25 #define WE freopen("1biao.out","w",stdout) 26 #define mp make_pair 27 #define pb push_back 28 const double eps=1e-10; 29 const double pi=acos(-1.0); 30 int a[5111]; 31 ll sum[5111]; 32 ll f[5111][5111];///f[i][j],到i时选了j个区间 33 int n,m,k; 34 int main(){ 35 int i,j; 36 RD3(n,m,k); 37 FOR(i,1,n){ 38 RD(a[i]); 39 } 40 ll sm=0; 41 FOR(i,1,n){ 42 sm+=a[i]; 43 if(i>=m){ 44 sum[i]=sm; 45 sm-=a[i-m+1]; 46 } 47 } 48 mf1(f);///全部置为-1 49 FOR(i,0,n) f[i][0]=0; 50 FOR(i,1,n){ 51 FOR(j,1,k){ 52 f[i][j]=f[i-1][j]; 53 if(i-m>=0 && f[i-m][j-1] != -1) f[i][j]=max(f[i][j],f[i-m][j-1]+sum[i]); 54 } 55 } 56 printf("%I64d\n",f[n][k]); 57 return 0; 58 }


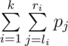 is maximal possible. Help George to cope with the task.
is maximal possible. Help George to cope with the task.

