A Class of Blind Source Extraction Method Using Second-Order Statistics

基于二阶统计量的盲源提取方法[1]。

文中提出了一系列基于二阶统计量的算法，包括离线BSE和在线BSE算法，可以提取平稳信号和非平稳信号。这些算法中，通过挖掘信号特征，提出了新的打分函数，以及一个无参数的自适应步长最速下降法用来得到最优提取权重向量。仿真实验证明提出的算法可以逐个重建源信号，并且性能优于基于高阶统计量的BSE方法。

此外，无参数自适应步长最速下降法具有若干优点：不需要调节参数，低运算量，不需要多余预处理步骤。

引言及建模

 相比于BSS同时恢复所有源信号，BSE是每次恢复一个源信号，因此其运算量更低，算法更灵活。通常采用高阶统计量HOS来解决BSE问题。此外，可以采用源信号的二阶统计量特性，其可以潜在地解决HOS要求的非高斯性假设。

经典的二阶统计量通常由以下两步组成：1）观测信号的预白化，将其降维为正交矩阵；2）将上述正交矩阵对角化为一个合适的协方差矩阵，得到其逆矩阵。

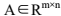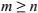假设n个unobservable的分量s(t) 是零均值并且互相统计独立。得到m个观测信号x(t)=As(t) 。其中是非奇异矩阵并且满秩。t=0,1,...,N-1为采样持续时间。BSE的目标就是从观测信号中逐个恢复源信号，提取信号可以表示为：。当时，提取权重向量w时一个m列向量，使得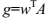。如果只有g的一个非零元素，则y(t)是恢复源信号或者s(t)的估计，并和g有同样的非零点。

基于二阶统计量的BSE算法

代价函数

使得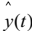为y(t)的线性预测信号，则

其中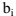是长度为P的线性预测器的系数。对于平稳源信号，y(t)及其最优估计的关系可以表述为下式，其中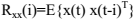

    或者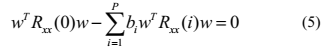

本文用公式(5)等式左边来估计提取向量w。下文中，i,P将被代替。为了减小运算量，我们假设线性预测器的系数均为1/。得到归一化代价函数为：

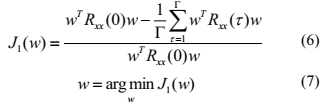
从公式(7)中，最优w可以从最小化代价函数(6)估计得到。

代价函数的可行性分析

下面我们来分析代价函数的可行性。为了简化分析，我们将公式(6)简化为下式：

通过解决下述广义特征值问题可以得到向量w：

其中和w分别是等式左边的特征值和特征向量。如果，则有：

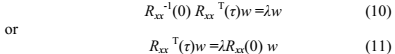
上述表明w也是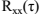和的特征向量。

不失广泛性，文中假设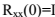，重写(11)得到

                             

 优化问题可以表述为:

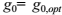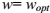上述问题的解是一个只有一个非零向量的。当时可能得到(13)中的最小值。从g的定义可知，可能只有时才会得到。

自相关估计

 上一小节的分析和结论可扩展至，只适合平稳情况下。此处分析的是提取非平稳源信号的代价函数：

其中是第k块的观测信号，并有：

代价函数的在线版本可以表述为：

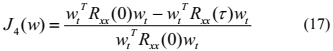
则观测信号的自相关可以由下式估计得到：

 

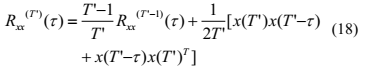
deflation处理

一个源信号被提取出来后，可以将其从观测信号中移除。可以通过一个deflation步骤实现。

          

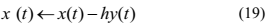
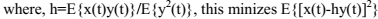
当提取出一个源信号后，则N个混合信号对应N-1个源信号，此时可以通过PCA降维至N-1维。

无参数自适应步长的最速下降法

为了得到(6),(14)和(17)中的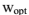，采用最速下降法更新w来最小化代价函数：

 

 提出的新方法为：

 

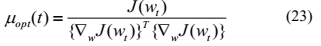
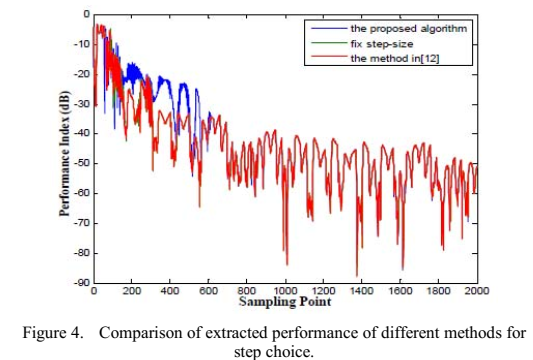
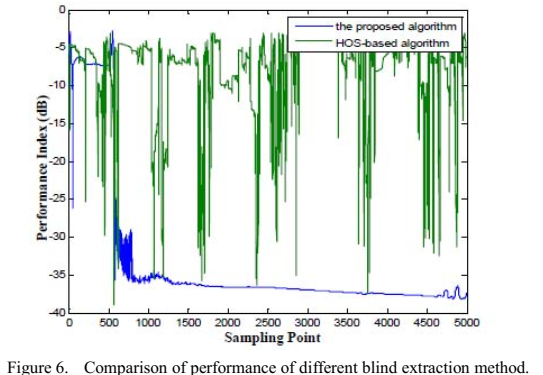
仿真实验

在matlab2010b上验证，3个平稳源信号，三个非平稳源信号（语音信号）。【文中涉及的是线性瞬时混合】

    

参考文献

[1] A Class of Blind Source Extraction Method Using Second-Order Statistics. 2017 INTERNATIONAL CONFERENCE ON ROBOTICS AND AUTOMATION SCIENCES (ICRAS).