Python线性回归算法【解析解，sklearn机器学习库】

一.概述

　　参考博客：https://www.cnblogs.com/yszd/p/8529704.html

二.代码实现【解析解】

import numpy as np
import matplotlib.pyplot as plt

__author__ = 'zhen'

# 这里相当于是随机X维度X1，rand是随机均匀分布
X = 2 * np.random.rand(100, 1)
# 人为的设置真实的Y一列，np.random.randn(100, 1)是设置error，randn是标准正太分布
y = 3 + 6 * X + np.random.randn(100, 1)
# 整合X0和X1
X_b = np.c_[np.ones((100, 1)), X] #combine聚合两数据集
# print(X_b)

# 常规等式求解theta
# invert
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
print(theta_best)

# 创建测试集里面的X1
X_new = np.array([[0], [2]]) 
X_new_b = np.c_[(np.ones((2, 1))), X_new]
print(X_new_b)
y_predict = X_new_b.dot(theta_best)
print(y_predict)

plt.plot(X_new, y_predict, 'r-')
plt.plot(X, y, 'b.')
plt.axis([0, 2, 0, 15])
plt.show()

三.结果【解析解】

 　　

　　可视化：

　　

 

 四.代码实现【sklearn机器学习库】

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

__author__ = 'zhen'

X = 2 * np.random.rand(100, 1)
y = 3 + 6 * X + np.random.randn(100, 1)

lin_reg = LinearRegression()
lin_reg.fit(X, y)
print(lin_reg.intercept_, lin_reg.coef_)

X_new = np.array([[0], [2]])
y_predict = lin_reg.predict(X_new)
print(y_predict)

# 可视化
plt.plot(X_new, y_predict, 'r-')
plt.plot(X, y, 'b.')
plt.axis([0, 2, 0, 15])
plt.show()

五.结果【sklearn机器学习库】

 　　

 

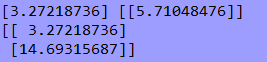
 　　可视化：

　　

 

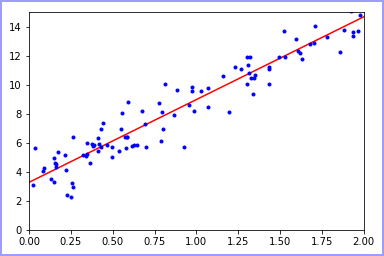
 六.总结

　　根据图示可以得出结论，使用解析解或者是sklearn机器学习库都可以得到大致的结论，所花费时间和达到的效率都比较类似。但这仅限于一元线性回归，当参数类别增加时，使用解析解会大大增加程序复杂程度和计算耗能，因此建议多使用sklearn库，并根据情况进行参数配置和优化。