排序之堆排序
前言
本篇博客是在伍迷兄的博客基础上进行的，其博客地址点击就可以进去，里面好博客很多，我的排序算法都来自于此；一些数据结构方面的概念我就不多阐述了，伍迷兄的博客中都有详细讲解，而我写这些博客只是记录自己学习过程，加入了一些自己的理解，同时也希望给别人提供帮助。
前提故事
今天，骚年找到博主，叹了一声：“唉”
博主道：“年纪轻轻的，唉什么？”
骚年说：“博主，我看了你的简单选择排序，自己也去实现了，发现确实好理解，但是，我却发现它做了好多多余的事，连鱼都不如”
博主顿时懵了，道:“连鱼都不如是什么意思？”
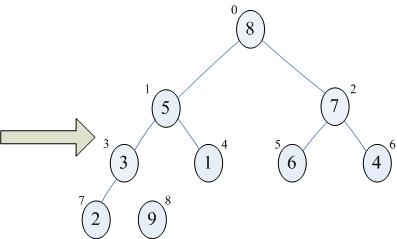
骚年到：“鱼都有7秒的记忆，简单选择排序却记忆都没有，比过之后还是不知道彼此之间的大小关系，下次还得重新比较，你看如下
当i=0
3和7有个比较过程，结尾当5和1交换之后
当i=1时，
3和7又有一个比较过程，那么之前的那次比较就根本没有记录下来，如果记录下来了，那么这次就不用比较了”。
博主：“恩，你说的有道理，那你有什么办法让他有记忆吗？”。
骚年：“有的话就不会叹气了，唉！”。
博主：“别叹气，应该有这方面的解决办法的，我们查查资料”。
两位就开始了苦逼的查询之旅，最终找到了堆排序！
基本思想
什么是堆？堆是具有下列性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图
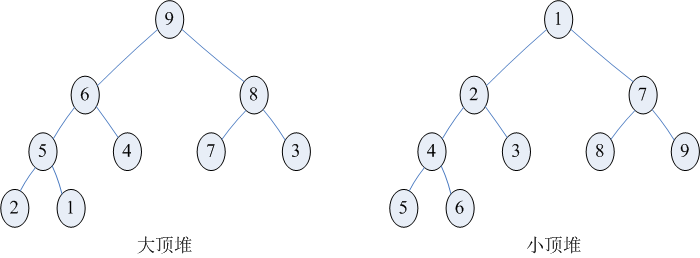
从完全二叉树的性质可知（不懂的可以去查看下数据结构，伍迷兄的博客上就有介绍，博客地址），下标为i的节点的左右孩子分别是i*2+1和i*2+2
堆排序（Heap Sort）就是利用堆（假设利用大顶堆）进行排序的方法。它的基本思想是，将待排序的序列构造成一个大顶堆。此时，整个序列的最大值就是堆顶的根结点。将它移走（其实就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值），然后将剩余的n-1个(0...n-1)序列重新构造成一个堆，这样就会得到n个元素中的次小值。 如此反复执行，便能得到一个有序序列了。
这时候有人就问了：“之前说简单选择排序没有记忆功能，难道这堆就有？ 我也没看出来呀！”
其实堆是有记忆功能的，就是因为他自身的结构，每个结点的值都大于或等于其左右孩子结点的值（这是大顶堆，小顶堆则是每个结点的值都小于或等于其左右孩子结点的值），这就是记忆！当你将整个序列构建成一个堆之后，那么结点元素是比左右孩子大或者小的，这就是记忆！，还有点迷糊的小伙伴，可以先放一放这个问题，到时候回过头来就明白了。
代码实现
1 /** 2 * 堆排序 3 * @param arr 4 */ 5 public void heapSort(int[] arr){ 6 int len = arr.length; 7 //构建初始大顶堆 8 for(int i=len/2-1; i>=0; i--){ 9 heapAdjust(arr,i,len-1); 10 } 11 12 //交换堆顶元素和未排序序列的最后一个元素,并重新构建大顶堆 13 for(int i=len-1; i>0; i--){ 14 swap(arr,0,i); // 元素交换 15 heapAdjust(arr,0,i-1); 16 } 17 } 18 19 /** 20 * 将arr[pos...off]构建成大顶堆 21 * @param arr 22 * @param pos 23 * @param off 24 */ 25 public void heapAdjust(int[] arr, int pos, int off){ 26 int j,temp=arr[pos]; 27 for(j=pos*2+1; j<=off; j=j*2+1){ 28 if(j<off && arr[j]<arr[j+1]){ 29 ++j; 30 } 31 // 节点不小于左右孩子节点 32 if(temp >= arr[j]){ 33 break; 34 } 35 arr[pos] = arr[j]; 36 pos = j; 37 } 38 arr[pos] = temp; 39 }
关键点：（1）如何由一个无序序列构建成一个堆
（2）如果在输出堆顶元素后，调整剩余元素成为一个新的堆
执行过程模拟
从代码中也可以看出，整个排序过程分为两个for循环。第一个循环要完成的就是将现在的待排序序列构建成一个大顶堆。第二个循环要完成的就是逐步将每个最大值的根结点与末尾元素交换，并且再调整其成为大顶堆。
假设我们要排序的序列是{5,3,7,9,1,6,4,8,2}，那么len=arr.length=9，第一个for循环，代码第4行，i是从len/2-1=3开始，3→2→1→0的变量变化。为什么不是从0到8，或者从8到0，
而是从3到0呢？其实我们看了下图就明白了，它们都有什么规律？它们都是有孩子的结点。注意灰色结点的下标编号就是0、1、2、3。
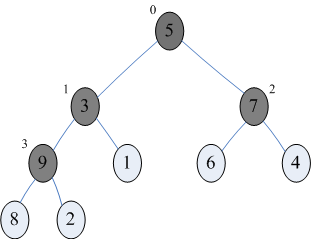我们所谓的将待排序的序列构建成为一个大顶堆，其实就是从下往上，从右到左，将每个非终端结点（非叶结点）当作根结点，将其和其子树调整成大顶堆。i的3→2→1→0的变量变化，其实也就是9，7，3，5的结点调整过程。
既然已经弄清楚i的变化是在调整哪些元素了，现在我们来看关键的heapAdjust（堆调整）函数是如何执行的。
1）heapAdjust第一次被调用时，pos=3，off=8，arr={5,3,7,9,1,6,4,8,2}
2）第26行，temp=arr[3]=9,如下图：
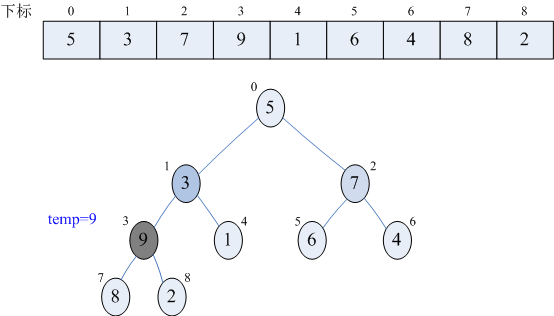
3）第27～37行，循环遍历其结点的孩子。这里j变量为什么是从2*pos+1开始呢？又为什么是j=j×2+1递增呢？原因还是二叉树的性质，因为我们这棵是完全二叉树，当前结点序号是pos，其左孩子的序号一定是2s+1，右孩子的序号一定是(2s+1)+1，它们的孩子当然也是以2的位数序号增加，因此j变量才是这样循环 (+1是因为数组下标是从0开始的，这里需要注意)。
4）第28～30行，此时j=2×pos+1=7 < off说明不是最后一个结点，如果arrr[j]<arr[j+1]，则说明左孩子小于右孩子，我们的目的是要找到较大值，当然需要让j+1以便变成指向右孩子的下标。当前9的左右孩子分别是8和2，并不满足条件，所以j还是等于7。
5）第32～34行，temp=9 >= arr[j]=8,条件满足，break，跳出循环。
6）第38行，执行arr[pos]即arr[3]=temp=9。本次函数调用完成，没有元素进行交换，整个序列没有变化。
7）再次调用heapAdjust，此时pos=2，off=8，temp=arr[2]=7,第28～30行，6>4,j不变，j=5，temp=7 > arr[j]=6,跳出循环，arr[pos]=temp=7,整个序列没有变化。
8）再次调用heapAdjust，此时pos=1，off=8，temp=arr[1]=3,第28～30行，9>1,j不变，j=3，temp=3 < arr[j]=9,第35～36行，arr[1]被赋值了9,pos=3,继续执行循环，j=j×2+1=7 < off,执行循环体，使得arr[3]被赋值了8，循环执行完后，arr[7]被赋值了3，函数调用结束。本次调用使得3，9，8进行了轮换。
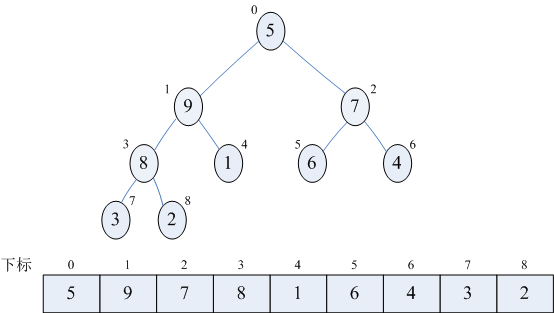
9）再次调用heapAdjust，此时pos=0，off=8，temp=5，第28～30，9>7,j不变，j=1，第35～36行，arr[0]被赋值了9，并且pos=1，继续执行循环，j=3 < off,执行循环体，使得arr[1]被赋值了8，并且pos=3，继续执行循环，j=7 < off,执行循环体，第28～30行，3>2,j不变，第32行，temp>arr[j],跳出循环，最arr[3]被赋值了5，函数调用结束。本次调用使得5，9，8进行了轮换。
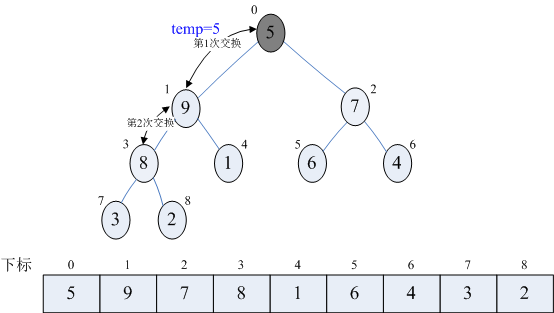
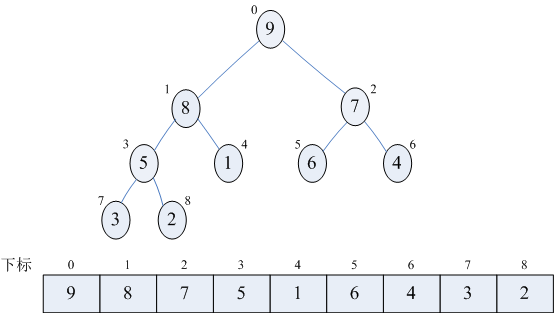
到此为止，我们构建大顶堆的过程算是完成了，也就是第8～10行循环执行完毕。或许是有点复杂，如果不明白，多试着模拟计算机执行的方式走几遍，应该就可以理解其原理。
接下来的第13～16行就是正式的排序过程，由于有了前面的充分准备，其实这个排序就比较轻松了。
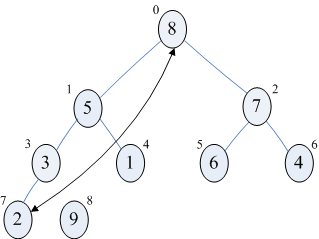
a）当i=len-1=8时，交换9和2，然后调整arr[0...7],使之成为一个大顶堆，调整过程和刚才一样，此时序列为{8,5,7,3,1,6,4,2,9}，如下图
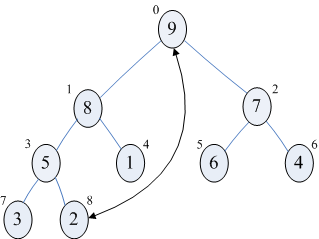
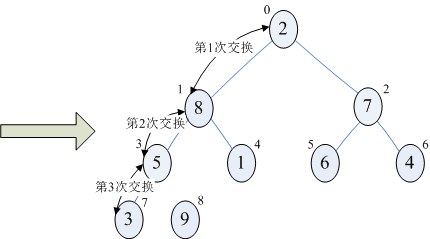
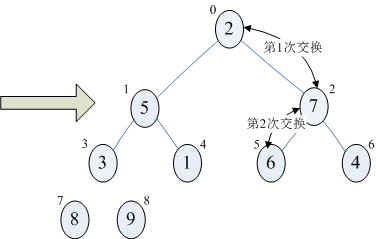
b）当i=7时，交换8和2，然后调整arr[0...6],使之成为一个大顶堆，此时序列为{7,5,6,3,1,2,4,8,9},如下图
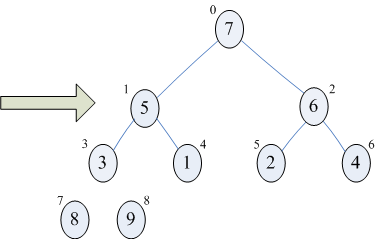
c）后面的变化完全类似，这里就不演示了，就当留给大家练手的东西，一定要亲手去模拟哦！
至此，序列就有序了，为{1,2,3,4,5,6,7,8,9}。
总结
此算法不好想到，一般人根本就想不到，只能由衷的佩服这个算法的提出者，太厉害了；首先由普通的数列联想到完全二叉树，然后利用完全二叉树的特性来实现记忆的功能，从而提高运行效率，厉害，厉害！
一定要注意大顶堆的特点，有些人不理解，heapAdjust函数已经是构建大顶堆了，为什么构建初始大顶堆的时候需要一个for循环来实现？另外，之后的大顶堆构建为什么只用调用一次heapAdjust就可以了？ 其实后面的果是前面种下的因得来的，你可以试着去掉构建初始大顶堆的for循环，你会发现，初始大顶堆都构建不出来（不排序特殊情况），有疑问的可以自己去试试！
实践是检验真理的唯一标准！一定要动手去实践！
