排序系列算法——归并排序

      归并排序是采用分治策略进行排序的一种算法，其基本原理是将未排序的数组划分为两个子数组，分别对两个子数组尽心排序，然后将有序的子数组合并。归并排序分为两个过程：一是数组划分为两个子数组并分别进行排序，二是将两个已排序的子数组进行合并。

 

将数组划分为两个子数组并进行排序

      将数组一分为二很简单，关键是划分之后如何排序的问题。归并排序的做法是对数组不断进行划分，直到不能划分为止或者说不需要划分为止，怎样才算不需要再划分呢？当子数组只剩下一个或者两个的时候就不用继续划分了，一个元素本来就是有序的，两个元素只要对比一下双方的大小就可以轻而易举的完成排序的工作。当两个子数组都是有序时，将两个字数组合并成为一个有序的数组，然后不断重复字数组合并的工作就可以完成原始数组的排序。

以一个实例说明：对数组{13,8,15,9,5,12,11}按从小到大进行排序。

 

                                                                                    图1 归并排序示意图

两个子数组进行合并

从上图可以看出，归并排序其中一个很重要的步骤是对已经排好序的子数组进行合并。以一个实例来说明合并的步骤：

 

 

 

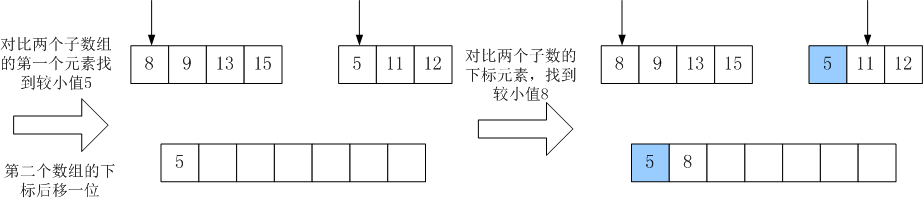
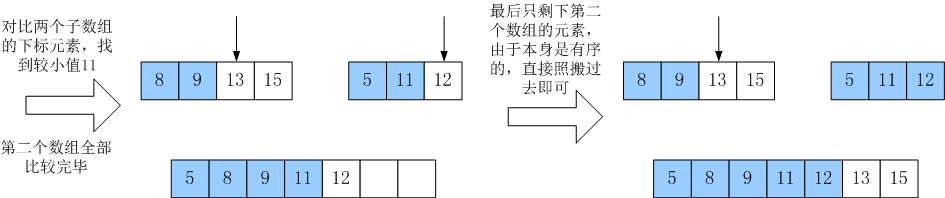
C++源码

先给出两个有序子数组合并的代码：

void Merge(int array[],int p,int q,int r){
    int *temp1 = new int[q-p+1];
    int *temp2 = new int[r-q];
    for(int i=p;i<=q;i++){
        temp1[i-p]=array[i];
    }
    for(int i=q+1;i<=r;i++){
        temp2[i-q-1]=array[i];
    }
    int k=0;
    int z=0;
    for(int i=p;i<=r;i++){
        if((temp1[k]<temp2[z]&&k<q-p+1)||z>=r-q){
            array[i]=temp1[k];
            k++;
        }
        else{
            array[i]=temp2[z];
            z++;
        }
    }
}

      归并排序划分合并其实是一个递归的过程，原始数组划分为两个子数组，两个子数组再细分成各自的子数组，直到子数组只剩下一个或者两个元素为止。最后将子数组逐步进行合并得出最后已排序的数组。

void MergeSort(int array[],int p,int q,int r){
    if(r-p==1){
        if(array[p]>array[r]){
            swap(array,p,r);
        }
        return;
    }
    if(r-p==0){
        return;
    }
    int t=floor((p+q)/2);
    int t1 =floor((q+1+r)/2);
    MergeSort(array,p,floor((p+q)/2),q);
    MergeSort(array,q+1,floor((q+1+r)/2),r);
    Merge(array,p,q,r);
}

所有源代码：

#include "stdafx.h"
#include <iostream>
using namespace std;

//两个位置的数据互换
void swap(int array[],int num1,int num2){
    int temp = array[num1];
    array[num1]=array[num2];
    array[num2]=temp;
}

//合并有序的两个序列
void Merge(int array[],int p,int q,int r){
    int *temp1 = new int[q-p+1];
    int *temp2 = new int[r-q];
    for(int i=p;i<=q;i++){
        temp1[i-p]=array[i];
    }
    for(int i=q+1;i<=r;i++){
        temp2[i-q-1]=array[i];
    }
    int k=0;
    int z=0;
    for(int i=p;i<=r;i++){
        if((temp1[k]<temp2[z]&&k<q-p+1)||z>=r-q){
            array[i]=temp1[k];
            k++;
        }
        else{
            array[i]=temp2[z];
            z++;
        }
    }
}

//归并排序
void MergeSort(int array[],int p,int q,int r){
    if(r-p==1){
        if(array[p]>array[r]){
            swap(array,p,r);
        }
        return;
    }
    if(r-p==0){
        return;
    }
    int t=floor((p+q)/2);
    int t1 =floor((q+1+r)/2);
    MergeSort(array,p,floor((p+q)/2),q);
    MergeSort(array,q+1,floor((q+1+r)/2),r);
    Merge(array,p,q,r);
}

int main(int argc, _TCHAR* argv[])
{
    int temp[]={6,10,4,7,15,12,8,11,9,5};
    MergeSort(temp,0,4,9);
    return 0;
}