机器学习基石笔记14——机器可以怎样学得更好(2)
转载请注明出处:http://www.cnblogs.com/ymingjingr/p/4271742.html
目录
机器学习基石笔记1——在何时可以使用机器学习(1)
机器学习基石笔记2——在何时可以使用机器学习(2)
机器学习基石笔记3——在何时可以使用机器学习(3)(修改版)
机器学习基石笔记4——在何时可以使用机器学习(4)
机器学习基石笔记5——为什么机器可以学习(1)
机器学习基石笔记6——为什么机器可以学习(2)
机器学习基石笔记7——为什么机器可以学习(3)
机器学习基石笔记8——为什么机器可以学习(4)
机器学习基石笔记9——机器可以怎样学习(1)
机器学习基石笔记10——机器可以怎样学习(2)
机器学习基石笔记11——机器可以怎样学习(3)
机器学习基石笔记12——机器可以怎样学习(4)
机器学习基石笔记13——机器可以怎样学得更好(1)
机器学习基石笔记14——机器可以怎样学得更好(2)
机器学习基石笔记15——机器可以怎样学得更好(3)
机器学习基石笔记16——机器可以怎样学得更好(4)
十四、Regularization
正则化。
14.1 Regularized Hypothesis Set
正则化假设。
上一章中提到了防止过拟合的五种措施,本章将介绍其中一种措施,正则化(Regularization)。
正则化的主要思想:将假设函从高次多项式的数降至低次,如同开车时的踩刹车,将速度降低,效果图如图14-1所示,右图表示高次多项式函数,明显产生了过拟合现象,而左图的表示使用正则化后的低次函数。
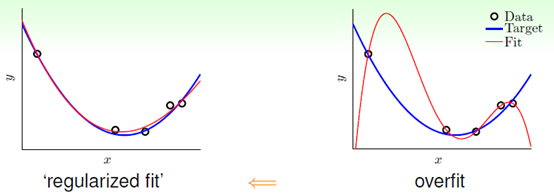
图14-1 正则化拟合与过拟合
已知高次多项式包含低次多项式,因此高次函数和低次函数的关系如图14-2所示,本章的内容是在使用高次函数过拟合时,如何将假设函数降低为低次,即如何从外围的大圈中回归到内部的小圈。
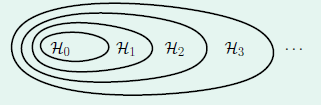
图14-2 高次函数与低次函数的关系图
"正则化"这个词来自于不适定问题(ill-posed problem)的函数逼近(function approximation),即在函数逼近中出现多个解,如何选择解的问题。
如何降次?该问题使用到前几章中提到的多项式转换与线性回归的知识,把降次的问题转换成带有限制(constraint)条件的问题。以下以10次多项式与二次式为例了解正则化,假设w的表达式分别如公式14-1与公式14-2。
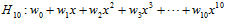 (公式14-1)
(公式14-1)
 (公式14-2)
(公式14-2)
公式14-2可以使用公式14-1加上如下限制条件表示,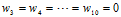 ,
,
因此10次多项式的假设空间与最小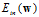 的表达式分别如公式14-3和公式14-4。
的表达式分别如公式14-3和公式14-4。
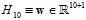 (公式14-3)
(公式14-3)
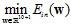 (公式14-4)
(公式14-4)
通过上述结论,2次式的假设空间与最小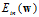 的表达式分别如公式14-5和公式14-6。
的表达式分别如公式14-5和公式14-6。
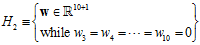 (公式14-5)
(公式14-5)
 (公式14-6)
(公式14-6)
如果将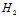 的条件设计的更宽松,表示成
的条件设计的更宽松,表示成 的形式,如公式14-7所示。
的形式,如公式14-7所示。
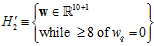 (公式14-7)
(公式14-7)
因此求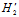 的最优化
的最优化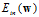 的问题如公式14-8所示。
的问题如公式14-8所示。
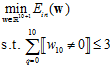 (公式14-8)
(公式14-8)
该假设空间与 、
、 的关系如公式14-9所示。
的关系如公式14-9所示。
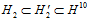 (公式14-9)
(公式14-9)
 假设空间又被称作稀疏(sparse)的假设空间,因为很多参数为0。注意公式14-8限制中的
假设空间又被称作稀疏(sparse)的假设空间,因为很多参数为0。注意公式14-8限制中的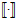 函数,表明该最优化问题为一个NP难问题。因此必须继续改进假设函数,产生假设空间
函数,表明该最优化问题为一个NP难问题。因此必须继续改进假设函数,产生假设空间 如公式14-10所示。
如公式14-10所示。
 (公式14-10)
(公式14-10)
假设空间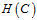 最优化
最优化 的问题如公式14-11所示。
的问题如公式14-11所示。
 (公式14-11)
(公式14-11)
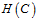 与
与 有重叠部分,但是并不完全一致。随着C的增大,
有重叠部分,但是并不完全一致。随着C的增大,  的假设空间也在增大,可以得到如公式14-12所示。
的假设空间也在增大,可以得到如公式14-12所示。
 (公式14-12)
(公式14-12)
称假设空间 为正则化假设空间,即假设限制条件的假设空间。正则化假设空间中最好的假设用符号
为正则化假设空间,即假设限制条件的假设空间。正则化假设空间中最好的假设用符号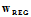 表示。
表示。
14.2 Weight Decay Regularization
权值衰减正则化。
为了表述的简便,将上一节的最优化公式14-11写成向量矩阵的形式,如公式14-13所示。
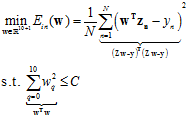 (公式14-13)
(公式14-13)
插一句,通常解释带有限制条件的最优化问题都会引用拉格朗日函数,林老师更深入的解释了拉格朗日乘子背后的因素。
首先绘制有限制条件的最优化示意图,图中蓝色部分为 ,红色部分为限制条件
,红色部分为限制条件 ,从表达公式不难得出两者一个为椭圆,一个为圆形(在高维空间中式超球体)。
,从表达公式不难得出两者一个为椭圆,一个为圆形(在高维空间中式超球体)。
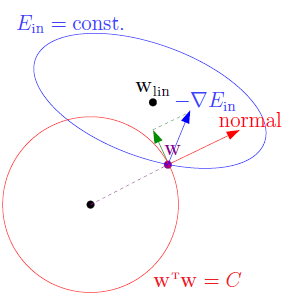
图14-4 有限制条件的最优化示意图
从前面的章节中了解在求解最小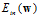 时,可用
时,可用 梯度的反方向,即
梯度的反方向,即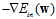 作为下降方向,但是与回归问题还有一些不同,此处多了限制条件
作为下降方向,但是与回归问题还有一些不同,此处多了限制条件 ,因此下降的方向不可以超出限制的范围,如图14-3中红色的向量为限制圆球切线的法向量,朝着该方向下降便超出了限制的范围,因此只可以沿着球切线的方向滚动,如图14-3中绿色的向量。何时降到最小?即实际滚动方向(图中蓝色的向量)不存在与球切线方向相同的分量,换句话说
,因此下降的方向不可以超出限制的范围,如图14-3中红色的向量为限制圆球切线的法向量,朝着该方向下降便超出了限制的范围,因此只可以沿着球切线的方向滚动,如图14-3中绿色的向量。何时降到最小?即实际滚动方向(图中蓝色的向量)不存在与球切线方向相同的分量,换句话说 与球切线的法向量w相平行,如公式14-14所示,其中
与球切线的法向量w相平行,如公式14-14所示,其中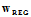 表示正则化最优解。
表示正则化最优解。
 (公式14-14)
(公式14-14)
加入拉格朗日乘子 ,可写成等式的形式,如公式14-15.
,可写成等式的形式,如公式14-15.
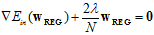 (公式14-15)
(公式14-15)
将线性回归中求得的 表达式(9.2节中求导过程)代入公式14-15,得公式14-16.
表达式(9.2节中求导过程)代入公式14-15,得公式14-16.
 (公式14-16)
(公式14-16)
求出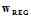 的表达式如公式14-17。
的表达式如公式14-17。
 (公式14-17)
(公式14-17)
其中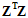 是半正定的,因此只要
是半正定的,因此只要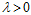 ,则保证
,则保证 为正定矩阵,必可逆。该回归形式被称为岭回归(ridge regression)。
为正定矩阵,必可逆。该回归形式被称为岭回归(ridge regression)。
是否还记得线性回归的直接形式,如公式14-18所示。
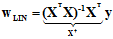 (公式14-18)
(公式14-18)
对公式14-15做成积分得公式14-19。
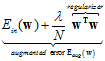 (公式14-19)
(公式14-19)
求公式14-19的最小解问题等价于公式14-19。其中该表达式称为增广错误(augmented error),用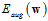 表示,其中
表示,其中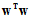 为正则化项(regularizer)。用无限制条件的
为正则化项(regularizer)。用无限制条件的 取代了上节中提到的有限制条件的
取代了上节中提到的有限制条件的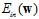 。实际上使用了拉格朗日函数,但林老师是反推过去,之所以叫做增广错误,是因为比传统的
。实际上使用了拉格朗日函数,但林老师是反推过去,之所以叫做增广错误,是因为比传统的 多了一正则化项。在
多了一正则化项。在 或
或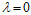 时(
时( 的情况是线性回归的求解),最小w的求解公式如公式14-20所示。
的情况是线性回归的求解),最小w的求解公式如公式14-20所示。
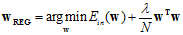 (公式14-20)
(公式14-20)
因此,不需要给出上一节中有条件的最小化问题中包含的参数C,而只需要给出增广错误中的参数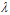 。
。
观察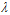 参数对最终求得的
参数对最终求得的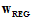 的影响,如图14-5。
的影响,如图14-5。

图14-5  参数对最终求得的
参数对最终求得的 的影响
的影响
在 时,过拟合,随着
时,过拟合,随着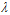 的不断增大变成了欠拟合状态。越大的
的不断增大变成了欠拟合状态。越大的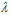 对应着越短的权值向量w,同时也对应着越小的约束半径C。(记得14.1节中如何处理欠拟合吗?将C尽量缩小,准确的说寻找小的权值向量w),因此这种将w变小的正则化,即加上
对应着越短的权值向量w,同时也对应着越小的约束半径C。(记得14.1节中如何处理欠拟合吗?将C尽量缩小,准确的说寻找小的权值向量w),因此这种将w变小的正则化,即加上 的正则化称为权重衰减(weight-decay)正则化。此种正则化,可以和任意的转换函数及任意的线性模型结合。
的正则化称为权重衰减(weight-decay)正则化。此种正则化,可以和任意的转换函数及任意的线性模型结合。
注意:在做多项式转换时,假设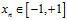 ,多项式转换函数为
,多项式转换函数为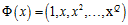 则在高次项
则在高次项 上时,数值非常小,为了和低次项对应的权值向量分量产生一致的影响力,则该项的权值
上时,数值非常小,为了和低次项对应的权值向量分量产生一致的影响力,则该项的权值 一定非常大,但是正则化求解需要特别小的权值向量w,因此需要转换后的多项式各项线性无关,即转换函数为
一定非常大,但是正则化求解需要特别小的权值向量w,因此需要转换后的多项式各项线性无关,即转换函数为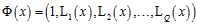 ,其各项为正交基函数(orthonormal basis functions),此多项式称为勒让德多项式(Legendre polynomials),多项式的前5项如图14-6所示。
,其各项为正交基函数(orthonormal basis functions),此多项式称为勒让德多项式(Legendre polynomials),多项式的前5项如图14-6所示。

图14-6 勒让德多项式的前5项表示
14.3 Regularization and VC Theory
正则化与VC理论。
本节介绍正则化与VC理论的关系。即从VC理论的角度说明为什么正则化的效果好(14.1节从过拟合的角度介绍正则化好的原因)。
最小化带限制条件的 与最小化
与最小化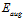 等价,因为参数C类似与参数
等价,因为参数C类似与参数 。通过7.4节的知识得知,
。通过7.4节的知识得知,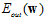 的上限可以表示为公式14-21的形式。
的上限可以表示为公式14-21的形式。
 (公式14-21)
(公式14-21)
因此,VC限制间接的保证了最小化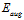 可以得到最小的
可以得到最小的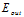 。
。
便于观察对比,将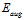 的表达式重复写一遍,如公式14-22。
的表达式重复写一遍,如公式14-22。
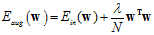 (公式14-22)
(公式14-22)
 上限更一般的形式可以写成公式14-23。
上限更一般的形式可以写成公式14-23。
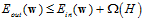 (14-23)
(14-23)
通过公式14-22与公式14-23的对比,更容易理解最小化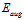 能获得比最小化
能获得比最小化 更好效果的原因。如公式14-22中正则化项
更好效果的原因。如公式14-22中正则化项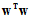 表示一个假设函数的复杂度;而公式14-23中的
表示一个假设函数的复杂度;而公式14-23中的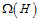 表示整个假设空间的复杂度,如果
表示整个假设空间的复杂度,如果 (
(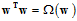 ,其中
,其中 表示该假设的复杂度)很好的代表
表示该假设的复杂度)很好的代表 ,则
,则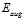 比
比 表现的更好。
表现的更好。
上述是通过VC限制通过一个启发式的方式说明正则化的优势,接下来通过VC维阐述正则化的好处。
将最小化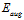 的形式写成公式14-24。
的形式写成公式14-24。
 (公式14-24)
(公式14-24)
按第七章的理论,VC维 , 在求解最小化时所有的假设函数
, 在求解最小化时所有的假设函数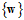 都将被考虑。但是因为参数C或者更直接的来说参数
都将被考虑。但是因为参数C或者更直接的来说参数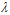 的限制,实际被考虑的只有
的限制,实际被考虑的只有 。因此有效的VC维
。因此有效的VC维 与两部分相关:假设空间H及算法A。实际的VC维很小意味着模型复杂度很低。
与两部分相关:假设空间H及算法A。实际的VC维很小意味着模型复杂度很低。
14.4 General Regularizers
一般化的正则化项。
本章的前几节介绍的正则化项是权值衰减的正则化项(weight-decay (L2) regularizer),或称为L2正则化项,标量形式为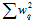 ,向量形式为
,向量形式为 。那么更一般的正则化项应该如何设计,或者一般化的正则化项的设计原则是什么?主要分为三点,如下:
。那么更一般的正则化项应该如何设计,或者一般化的正则化项的设计原则是什么?主要分为三点,如下:
依据目标函数(target-dependent),即根据目标函数的性质设计正则化项,如某目标函数是对称函数,因此权值向量的所有奇数分量应被抑制,可以设计成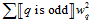 的形式,在奇数时增加;
的形式,在奇数时增加;
可以说得通(plausible):正则化项应尽可能地平滑(smooth)或简单(simpler),因为不论是随机性噪音还是确定性噪音都不是平滑的。平滑表示可微,如L2。简单表示容易求解,如L1正则化项或稀疏(sparsity)正则化项: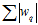 ,稍后介绍;
,稍后介绍;
友好:易于最优化的求解。如L2。
即使设计的正则化项不好也不用担心,因为还存在一个参数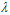 ,当其为0时,则正则化项不起作用。
,当其为0时,则正则化项不起作用。
回忆8.3节,错误衡量的设计原则,与此类似,依据用户(user-dependent),说得通,友好。
因此最终的增广错误由错误函数和正则化项两部分组成,如公式14-25所示。
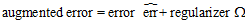 (公式14-25)
(公式14-25)
通过比较常用的两种正则化项(L2和L1)具体的解释上述设计原则。
L2的正则化示意图如图14-7所示,正则化项如公式14-26。
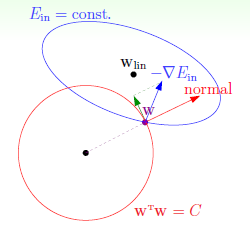
图14-7 L2正则化示意图
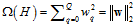 (公式14-26)
(公式14-26)
该正则化项在为凸函数,在每个位置都可以微分,因此比较容易计算。
再介绍一种新的正则化项L1,其示意图如图14-8所示正则化项如公式14-27。

图14-8 L1正则化项示意图
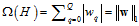 (公式14-27)
(公式14-27)
同样也是凸图形,但是并不是所有的位置都可微,如转角处。为何成为稀疏?假设菱形法相w全是不为零的分量,因此微分得的向量为分量全为1的向量。如果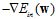 与该全为1的向量不平行,则向量一直会沿着菱形边界移动到顶点处,因此在顶点处产生最优解,最优解含有值为0的分量,因此为稀疏的解,计算速度快。
与该全为1的向量不平行,则向量一直会沿着菱形边界移动到顶点处,因此在顶点处产生最优解,最优解含有值为0的分量,因此为稀疏的解,计算速度快。
在结束本章前,观察在不同噪音情况下,参数 如何选择。目标函数设计成15次多项式函数,如图14-9表示固定确定性噪音,不同随机性噪音下,参数
如何选择。目标函数设计成15次多项式函数,如图14-9表示固定确定性噪音,不同随机性噪音下,参数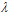 最佳选择,横坐标表示参数
最佳选择,横坐标表示参数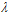 的选择,纵坐标表示
的选择,纵坐标表示 ,其中加粗的点表示在该种噪音情况下参数
,其中加粗的点表示在该种噪音情况下参数 的最佳取值。(此处因为是为了观察在不同噪音下如何选择参数
的最佳取值。(此处因为是为了观察在不同噪音下如何选择参数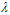 ,目标函数是已知的,所以可以求出
,目标函数是已知的,所以可以求出 ,现实中是不可能的,下一个例子也是如此,不再重复解释)
,现实中是不可能的,下一个例子也是如此,不再重复解释)

图14-9 不同随机性噪音下参数 的选择
的选择
目标函数设计成15次多项式函数,如图14-10表示固定随机性噪音,不同确定性噪音下,参数 最佳选择,横坐标表示参数
最佳选择,横坐标表示参数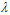 的选择,纵坐标表示
的选择,纵坐标表示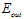 ,其中加粗的点表示在该种噪音情况下参数
,其中加粗的点表示在该种噪音情况下参数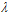 的最佳取值。
的最佳取值。
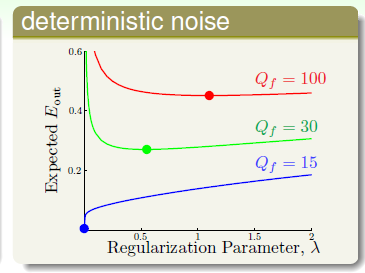
图14-10不同确定性噪音下参数 的选择
的选择
从上述两个图中不难得出,越大的噪音需要越大的正则化,这如同越颠簸的路,越需要踩刹车一样。但是一个更重要的问题却没有解决,即在噪音未知的情况下,如何选择参数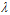 ,这是下章的内容。
,这是下章的内容。



