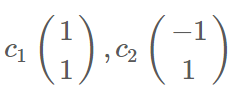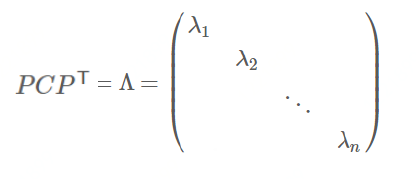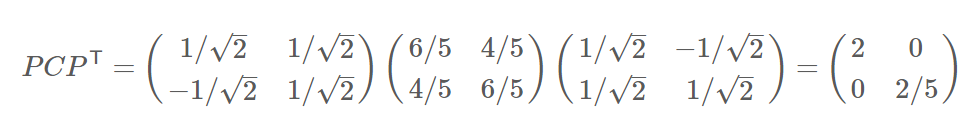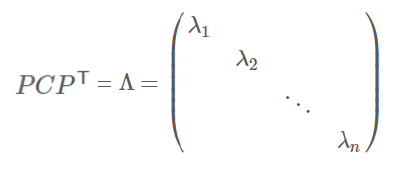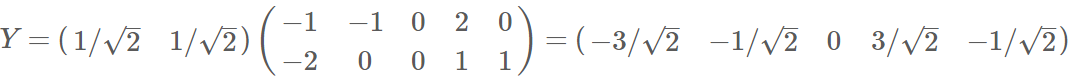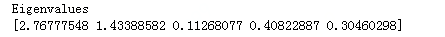基本概念:
在数据处理中,经常会遇到特征维度比样本数量多得多的情况,如果拿到实际工程中去跑,效果不一定好。一是因为冗余的特征会带来一些噪音,影响计算的结果;二是因为无关的特征会加大计算量,耗费时间和资源。所以我们通常会对数据重新变换一下,再跑模型。数据变换的目的不仅仅是降维,还可以消除特征之间的相关性,并发现一些潜在的特征变量。
PCA的目的:
PCA是一种在尽可能减少信息损失的情况下找到某种方式降低数据的维度的方法。通常来说,我们期望得到的结果,是把原始数据的特征空间(n个d维样本)投影到一个小一点的子空间里去,并尽可能表达的很好(就是说损失信息最少)。常见的应用在于模式识别中,我们可以通过减少特征空间的维度,抽取子空间的数据来最好的表达我们的数据,从而减少参数估计的误差。注意,主成分分析通常会得到协方差矩阵和相关矩阵。这些矩阵可以通过原始数据计算出来。协方差矩阵包含平方和与向量积的和。相关矩阵与协方差矩阵类似,但是第一个变量,也就是第一列,是标准化后的数据。如果变量之间的方差很大,或者变量的量纲不统一,我们必须先标准化再进行主成分分析。
PCA小实例步骤:
原始数据

协方差矩阵
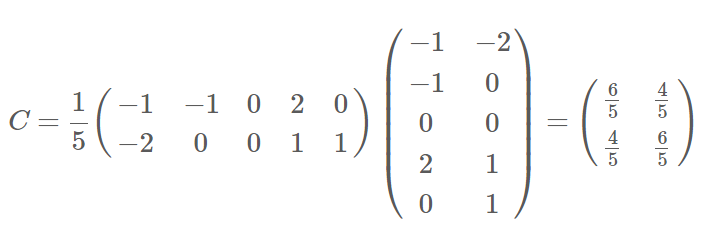
特征值 : 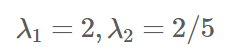 特征向量:
特征向量: 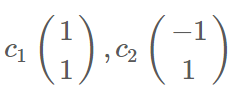
对角化 :
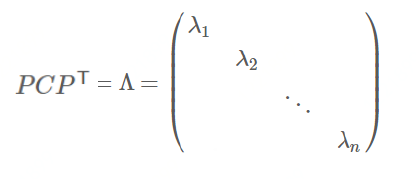
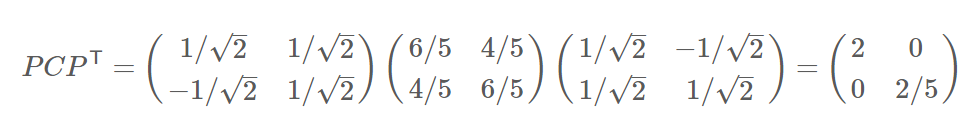
协方差矩阵对角化:即除对角线外的其它元素化为0,并且在对角线上
将元素按大小从上到下排列
协方差矩阵对角化:
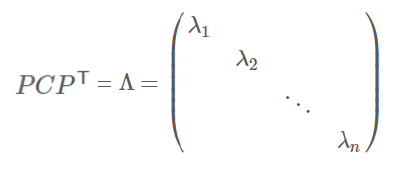
降维:
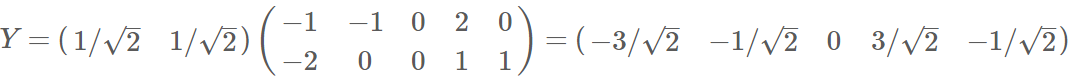
正文:
需求不同机器五个维度降维再做聚类,可分析离群机器。
import numpy as np
import pandas as pd
df = pd.read_csv('data2.csv')
df['lable'] = 'machine'
df.head()
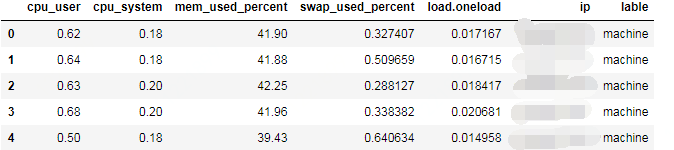
#X取前5列数据,y取label
X = df.ix[:,0:5].values
y = df.ix[:,6].values
from matplotlib import pyplot as plt
import math
#数据归一化处理
from sklearn.preprocessing import StandardScaler
X_std = StandardScaler().fit_transform(X)
print (X_std)

#构造协方差矩阵
mean_vec = np.mean(X_std, axis=0)
cov_mat = (X_std - mean_vec).T.dot((X_std - mean_vec)) / (X_std.shape[0]-1)
print(cov_mat)

#计算特征值和特征向量
cov_mat = np.cov(X_std.T)
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
print('Eigenvectors \n%s' %eig_vecs)
print('\nEigenvalues \n%s' %eig_vals)
特征向量如下 5x5矩阵:

特征值如下:
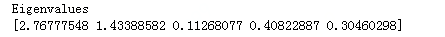
#把特征向量和特征值对应起来,为计算特征值权重。
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
print (eig_pairs)
print ('----------')
#按特征值排序,注意与原始数据无关
eig_pairs.sort(key=lambda x: x[0], reverse=True)
print('Eigenvalues in descending order:')
for i in eig_pairs:
print(i)

#对每个特征值对应的特征向量求累加和,分析特征值的权重
tot = sum(eig_vals)
var_exp = [(i / tot)*100 for i in sorted(eig_vals, reverse=True)]
print (var_exp)
cum_var_exp = np.cumsum(var_exp)
cum_var_exp

#可以看出前两个特征值的影响比较大,说明降成2维是比较合理的。当然降三维就更好一点,但是复杂度也相应提高了。
#对特征值权重可视化
plt.figure(figsize=(6, 4))
plt.bar(range(5), var_exp, alpha=0.5, align='center',
label='individual explained variance')
plt.step(range(5), cum_var_exp, where='mid',
label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')
plt.legend(loc='best')
plt.tight_layout()
plt.show()

#构造一个5 x 2矩阵
matrix_w = np.hstack((eig_pairs[0][1].reshape(5,1),
eig_pairs[1][1].reshape(5,1)))
print('Matrix W:\n', matrix_w)
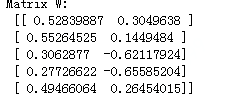
#降维,用原始矩阵乘以5x2矩阵
Y = X_std.dot(matrix_w)

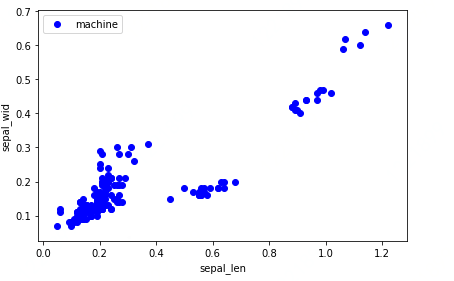
#未降维的可视化散点图
plt.figure(figsize=(6, 4))
for lab, col in zip(('machine',),
('blue', )):
plt.scatter(X[y==lab, 0],
X[y==lab, 1],
label=lab,
c=col)
plt.xlabel('sepal_len')
plt.ylabel('sepal_wid')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
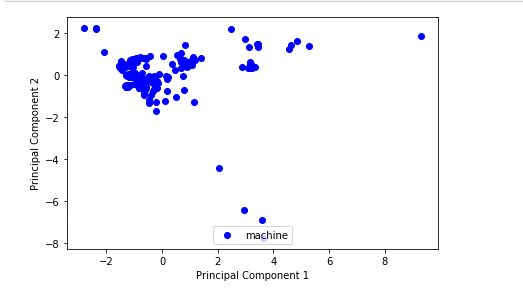
#降维后的散点图
plt.figure(figsize=(6, 4))
for lab, col in zip(('machine', ),
('blue',)):
plt.scatter(Y[y==lab, 0],
Y[y==lab, 1],
label =lab,
c=col,
)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.legend(loc='lower center')
plt.tight_layout()
plt.show()
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
对降维后的数据集用DBScan聚类
基本概念:
核心对象:若某个点的密度达到算法设定的阈值则其为核心点。(即r 邻域内点的数量不小于minPts)
直接密度可达:若某点p在点q的r 邻域内,且q是核心点则p-q直接密度可达。
密度可达:若有一个点的序列q0、q1、…qk,对任意qi-qi-1是直接密度可达的,则称从q0到qk密度可达,这实际上是直接密度可达的“传播”。
ϵ-邻域的距离阈值:设定的半径r
边界点:属于某一个类的非核心点,不能发展下线了
噪声点:不属于任何一个类簇的点,从任何一个核心点出发都是密度不可达的
工作流程:
参数D:输入数据集
参数ϵ:指定半径
MinPts:密度阈值
参数选择:
半径ϵ,可以根据K距离来设定:找突变点
K距离:给定数据集P={p(i); i=0,1,…n},计算点P(i)到集合D的子集S中所有点
之间的距离,距离按照从小到大的顺序排序,d(k)就被称为k-距离。
MinPts:k-距离中k的值,一般取的小一些,多次尝试
优势:
不需要指定簇个数
擅长找到离群点(检测任务)
可以发现任意形状的簇
两个参数就够了
劣势:
高维数据有些困难(可以做降维)
Sklearn中效率很慢(数据削减策略)
参数难以选择(参数对结果的影响非常大)
正文:
import numpy as np # 数据结构
import sklearn.cluster as skc # 密度聚类
from sklearn import metrics # 评估模型
db = skc.DBSCAN(eps=2.5, min_samples=2).fit(Y) #DBSCAN聚类方法 还有参数,matric = ""距离计算方法
labels = db.labels_ #和X同一个维度,labels对应索引序号的值 为她所在簇的序号。若簇编号为-1,表示为噪声
print('每个样本的簇标号:')
print(labels)
raito = len(labels[labels[:] == -1]) / len(labels) #计算噪声点个数占总数的比例
print('噪声比:', format(raito, '.2%'))
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0) # 获取分簇的数目
print('分簇的数目: %d' % n_clusters_)
print("轮廓系数: %0.3f" % metrics.silhouette_score(Y, labels)) #轮廓系数评价聚类的好坏
for i in range(n_clusters_):
print('簇 ', i, '的所有样本:')
one_cluster = Y[labels == i]
print(one_cluster)
plt.plot(one_cluster[:,0],one_cluster[:,1],'o')
plt.plot(Y[labels == -1][:,0],Y[labels == -1][:,1],'p')
plt.show()
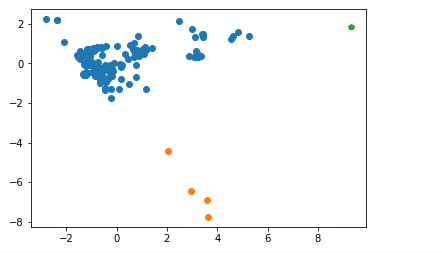
每个样本的簇标号:
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
噪声比: 0.54%
分簇的数目: 2
轮廓系数: 0.736
簇 0 的所有样本:
[[ 9.96854482e-01 6.19896578e-01]
[ 1.08138246e+00 4.71724901e-01]
[ 1.17571829e+00 7.00808757e-01]
[ 1.39995504e+00 7.96744932e-01]
[ 6.73080835e-01 3.19912177e-01]
[ 1.02590239e+00 6.68824085e-01]
[ 1.06530721e+00 7.07484773e-01]
[ 1.11189776e+00 8.39291101e-01]
[ 3.14722562e+00 3.27367426e-01]
[ 3.21549700e+00 3.24569658e-01]
[ 3.16082539e+00 4.44035187e-01]
[ 3.35548775e+00 3.73044767e-01]
[ 2.98229019e+00 1.72184325e+00]
[ 3.08645455e+00 3.42078565e-01]
[ 2.37094213e-02 8.72146114e-01]
[ 6.84628335e-01 6.30018499e-01]
[ 8.93515804e-01 3.86466713e-01]
[ 6.92034898e-01 1.05251158e+00]
[ 7.67477265e-01 6.83223943e-01]
[ 8.81635814e-01 5.87326858e-01]
[ 5.51545794e-01 9.57492502e-01]
[ 6.65530470e-01 7.47280594e-01]
[ 6.59982303e-01 7.30787717e-01]
[ 7.97399766e-01 6.88481483e-01]
[ 7.60785976e-01 -6.20768986e-02]
[ 1.15068696e+00 -1.28522051e+00]
[-1.01029051e-01 2.17385293e-02]
[ 4.55246274e-01 2.41142183e-01]
[-3.28463613e-01 -7.63226503e-01]
[ 1.08255376e-01 -1.26750744e+00]
[ 1.88234094e-01 -7.66753674e-01]
[ 7.81723172e-01 -7.03755924e-01]
[ 4.88350439e-01 -1.03386408e+00]
[-1.17478514e+00 4.32911156e-01]
[-6.00831989e-01 -2.49343240e-01]
[-6.76806838e-01 -3.18765479e-01]
[-4.11073705e-01 -9.41105284e-01]
[-8.62394297e-01 -2.85851329e-01]
[-7.93770724e-01 -2.41953487e-01]
[-6.24775559e-01 -2.78679115e-01]
[-5.81710593e-01 7.60832837e-01]
[-9.11707243e-01 6.16547904e-01]
[-8.65850835e-01 7.61228564e-01]
[-8.95841256e-01 7.25747391e-01]
[-2.97435552e-01 -6.63055497e-01]
[-6.69001053e-01 -3.02789798e-01]
[-7.10883112e-01 -2.37620685e-01]
[-5.96463645e-01 -3.73686091e-01]
[-1.04557102e+00 3.73146260e-01]
[-1.19140463e+00 5.71983742e-01]
[-2.37932735e+00 2.20144066e+00]
[-5.88125083e-01 -3.53114799e-01]
[-6.65952275e-01 -8.21979420e-01]
[-1.47101107e-01 -3.98421552e-01]
[-3.28115960e-01 -3.28822138e-01]
[ 1.71932280e-01 -1.84936809e-01]
[-2.11203864e-01 -1.30817031e+00]
[-2.13478421e-01 -1.74130561e+00]
[-4.65828329e-01 -1.35592284e+00]
[-4.70845360e-01 -1.22311301e+00]
[-6.16090086e-01 -4.31738814e-01]
[-8.40594427e-01 -3.54071331e-01]
[-9.97703877e-01 -4.26931248e-01]
[ 8.30405171e-01 1.40241740e+00]
[-1.56380804e+00 4.06810192e-01]
[-1.50387840e+00 4.51771017e-01]
[-1.44418161e+00 2.51771913e-01]
[-1.52901957e+00 4.22767721e-01]
[-1.46765387e+00 4.69984230e-01]
[-1.21729599e+00 -5.60195905e-01]
[-1.22599765e+00 -4.69268926e-01]
[-1.29160008e+00 -4.68647997e-01]
[-1.16770311e+00 -5.06891360e-01]
[-1.32733179e+00 -5.43739520e-01]
[-1.28797606e+00 -5.87222210e-01]
[-1.31184457e+00 -6.00027185e-01]
[-1.16723893e+00 -5.00196629e-01]
[ 5.25889754e+00 1.38681160e+00]
[ 4.83020633e+00 1.60052457e+00]
[ 2.88540988e+00 3.77353302e-01]
[ 3.16501658e+00 6.11262973e-01]
[ 3.20073856e+00 5.29818489e-01]
[ 3.13011049e+00 1.31522108e+00]
[-1.90442840e-01 -6.25108065e-01]
[-4.80266056e-01 -2.62477854e-01]
[-3.13268912e-01 -3.81018964e-01]
[-4.78508983e-01 -1.89609826e-01]
[-1.71396770e-01 -2.74308409e-01]
[ 2.01161735e-01 -9.36331840e-02]
[-2.73763626e-01 -2.42025105e-01]
[-3.39595861e-01 -1.95241273e-01]
[-4.30473172e-01 8.83471269e-01]
[-7.86812641e-01 8.54301623e-01]
[-6.23150134e-01 8.16906329e-01]
[-7.37928790e-01 7.77305066e-01]
[-3.85207757e-01 -3.47488032e-01]
[-2.76369410e-01 -5.47225197e-02]
[-2.62866587e-01 -2.47706939e-01]
[-4.05693574e-01 -1.33211603e-01]
[-1.06883370e+00 4.64087658e-01]
[-1.09822647e+00 6.46430738e-01]
[-2.37367370e+00 2.18477030e+00]
[-2.88973398e-01 -1.56221787e-01]
[-3.10411358e-01 -1.28697344e-01]
[-8.03671265e-01 -4.38452971e-01]
[-9.01509608e-01 -4.84502970e-01]
[-8.26746712e-01 -4.64530516e-01]
[-7.89727574e-01 -5.22936335e-01]
[-7.30479915e-01 -3.87994232e-01]
[-2.80043634e+00 2.23689253e+00]
[-5.68881745e-01 -6.51584309e-01]
[-7.82237337e-01 -4.51296126e-01]
[-7.36060324e-01 7.15270569e-02]
[-1.19768310e+00 -1.16800394e-01]
[-9.73380913e-01 6.59565280e-02]
[-1.12321350e+00 -9.67460101e-02]
[-1.06259743e+00 -8.27447208e-02]
[ 2.48644946e+00 2.15868772e+00]
[-1.45314882e+00 2.43476167e-01]
[-1.52641231e+00 3.11302328e-01]
[-1.33779156e+00 3.72097353e-01]
[-1.37873757e+00 4.89699573e-01]
[-1.37639570e+00 4.18616151e-01]
[-8.09774354e-01 -5.08058713e-01]
[-9.31131620e-01 -1.42751196e-01]
[-4.53649994e-01 -7.72097038e-02]
[-6.65236344e-01 -2.20065071e-01]
[-6.44250028e-01 -3.73374971e-01]
[-8.42391041e-01 -6.19906940e-01]
[ 1.32781239e-01 -5.22812674e-02]
[-8.10169381e-01 -6.26064995e-01]
[-5.72634711e-01 4.18058813e-01]
[-1.16497509e+00 7.24752982e-01]
[-1.07845985e+00 7.36963143e-01]
[-9.26271043e-01 7.81711660e-01]
[-5.90426126e-01 -6.05501838e-01]
[-8.26077963e-01 -1.53064233e-01]
[-7.92101529e-01 -1.04694572e-01]
[-7.06320482e-01 -2.54049986e-01]
[-1.46436457e+00 6.52207754e-01]
[-1.47064051e+00 5.13823003e-01]
[-2.08998281e+00 1.07339874e+00]
[-9.24745013e-01 -1.05378350e-01]
[-8.95026540e-01 -8.91345628e-02]
[-8.07888497e-01 -6.65654322e-02]
[-6.96084433e-01 -3.98815263e-01]
[-7.27744516e-01 -6.39194870e-01]
[-6.29664044e-01 -7.41390880e-01]
[-8.23277654e-01 -4.96035188e-01]
[-6.52040434e-01 -9.71113524e-01]
[ 4.63635478e+00 1.40947821e+00]
[ 4.55603278e+00 1.22052016e+00]
[ 3.39684550e+00 1.47199654e+00]
[ 3.43902228e+00 1.47032924e+00]
[ 3.44439952e+00 1.33884706e+00]
[ 3.43749952e-01 4.92195283e-01]
[ 8.93159103e-01 5.54338159e-01]
[ 7.86428912e-01 5.42368005e-01]
[ 7.67590916e-01 5.68011165e-01]
[ 7.83647530e-01 5.16254564e-01]
[ 8.11704348e-01 5.02071745e-01]
[ 7.77892641e-01 4.64009450e-01]
[ 8.75448669e-01 4.66897705e-01]
[ 7.38859628e-01 4.21602580e-01]
[-1.24757204e+00 -6.99340120e-02]
[-8.72636812e-01 -4.42551962e-01]
[-1.13063387e+00 -3.39702802e-02]
[-1.30316761e+00 -3.36274459e-02]
[-1.12978717e+00 9.41996543e-02]
[-1.31048184e+00 -1.88393972e-02]
[-1.05546107e+00 -4.26031697e-03]
[-1.23538597e+00 5.55172607e-02]
[-1.19462472e+00 1.43943069e-02]
[-1.05422060e+00 7.16215092e-02]
[-1.18828910e+00 1.54679147e-02]
[-1.24832171e+00 -3.30616363e-02]
[-1.20834955e+00 -2.89264455e-02]
[-1.12933915e+00 2.71400462e-02]
[-1.11865886e+00 3.30991112e-02]
[-1.20204568e+00 -9.82951013e-03]]
簇 1 的所有样本:
[[ 3.58349685 -6.91918766]
[ 3.62286913 -7.76192187]
[ 2.95477472 -6.43354311]
[ 2.02711371 -4.4162005 ]]

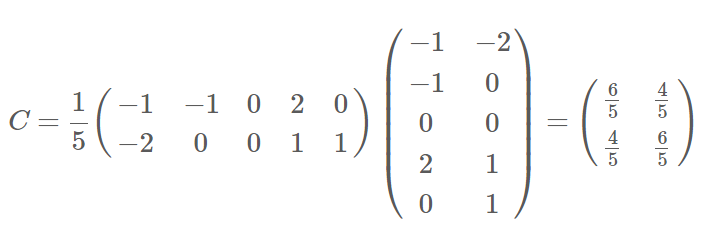
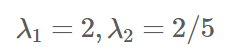 特征向量:
特征向量: