机器学习笔记(1)：线性回归

初次接触机器学习的朋友们，建议先把这篇概念性的科普文章，精读5遍以上：神经网络浅讲：从神经元到深度学习

下列代码来自 https://zh.gluon.ai/chapter_supervised-learning/linear-regression-scratch.html

里面有大量的矩阵向量的操作，不熟悉NDArray的，建议先看上一篇mxnet安装及NDArray初体验

下面这个示例的思路，先讲解一下，不然不知道它们在干嘛：）

先给出一个线性方程（1），如下图：

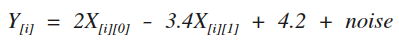
利用这个方程生成一堆数据集，然后再建立一个线性回归模型（2），如下图：

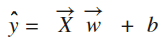
等价于下面这样：

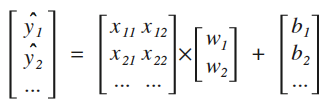
（注：上图中的b1 , b2 ... 其实相同）

再利用随机梯度下降法，进行迭代运算，计算预测值yhat，直到下面的损失函数

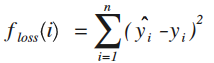
不断减小（即：收敛)，然后看看这时得到的参数w(是一个向星)以及偏置值b是否跟线性方程中设定的参数[2, -3.4]以及4.2相同，如果很接近，说明我们用深度学习算法，基于一堆数据成功预测出了想要的结果（即：线性回归成功），这种已知答案，利用一堆数据进行训练的学习方法，也称为有监督学习。

from mxnet import ndarray as nd
from mxnet import autograd
import random

num_inputs = 2
num_examples = 1000

true_w = [2, -3.4]
true_b = 4.2

X = nd.random_normal(shape=(num_examples, num_inputs)) #1000行，2列的数据集
y = true_w[0] * X[:, 0] + true_w[1] * X[:, 1] + true_b #已知答案的结果
y += .01 * nd.random_normal(shape=y.shape) #加入噪音

batch_size = 10
def data_iter():
    #产生一个随机索引列表
    idx = list(range(num_examples))
    random.shuffle(idx)
    for i in range(0, num_examples, batch_size):
        j = nd.array(idx[i:min(i+batch_size,num_examples)])
        yield nd.take(X, j), nd.take(y, j) #每次随机从X中取出10行数据，以及对应的结果y值

#初始化模型参数（即：需要求解的参数变量）
w = nd.random_normal(shape=(num_inputs, 1))
b = nd.zeros((1,))
params = [w, b]

#创建梯度
for param in params:
    param.attach_grad()
    
#定义线性回归模型
def net(X):
    return nd.dot(X, w) + b

#定义损失函数
def square_loss(yhat, y):
    # 注意这里我们把y变形成yhat的形状来避免自动广播
    return (yhat - y.reshape(yhat.shape)) ** 2

#随机梯度下降法
def SGD(params, lr):
    for param in params:
        param[:] = param - lr * param.grad
        

#训练
epochs = 5
learning_rate = .001
for e in range(epochs):
    total_loss = 0
    for data, label in data_iter():
        with autograd.record():
            output = net(data)
            loss = square_loss(output, label)
        loss.backward()
        SGD(params, learning_rate)

        total_loss += nd.sum(loss).asscalar()
    print("Epoch %d, average loss: %f" % (e, total_loss/num_examples))

print(true_w) #打印答案
print(w) #打印求解结果

print(true_b) #打印答案
print(b) #打印求解结果

Epoch 0, average loss: 6.012281
Epoch 1, average loss: 0.102830
Epoch 2, average loss: 0.001909
Epoch 3, average loss: 0.000133
Epoch 4, average loss: 0.000101 #5次迭代后，已经快速收敛
[2, -3.4] #已知答案

[[ 2.00017834] #求解结果
 [-3.40006614]]
<NDArray 2x1 @cpu(0)>
4.2

[ 4.19863892]
<NDArray 1 @cpu(0)>