javascript:算法笔记
入门级算法-线性查找-时间复杂度O(n)--相当于算法界中的HelloWorld
//线性搜索(入门HelloWorld)
//A为数组，x为要搜索的值
function linearSearch(A, x) {
for (var i = 0; i < A.length; i++) {
if (A[i] == x) {
return i;
}
}
return -1;
}
二分查找(又称折半查找) - 适用于已排好序的线性结构 - 时间复杂度O(logN)
//二分搜索
//A为已按"升序排列"的数组，x为要查询的元素
//返回目标元素的下标
function binarySearch(A, x) {
var low = 0, high = A.length - 1;
while (low <= high) {
var mid = Math.floor((low + high) / 2); //下取整
if (x == A[mid]) {
return mid;
}
if (x < A[mid]) {
high = mid - 1;
}
else {
low = mid + 1;
}
}
return -1;
}
冒泡排序 -- 时间复杂度O(n^2)
//冒泡排序
function bubbleSort(A) {
for (var i = 0; i < A.length; i++) {
var sorted = true;
//注意：内循环是倒着来的
for (var j = A.length - 1; j > i; j--) {
if (A[j] < A[j - 1]) {
swap(A, j, j - 1);
sorted = false;
}
}
if (sorted) {
return;
}
}
}
选择排序 -- 时间复杂度O(n^2)
//选择排序
//思路：找到最小值的下标记下来，再交换
function selectionSort(A) {
for (var i = 0; i < A.length - 1; i++) {
var k = i;
for (var j = i + 1; j < A.length; j++) {
if (A[j] < A[k]) {
k = j;
}
}
if (k != i) {
var t = A[k];
A[k] = A[i];
A[i] = t;
println(A);
}
}
return A;
}
插入排序 -- 时间复杂度O(n^2)
//插入排序
//假定当前元素之前的元素已经排好序，先把自己的位置空出来，
//然后前面比自己大的元素依次向后移，直到空出一个"坑"，
//然后把目标元素插入"坑"中
function insertSort(A) {
for (var i = 1; i < A.length; i++) {
var x = A[i];
for (var j = i - 1; j >= 0 && A[j] > x; j--) {
A[j + 1] = A[j];
}
if (A[j + 1] != x) {
A[j + 1] = x;
println(A);
}
}
return A;
}
字符串反转 -- 时间复杂度O(logN)
//字符串反转(比如：ABC -> CBA)
function inverse(s) {
var arr = s.split('');
var i = 0, j = arr.length - 1;
while (i < j) {
var t = arr[i];
arr[i] = arr[j];
arr[j] = t;
i++;
j--;
}
return arr.join('');
}
关于稳定性排序的一个结论：
基于比较的简单排序算法，即时间复杂度为O(N^2)的排序算法，通常可认为均是稳定排序
其它先进的排序算法，比如归并排序、堆排序、桶排序之类（通常这类算法的时间复杂度可优化为n*LogN），通常可认为均是不稳定排序
单链表实现
<script type="text/javascript">
function print(msg) {
document.write(msg);
}
function println(msg) {
print(msg + "<br/>");
}
//节点类
var Node = function (v) {
this.data = v; //节点值
this.next = null; //后继节点
}
//单链表
var SingleLink = function () {
this.head = new Node(null); //约定头节点仅占位，不存值
//插入节点
this.insert = function (v) {
var p = this.head;
while (p.next != null) {
p = p.next;
}
p.next = new Node(v);
}
//删除指定位置的节点
this.removeAt = function (n) {
if (n <= 0) {
return;
}
var preNode = this.getNodeByIndex(n - 1);
preNode.next = preNode.next.next;
}
//取第N个位置的节点(约定头节点为第0个位置)
//N大于链表元素个数时，返回最后一个元素
this.getNodeByIndex = function (n) {
var p = this.head;
var i = 0;
while (p.next != null && i < n) {
p = p.next;
i++;
}
return p;
}
//查询值为V的节点，
//如果链表中有多个相同值的节点，
//返回第一个找到的
this.getNodeByValue = function (v) {
var p = this.head;
while (p.next != null) {
p = p.next;
if (p.data == v) {
return p;
}
}
return null;
}
//打印输出所有节点
this.print = function () {
var p = this.head;
while (p.next != null) {
p = p.next;
print(p.data + " ");
}
println("");
}
}
//测试单链表L中是否有重复元素
function hasSameValueNode(singleLink) {
var i = singleLink.head;
while (i.next != null) {
i = i.next;
var j = i;
while (j.next != null) {
j = j.next;
if (i.data == j.data) {
return true;
}
}
}
return false;
}
//单链表元素反转
function reverseSingleLink(singleLink) {
var arr = new Array();
var p = singleLink.head;
//先跑一遍，把所有节点放入数组
while (p.next != null) {
p = p.next;
arr.push(p.data);
}
var newLink = new SingleLink();
//再从后向前遍历数组,加入新链表
for (var i = arr.length - 1; i >= 0; i--) {
newLink.insert(arr[i]);
}
return newLink;
}
var linkTest = new SingleLink();
linkTest.insert('A');
linkTest.insert('B');
linkTest.insert('C');
linkTest.insert('D');
linkTest.print();//A B C D
var newLink = reverseSingleLink(linkTest);
newLink.print();//D C B A
</script>
-----------------------------
关于邻接矩阵、邻接表的选择：
邻接矩阵、邻接表都是图的基本存储方式，
稀松图情况下（即边远小于顶点情况下），用邻接表存储比较适合（相对矩阵N*N而言，邻接表只存储有值的边、顶点，不存储空值，存储效率更高）
稠密图情况下（即边远大地顶点情况下），用邻接矩阵存储比较适合（数据较多的情况下，要对较做遍历，如果用链表存储，要经常跳来跳去，效率较低）
-----------------------
堆：
几乎完全的二叉树：除了最右边位置上的一个或几个叶子可能缺少的二叉树。在物理存储上，可以用数组来存储，如果A[j]的顶点有左、右子节点，则左节点为A[2j]、右节点为A[2j+1]，A[j]的父顶点存储在A[j/2]中
堆：本身是一颗几乎完全的二叉树，而且父节点的值不小于子节点的值。应用场景：优先队列，寻找最大或次最大值；以及把一个新元素插入优先队列。
注：以下所有讨论的堆，约定索引0处的元素仅占位，有效元素从下标1开始
根据堆的定义，可以用以下代码测试一个数组是否为堆：
//测试数组H是否为堆
//(约定有效元素从下标1开始)
//时间复杂度O(n)
function isHeap(H) {
if (H.length <= 1) { return false; }
var half = Math.floor(H.length / 2); //根据堆的性质，循环上限只取一半就够了
for (var i = 1; i <= half; i++) {
//如果父节点，比任何一个子节点 小，即违反堆定义
if (H[i] < H[2 * i] || H[i] < H[2 * i + 1]) {
return false;
}
}
return true;
}
节点向上调整siftUp
某些情况下，如果堆中的某个元素值改变后(比如 10,8,9,7 变成 10,8,9,20 后，20需要向上调整 )，不再满足堆的定义，需要向上调整时，可以用以下代码实现
//堆中的节点上移
//(约定有效元素从下标1开始)
function siftUp(H, i) {
if (i <= 1) {
return;
}
for (var j = i; j > 1; j = Math.floor(j / 2)) {
var k = Math.floor(j / 2);
//发现 子节点 比 父节点大，则与父节点交换位置
if (H[j] > H[k]) {
var t = H[j];
H[j] = H[k];
H[k] = t;
}
else {
//说明已经符合堆定义，调整结束，退出
return;
}
}
}
节点向下调整siftDown (既然有向上调整，自然也有向下调整)
//堆中的节点下移
//(约定有效元素从下标1开始)
//时间复杂度O(logN)
function siftDown(H, i) {
if (2 * i > H.length) { //叶子节点，就不用再向下移了
return;
}
for (var j = 2 * i; j < H.length; j = 2 * j) {
//将j定位到 二个子节点中较大的那个上(很巧妙的做法)
if (H[j + 1] > H[j]) {
j++;
}
var k = Math.floor(j / 2);
if (H[k] < H[j]) {
var t = H[k];
H[k] = H[j];
H[j] = t;
}
else {
return;
}
}
}
向堆中添加新元素
//向堆H中添加元素x
//时间复杂度O(logN)
function insert(H, x) {
//思路：先在数组最后加入目标元素x
H.push(x);
//然后向上推
siftUp(H, H.length - 1);
}
从堆中删除元素
//删除堆H中指定位置i的元素
//时间复杂度O(logN)
function remove(H, i) {
//思路：先把位置i的元素与最后位置的元素n交换
//然后数据长度减1(这样就把i位置的元素给干掉了，但是整个堆就被破坏了)
//需要做一个决定：最后一个元素n需要向上调整，还是向下调整
//依据：比如比原来该位置的元素大，则向上调整，反之向下调整
var x = H[i]; //先把原来i位置的元素保护起来
//把最后一个元素放到i位置
//同时删除最后一个元素(js语言的优越性体现!)
H[i] = H.pop();
var n = H.length - 1;
if (i == n + 1) {
//如果去掉的正好是最后二个元素之一，
//无需再调整
return ;
}
if (H[i] > x) {
siftUp(H, i);
}
else {
siftDown(H, i);
}
}
//从堆中删除最大项
//返回最大值
//时间复杂度O(logN)
function deleteMax(H) {
var x = H[1];
remove(H, 1);
return x;
}
堆排序：
这是一种思路非常巧妙的排序算法，精华在于充分利用了“堆”这种数据结构本身的特点（首元素必然最大），而且每个元素的上移、下调，时间复试度又比较低，仅为O(logN)，空间上，也无需借助额外的存储空间，仅在数组自身内部交换元素即可。
思路：
1、先将首元素(即最大元素)与最末尾的元素对调---目的在于，把最大值沉底，下一轮重就不再管它了
2、经过1后，剩下的元素通常已经不再是一个堆了。这时，只要把新的首元素用siftDown下调，调整完以后，新的最大值元素自然又上升到了首元素的位置
3、反复1、2，大的元素逐一沉底，最后整个数组就有序了。
时间复杂度分析：创建堆需要O(n)的代价，每次siftDown代价为O(logN)，最多调整n-1个元素，所以总代价为 O(N) + (N-1)O(logN)，最终时间复杂度为O(NLogN)
//堆中的节点下移
//(约定有效元素从下标1开始)
//i为要调整的元素索引
//n为待处理的有效元素下标范围上限值
//时间复杂度O(logN)
function siftDown(H, i, n) {
if (n >= H.length) {
n = H.length;
}
if (2 * i > n) { //叶子节点，就不用再向下移了
return;
}
for (var j = 2 * i; j < n; j = 2 * j) {
//将j定位到 二个子节点中较大的那个上(很巧妙的做法)
if (H[j + 1] > H[j]) {
j++;
}
var k = Math.floor(j / 2);
if (H[k] < H[j]) {
var t = H[k];
H[k] = H[j];
H[j] = t;
}
else {
return;
}
}
}
//对数组的前n个元素进行创建堆的操作
function makeHeap(A, n) {
if (n >= A.length) {
n = A.length;
}
for (var i = Math.floor(n / 2); i >= 1; i--) {
siftDown(A, i, n);
}
}
//堆排序(非降序排列)
//时间复杂度O(nlogN)
function heapSort(H) {
//先建堆
makeHeap(H, H.length);
for (var j = H.length - 1; j >= 2; j--) {
//首元素必然是最大的
//将最大元素与最后一个元素互换，
//即将最大元素沉底，下一轮不再考虑
var x = H[1];
H[1] = H[j];
H[j] = x;
//互换后，剩下的元素不再满足堆定义，
//把新的首元素下调(以便继续维持堆的"形状")
//调整完后，剩下元素中的最大值必须又浮到了第一位
//进入下一轮循环
siftDown(H, 1, j - 1);
}
return H;
}
关于建堆，如果明白其中的原理后，也可以逆向思路，反过来做
function makeHeap2(A, n) {
if (n >= A.length) {
n = A.length;
}
for (var i = Math.floor(n / 2); i <= n; i++) {
siftUp(A, i);
}
}
--------------------------
不相交集合查找、合并
//定义节点Node类
var Node = function (v, p) {
this.value = v; //节点的值
this.parent = p; //节点的父节点
this.rank = 0; //节点的秩(默认为0)
}
//查找包含节点x的树根节点
var find = function (x) {
var y = x;
while (y.parent != null) {
y = y.parent;
}
var root = y;
y = x;
//沿x到根进行“路径压缩”
while (y.parent != null) {
//先把父节点保存起来，否则下一行调整后，就弄丢了
var w = y.parent;
//将目标节点挂到根下
y.parent = root;
//再将工作指针，还原到 目标节点原来的父节点上，
//继续向上逐层压缩
y = w
}
return root;
}
//合并节点x，y对应的两个树
//时间复杂度O(m) - m为待合并的子集合数量
var union = function (x, y) {
//先找到x所属集合的根
var u = find(x);
//再找到y所属集合的根
var v = find(y);
//把rank小的集合挂到rank大的集合上
if (u.rank <= v.rank) {
u.parent = v;
if (u.rank == v.rank) {
//二个集合的rank不分伯仲时
//给"胜"出方一点奖励，rank+1
v.rank += 1;
}
}
else {
v.parent = u;
}
}
归纳法：
先来看二个排序的递归实现
//选择排序的递归实现
//调用示例: selectionSort([3,2,1],0)
function selectionSortRec(A, i) {
var n = A.length - 1;
if (i < n) {
var k = i;
for (var j = i + 1; j <= n; j++) {
if (A[j] < A[k]) {
k = j
}
}
if (k != i) {
var t = A[k];
A[k] = A[i];
A[i] = t;
}
selectionSortRec(A, i + 1);
}
}
//插入排序递归实现
//调用示例:insertSortRec([4,3,2,1],3);
function insertSortRec(A, i) {
if (i > 0) {
var x = A[i];
insertSortRec(A, i - 1);
var j = i - 1;
while (j >= 0 && A[j] > x) {
A[j + 1] = A[j];
j--;
}
A[j + 1] = x;
}
}
递归的程序通常易于理解，代码也容易实现，再来看二个小例子：
从数组中，找出最大值
//在数组中找最大值(递归实现)
function findMax(A, i) {
if (i == 0) {
return A[0];
}
var y = findMax(A, i - 1);
var x = A[i - 1];
return y > x ? y : x;
}
var A = [1,2,3,4,5,6,7,8,9];
var test = findMax(A,A.length);
alert(test);//返回9
有一个已经升序排序好的数组，检查数组中是否存在二个数，它们的和正好为x ？
//5.33 递归实现
//A为[1..n]已经排好序的数组
//x为要测试的和
//如果存在二个数的和为x，则返回true，否则返回false
function sumX(A, i, j, x) {
if (i >= j) {
return false;
}
if (A[i] + A[j] == x) {
return true;
}
else if (A[i] + A[j] < x) {
//i后移
return sumX(A, i + 1, j, x);
}
else {
//j前移
return sumX(A, i, j - 1, x);
}
}
var A = [1, 2, 3, 4, 5, 6, 7, 8];
var test1 = sumX(A,0,A.length-1,9);
alert(test1); //返回true
递归程序虽然思路清晰，但通常效率不高，一般来讲，递归实现，都可以改写成非递归实现，上面的代码也可以写成：
//5.33 非递归实现
function sumX2(A, x) {
var i = 0, j = A.length - 1;
while (i < j) {
if (A[i] + A[j] == x) {
return true;
}
else if (A[i] + A[j] < x) {
//i后移
i++;
}
else {
//j前移
j--;
}
}
return false;
}
var A = [1, 2, 3, 4, 5, 6, 7, 8];
var test2 = sumX2(A,9);
alert(test2);//返回true
递归并不总代表低效率，有些场景中，递归的效率反而更高，比如计算x的m次幂，常规算法，需要m次乘法运算，下面的算法，却将时间复杂度降到了O(logn)
//计算x的m次幂（递归实现）
//时间复杂度O(logn)
function expRec(x, m) {
if (m == 0) {
return 1;
}
var y = expRec(x, Math.floor(m / 2));
y = y * y;
if (m % 2 != 0) {
y = x * y
}
return y;
}
当然，这其中并不光是递归的功劳，其效率的改进 主要依赖于一个数学常识： x^m = [x^(m/2)]^2，关于这个问题，还有一个思路很独特的非递归解法，巧妙的利用了二进制的特点
//将10进制数转化成2进制
function toBin(dec) {
var bits = [];
var dividend = dec;
var remainder = 0;
while (dividend >= 2) {
remainder = dividend % 2;
bits.push(remainder);
dividend = (dividend - remainder) / 2;
}
bits.push(dividend);
bits.reverse();
return bits.join("");
}
//计算x的m次幂（非递归实现）
//很独特的一种解法
function exp(x, m) {
var y = 1;
var bin = toBin(m).split('');
//先将m转化成2进制形式
for (var j = 0; j < bin.length; j++) {
y = y * 2;
//如果2进制的第j位是1，则再*x
if (bin[j] == "1") {
y = x * y
}
}
return y;
}
//println(expRec(2, 5));
//println(exp(2, 5));
再来看看经典的多项式求值问题：
给定一串实数An，An-1，...，A1，A0 和一个实数X，计算多项式Pn(x)的值
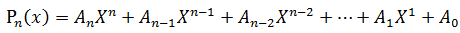
著名的Horner公式：
已经如何计算：
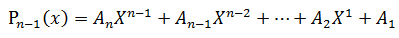
显然有：
这样只需要 N次乘法+N次加法
//多项式求值
//N次乘法+N次加法搞定，伟大的改进！
function horner(A, x) {
var n = A.length - 1
var p = A[n];
for (var j = 0; j < n; j++) {
p = x * p + A[n - j - 1];
}
return p;
}
//计算: y(2) = 3x^3 + 2x^2 + x -1;
var A = [-1, 1, 2, 3];
var y = horner(A, 2);
alert(y);//33
多数问题：
一个元素个数为n的数组，希望快速找出其中大于出现次数>n/2的元素（该元素也称为多数元素）。通常可用于选票系统，快速判定某个候选人的票数是否过半。最优算法如下：
//找出数组A中“可能存在”的多数元素
function candidate(A, m) {
var count = 1, c = A[m], n = A.length - 1;
while (m < n && count > 0) {
m++;
if (A[m] == c) {
count++;
}
else {
count--;
}
}
if (m == n) {
return c;
}
else {
return candidate(A, m + 1);
}
}
//寻找多数元素
//时间复杂度O(n)
function majority(A) {
var c = candidate(A, 0);
var count = 0;
//找出的c，可能是多数元素，也可能不是，
//必须再数一遍，以确保结果正确
for (var i = 0; i < A.length; i++) {
if (A[i] == c) {
count++;
}
}
//如果过半，则确定为多数元素
if (count > Math.floor(A.length / 2)) {
return c;
}
return null;
}
var m = majority([3, 2, 3, 3, 4, 3]);
alert(m);
以上算法基于这样一个结论：在原序列中去除两个不同的元素后，那么在原序列中的多数元素在新序列中还是多数元素
证明如下：
如果原序列的元素个数为n，多数元素出现的次数为x，则 x/n > 1/2
去掉二个不同的元素后，
a)如果去掉的元素中不包括多数元素，则新序列中 ，原先的多数元素个数/新序列元素总数 = x/(n-2) ，因为x/n > 1/2 ，所以 x/(n-2) 也必然>1/2
b)如果去掉的元素中包含多数元素，则新序列中 ，原先的多数元素个数/新序列元素总数 = (x-1)/(n-2) ，因为x/n > 1/2 =》 x>n/2 代入 (x-1)/(n-2) 中，
有 (x-1)/(n-2) > (n/2 -1)/(n-2) = 2(n-2)/(n-2) = 1/2
下一个问题：全排列
function swap(A, i, j) {
var t = A[i];
A[i] = A[j];
A[j] = t;
}
function println(msg) {
document.write(msg + "<br/>");
}
//全排列算法
function perm(P, m) {
var n = P.length - 1;
if (m == n) {
//完成一个新排列时，输出
println(P);
return;
}
for (var j = m; j <= n; j++) {
//将起始元素与后面的每个元素交换
swap(P, j, m);
//在前m个元素已经排好的基础上
//再加一个元素进行新排列
perm(P, m + 1);
//把j与m换回来，恢复递归调用前的“现场"，
//否则因为递归调用前，swap已经将原顺序破坏了，
//导致后面生成排序时，可能生成重复
swap(P, j, m);
}
}
perm([1, 2, 3], 0);
//1,2,3
//1,3,2
//2,1,3
//2,3,1
//3,2,1
//3,1,2
------------------------
分治法：
要点：将问题划分成二个子问题时，尽量让子问题的规模大致相等。这样才能最大程度的体现一分为二，将问题规模以对数折半缩小的优势。
//打印输出(调试用)
function println(msg) {
document.write(msg + "<br/>");
}
//数组中i,j位置的元素交换(辅助函数)
function swap(A, i, j) {
var t = A[i];
A[i] = A[j];
A[j] = t;
}
//寻找数组A中的最大、最小值(分治法实现)
function findMinMaxDiv(A, low, high) {
//最小规模子问题的解
if (high - low == 1) {
if (A[low] < A[high]) {
return [A[low], A[high]];
}
else {
return [A[high], A[low]];
}
}
var mid = Math.floor((low + high) / 2);
//在前一半元素中寻找子问题的解
var r1 = findMinMaxDiv(A, low, mid);
//在后一半元素中寻找子问题的解
var r2 = findMinMaxDiv(A, mid + 1, high);
//把二部分的解合并
var x = r1[0] > r2[0] ? r2[0] : r1[0];
var y = r1[1] > r2[1] ? r1[1] : r2[1];
return [x, y];
}
var r = findMinMaxDiv([1, 2, 3, 4, 5, 6, 7, 8], 0, 7);
println(r); //1,8
//二分搜索(分治法实现)
//输入：A为已按非降序排列的数组
//x 为要搜索的值
//low,high搜索的起、止索引范围
//返回：如果找到，返回下标，否则返回-1
function binarySearchDiv(A, x, low, high) {
if (low > high) {
return -1;
}
var mid = Math.floor((low + high) / 2);
if (x == A[mid]) {
return mid;
}
else if (x < A[mid]) {
return binarySearchDiv(A, x, low, mid - 1);
}
else {
return binarySearchDiv(A, x, mid + 1, high);
}
}
var f = binarySearchDiv([1, 2, 3, 4, 5, 6, 7], 4, 0, 6);
println(f); //3
//将数组A，以low位置的元素为界，划分为前后二半
//n为待处理的索引范围上限
function split(A, low, n) {
if (n >= A.length - 1) {
n = A.length - 1;
}
var i = low;
var x = A[low];
//二个指针一前一后“跟随”，
//最前面的指针发现有元素比分界元素小时，换到前半部
//后面的指针再紧跟上，“夫唱妇随”一路到头
for (var j = low + 1; j <= n; j++) {
if (A[j] <= x) {
i++;
if (i != j) {
swap(A, i, j);
}
}
}
//经过上面的折腾后，除low元素外，其它的元素均以就位
//最后需要把low与最后一个比low位置小的元素交换，
//以便把low放在分水岭位置上
swap(A, low, i);
return [A, i];
}
var A = [5, 1, 2, 6, 3];
var b = split(A, 0, A.length - 1);
println(b[0]); //3,1,2,5,6
//快速排序
function quickSort(A, low, high) {
var w = high;
if (low < high) {
var t = split(A, low, w); //分治思路，先分成二半
w = t[1];
//在前一半求解
quickSort(A, low, w - 1);
//在后一半求解
quickSort(A, w + 1, high);
}
}
var A = [5, 6, 4, 7, 3];
quickSort(A, 0, A.length - 1);
println(A); //3,4,5,6,7
split算法的思想应用：
设A[1..n]是一个整数集，给出一算法重排数组A中元素，使得所有的负整数放到所有非负整数的左边，你的算法的运行时间应当为Θ(n)
function sort1(A) {
var i = 0, j = A.length - 1;
while (i < j) {
if (A[i] >= 0 && A[j] >= 0) {
j--;
}
else if (A[i] < 0 && A[j] < 0) {
i++;
}
else if (A[i] > 0 && A[j] < 0) {
swap(A, i, j);
i++;
j--;
}
else {
i++;
j--;
}
}
}
function sort2(A) {
if (A.length <= 1) { return; }
var i = 0;
for (var j = i + 1; j < A.length; j++) {
if (A[j] < 0 && A[i] >= 0) {
swap(A, i, j);
i++;
}
}
}
var a = [1, -2, 3, -4, 5, -6, 0];
sort1(a);
println(a);//-6,-2,-4,3,5,1,0
var b = [1, -2, 3, -4, 5, -6, 0];
sort2(b);
println(b);//-2,-4,-6,1,5,3,0
未完待续...
作者：菩提树下的杨过
出处：http://yjmyzz.cnblogs.com
本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。
出处：http://yjmyzz.cnblogs.com
本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。
