斐波那契数列

斐波那契数列如下：

　　　　1，2，3，5，8，13，21，34，……

　　　　如果设F(n）为该数列的第n项（n∈N*），那么这句话可以写成如下形式：

　　　　F(n)=F(n-1)+F(n-2)

通项公式如下：

　　　　

 

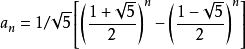
递归实现：

　　　　直接按照递推公式实现，

　　　　由通项公式可以得到：当n趋近于无穷大时

　　　　　　　　　　　　　　

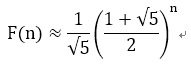
　　　　由于T(n)≥F(n)，这是一个指数阶的算法

　　　　如果我们今年计算出了F(100)，那么明年才能算出F(101)，

　　　　爆炸增量函数是算法设计的噩梦。

int fib(int n)
{
    if( n < 1)
        return -1;
    if( n == 1 || n == 2)
        return 1;
    return fib( n-1) + fib( n-2);
}

 数组优化：

　　　　既然斐波那契数列中的每一项是前两项之和，如果记录前两项的值，只需

　　　　要一次加法运算就可以得到当前项，那么可以使用数组。复杂度为O(n)。

int fib( int n)
{
    if( n < 1)
        return -1;
    int *a = new int [n];
    a[1] = a[2] = 1;
    for( int i = 3; i <= n; i++)
        a[i] = a[i-1]+a[i-2];
    return a[n];
}

 迭代法：

　　　　其实只需要得到第n个斐波那契数，中间结果只是为了下一次使用，不需要

　　　　记录，因此可以采用迭代法进行设计。使用若干辅助变量，迭代辗转相

　　　　加，每次记录前一项，时间复杂度为O(n)，空间复杂度降到O(1)。

int fib( int n)
{
    int i, s1, s2;
    if( n < 1)
        return -1;
    if( n == 1 || n == 2)
        return 1;
    s1 = s2 = 1;
    for( i = 3; i <= n; i++)
    {
        s2 = s1+s2;
        s1 = s2-s1;
    }
    return s2;
}

对数阶：

　　　　实质上，斐波那契数列时间复杂度还可以进一步降低到对数阶O(logⁿ)。

　　　　我们每次递归都将a+b的值赋给a,把a的值赋给b，通过观察可以发现,从1和

　　　　0开始将规则反复应用n次，将产生一对数fib(n)和fib(n+1),

　　　　现在将这种规则看成a = bq + aq + a*pb = bp + aq,其中p=0,q=1。把这种变

　　　　换称为T变换,Tpq 变换有个特性是 ：

　　　　Tpq 的二次方等于Tp'q', p' = pp + qq'q' = 2pq + q*q。

　　　　即：a = (bp+aq)p+(bq+aq+ap)q+(bq+aq+ap)p

　　　　　　   = b(2pq+q^2)+a(p^2+2pq+2q^2)

　　　　　　b = (bp+aq)p+(bq+aq+ap)q = b(p^2+q^2)+a(q^2+2pq)
　　　　此处p=0，q=1

int fib_iter( int a, int b, int count)
{
    if( count == 0)
        return b;
    return fib_iter( a+b, a, count-1);
}
int fib( int n)
{
    return fib_iter( 1, 0, n);
}