快速指数算法 和 求逆元算法
快速指数算法 和 求逆元 的算法是加密中常用到的两个算法。
这两个算法主要都是涉及到的 模运算 ,对于模运算的性质总结如下:
(1) (a + b) % n = (a % n + b % n) % n
(2) (a - b) % n = (a % n - b % n) % n
(3) (a * b) % n = (a % n * b % n) % n
(4) ab % n = ((a % n)b) % n
(1)式证明
∵ a = k1*n + r1
b = k2*n + r2
a % n = r1
b % n = r2
∴(a+b) % n = ((k1+k2)*n + (r1+r2)) % n = (r1+r2) % n = (a % n + b % n)% n
得证
(2)式证明同上
(3)式证明
a = k1*n + r1
b = k2*n + r2
(a*b) % n = (k1k2n2 + (k1r2+k2r1)n + r1r2) % n = r1r2 % n = (a %n * b %n ) % n
(4)式证明
设 a % n = r
ab %n= (a * a * a * a…*a) %n = (a %n * a %n * a %n * … * a %n) %n = rb % n = ((a % n) b) % n
快速指数算法: 要计算x的e次方对m取余的值,如果直接计算会数值会比较大,可以利用上面的模的性质进行降幂计算。
要计算 xe%m 的值 如 6265% 133 可以用如下的方法:
6265 % 133
= 62 * 6264 % 133
= 62 * (622)32 % 133
= 62 * 384432 % 133
= 62 * (3844 % 133)32 % 133
= 62 * 12032% 133
= 62 * 3616 % 133
= 62 * 998 % 133
= 62 * 924 % 133
= 62 * 852 % 133
= 62 * 43 % 133
= 2666 % 133
= 6
C# 中实现如下:
 View Code
View Code
public static int GetRemainder(int baseNum, int power, int modelNum)
{
//判断各个值正确性
int tempNum = 1;
int remainder = 0;
while (power >= 1)
{
//当为1的时候,得出结果
if (power == 1)
{
remainder = (tempNum * baseNum) % modelNum;
break;
}
else
{
//如果指数是偶数,将基数平方,指数除以2
if ((power&1)==0)
{
baseNum = (baseNum * baseNum) % modelNum;
power>>=1;
}
//如果是奇数,将tempNum乘以基数 并取模,指数减1
else
{
tempNum = (tempNum*baseNum)%modelNum;
power -= 1;
}
}
PrintProcess(baseNum, power, modelNum, tempNum);
}
return remainder;
}
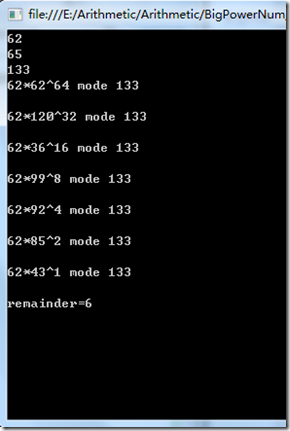
输入62、65、133测试数据输出结果如上图。
求逆元算法:
定义 如果ab≡1(mod m), 则称b是a的模m逆,记作a的模m逆是方程ax≡1(mod m)的解. 两个数互质一定有逆元。
求逆元可以使用辗转相除法,但是只有两个数都是质数的时候才有逆元,举例如下:
例:求5的模7逆
做辗转相除法, 求得整数b,k使得 5b+7k=1, 则b是5的模7逆.
计算如下:
7=5+2, 5=2×2+1.
回代 1=5-2×2=5-2×(7-5)= 3×5-2×7,
得 5 -1≡3(mod7).
例:求21的模73逆
做辗转相除法, 求得整数b,k使得 21b+73k=1, 则b是21的模73逆.
计算如下:
73=21*3+10
21=10*2+1
回代 1=21-10*2
1=21-(73-21*3)*2
=21-73*2+6*21
=7*21-73*2
得 21 -1≡7(mod73).
例:求7的模96逆
做辗转相除法, 求得整数b,k使得 7b+96k=1, 则b是7的模96逆.
计算如下:
96=7*13+5
7=5*1+2
5=2*2+1
回代 1=5-2*2
1=5-(7-5*1)*2
=5*3-7*2
=(96-7*13)*3-7*2
=96*3-41*7
-41 mod 96 =55 所以55就是7关于96的逆元。
得 7 -1≡55(mod96).
C#中实现如下:
 View Code
View Code
public static int GetOpposite(int num, int modeNum)
{
int opposite = 0;
int remainder = 0;
int temp1 = 0;
int temp2 = 1;
//将较小的数作为 modeNum
if (modeNum > num)
{
num = num + modeNum;
modeNum = num - modeNum;
num = num - modeNum;
}
//将num 保存起来,如果最终的余数小于零,将其转换成大于零的数
int tempNum = num;
do
{
remainder = num % modeNum;
if (remainder!= 0)
{
opposite = -1 * num / modeNum * temp2 + temp1;
}
temp1 = temp2;
temp2 = opposite;
num = modeNum;
modeNum = remainder;
}
while (remainder!= 0);
return opposite>0?opposite:opposite+tempNum;
}
//求两个数的最大公约数
public static int Gcd(int a, int b)
{
int temp;
if (b > a)
{
temp = a;
a = b;
b = temp;
}
while (b != 0)
{
temp = a % b;
a = b;
b = temp;
}
return a;
}
测试程序如下:
int num, modeNum;
while (true)
{
num = Int32.Parse(Console.ReadLine());
modeNum = Int32.Parse(Console.ReadLine());
int gcd=Gcd(num, modeNum);
//不互为质数,有公约数
if (gcd!= 1)
{
Console.Write("有公约数,公约数为:" + gcd.ToString() + "\n");
Console.ReadKey();
continue;
}
int opposite = GetOpposite(num, modeNum);
Console.Write("opposite=" + opposite.ToString() + "\n");
Console.ReadKey();
}