软工实践第二次作业——数独

GIT传送门

估计耗费时间：

---

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	60
· Estimate	· 估计这个任务需要多少时间	60
Development	开发	710
· Analysis	· 需求分析 (包括学习新技术)	240
· Design Spec	· 生成设计文档	50
· Design Review	· 设计复审 (和同事审核设计文档)	40
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	40
· Design	· 具体设计	60
· Coding	· 具体编码	180
· Code Review	· 代码复审	50
· Test	· 测试（自我测试，修改代码，提交修改）	50
Reporting	报告	200
· Test Report	· 测试报告	120
· Size Measurement	· 计算工作量	40
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	40
合计		970

解题思路描述：

---

• 查找了部分资料，总结了下行列变换法的关键就是要找到中心小九宫跟这整个数独存在的某种特殊行列坐标的上的联系。在设计实现过程中给出了流程图。

  

• 这是基本的构造公式，由中心的九宫出发，进行上下左右的移位运算，得到了上图的构造公式。当然，再随机定义任意两行进行简单几次的行列交换，就很容易得到百万数量级的数独。当然要是测试数据真的有千万级别的还请手下留情。

设计实现过程：

---

• 代码关键元素：

  • arrFa数组；
  • traceSudo()函数；
  • printSudo()函数；

• arrFa = {1,2,3,4,5,6,7,8,9}是构建数独的基础数据，规定了1-9个数据。traceSudo()函数用于构建初始中心九宫，并且完成从中心九宫到数独的演变。printSudo()函数是用于输出。这里参考了同学的意见，putchar的输出效率比printf来的高。

• 最后用一个do while包围，实现一个对arrFa的全排列

代码说明：

---

• 输出函数

void printSudo(int arr[E][E], int i, int j) {
	for (int k = 0; k < i; k++) {
		for (int m = 0; m < j; m++) {
			putchar(arr[k][m] + 48);
			putchar(' ');
		}
		putchar('\n');
	}
	putchar('\n');
}

• 生成函数（其实有部分可以合并，但便于以后自己的阅读理解还是决定分步书写）

void traceSudo(int n, int count) {
	int sudoarr[9][9] = { 0 };
	int arrFaIndex = 0;
	//生成中间元数组 
	int arrPart[3][3];
	int loop = 1; //三重全排列退出条件
				  //用到了三重全排列对4-6,7-9行进行完全排列 
	do {
		arrFaIndex = 0;
		for (int i = 2; i >= 0; i--) {
			for (int j = 2; j >= 0; j--) {
				arrPart[i][j] = (arrFa[arrFaIndex] + 3) % 9 + 1;    //由于要求第一数字固定，我的学号是（0 + 4）% 9 + 1 = 5
				arrFaIndex++;
			}
		}
		int k = 0, m = 0;
		/*
		* 构建数独中部
		*/
		for (int i = 3; i<6; i++) {
			for (int j = 3; j<6; j++) {
				sudoarr[i][j] = arrPart[k][m];
				m++;
			}
			m = 0;
			k++;
		}
		/*
		* 构建数独左部
		*/
		for (int i = 3; i<6; i++) {
			for (int j = 0; j<3; j++) {
				sudoarr[i][j] = arrPart[(i + 2) % 3][j];
			}
		}
		/*
		* 构建数独右部
		*/
		for (int i = 3; i<6; i++) {
			for (int j = 6; j<9; j++) {
				sudoarr[i][j] = arrPart[(i - 2) % 3][j - 6];
			}
		}
		/*
		* 构件数独上部
		*/
		for (int i = 0; i<3; i++) {
			for (int j = 3; j<6; j++) {
				sudoarr[i][j] = arrPart[i][(j + 2) % 3];
			}
		}
		/*
		* 构建数独下部
		*/
		for (int i = 6; i<9; i++) {
			for (int j = 3; j<6; j++) {
				sudoarr[i][j] = arrPart[i - 6][(j - 2) % 3];
			}
		}
		/*
		* 构建数独左上部
		*/
		for (int i = 0; i<3; i++) {
			for (int j = 0; j<3; j++) {
				sudoarr[i][j] = arrPart[(i + 2) % 3][(j + 2) % 3];
			}
		}
		/***********************/


		/*
		* 构建数独右上部
		*/
		m = 0; k = 0;
		for (int i = 0; i<3; i++) {
			for (int j = 0; j<3; j++) {
				arrPart[k][m] = sudoarr[i][j];
				m++;
			}
			m = 0; k++;
		}
		for (int i = 0; i<3; i++) {
			for (int j = 6; j<9; j++) {
				sudoarr[i][j] = arrPart[(i + 2) % 3][j - 6];
			}
		}
		/*
		* 构建数独左下部
		*/
		m = 0; k = 0;
		for (int i = 6; i<9; i++) {
			for (int j = 3; j<6; j++) {
				arrPart[k][m] = sudoarr[i][j];
				m++;
			}
			m = 0; k++;
		}
		for (int i = 6; i<9; i++) {
			for (int j = 0; j<3; j++) {
				sudoarr[i][j] = arrPart[(i + 2) % 3][j];
			}
		}
		/*
		* 构建右下部
		*/
		for (int i = 6; i<9; i++) {
			for (int j = 6; j<9; j++) {
				sudoarr[i][j] = arrPart[(i - 2) % 3][j - 6];
			}
		}
		for (int i = 3; i < 9; i++) {
			for (int j = 0; j < 9; j++) {
				temp[i][j] = sudoarr[i][j];
			}
		}

		do {
			for (int i = 0; i < 9; i++) {
				sudoarr[3][i] = temp[a46[0]][i];
				sudoarr[4][i] = temp[a46[1]][i];
				sudoarr[5][i] = temp[a46[2]][i];
			}
		
			do {
				for (int i = 0; i < 9; i++) {
					sudoarr[6][i] = temp[a79[0]][i];
					sudoarr[7][i] = temp[a79[1]][i];
					sudoarr[8][i] = temp[a79[2]][i];
				}
				printSudo(sudoarr, 9, 9);
				count++;
				if (count == n) {
					loop = 0;
				}
			} while (next_permutation(a79, a79 + 3) && loop == 1);
		} while (next_permutation(a46, a46 + 3) && loop == 1);
	} while (next_permutation(arrFa, arrFa + 9) && loop == 1);

}

测试运行：

---

• 能够在输入错误的时候给出Error的提示

性能分析：

---

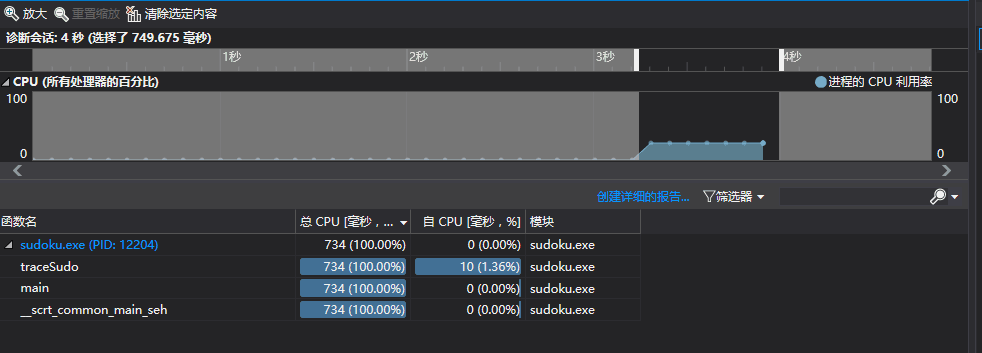
• n = 100000，由图可知十万级数据几乎秒算

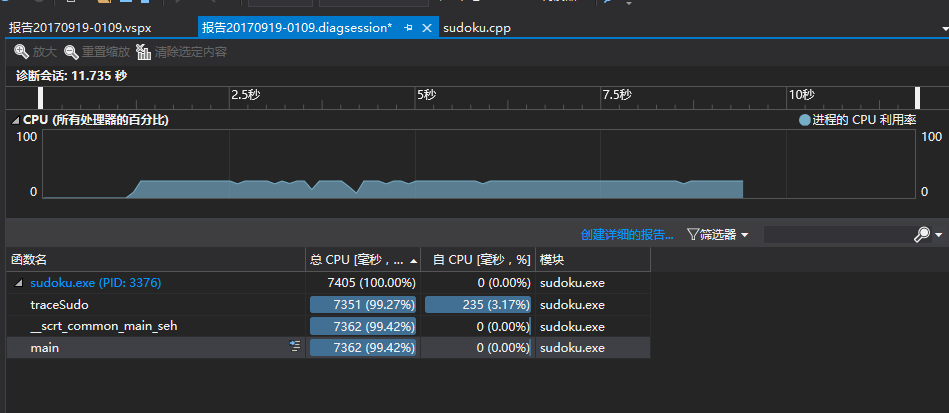
• n = 1000000，由下面两张图可知百万级数据耗时大概7-8秒

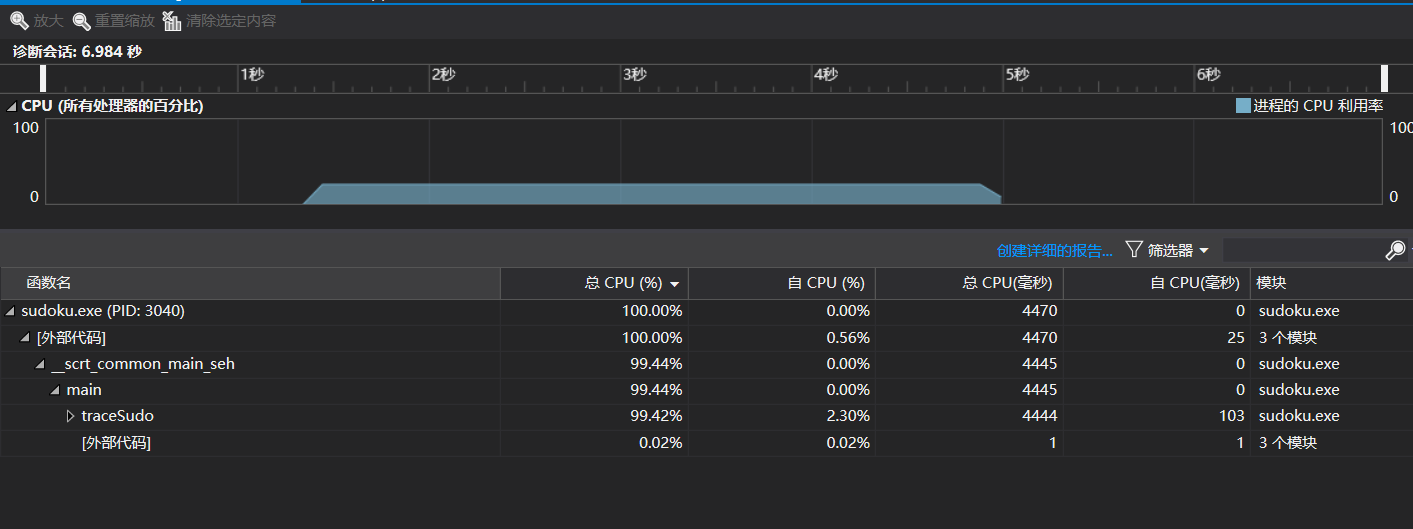
• n = 1000000，如果是调用printf则需要耗时28-32秒。更变态的是如果你用的cout的话，那就真的是僵硬了。

• 因此printSudo()函数的效率关系到整个程序的效率。在整个代码中，我们优先考虑的不是精简算法本身，而是要从输出入手，可以节约近1分40秒（Release X64）。

• 新增：由于老师要求改变，我发现用到了三重全排列的时候，效率提高了近百分五十，总体在4-5秒（n = 1000000）。
  

总结：

• 其实对我来说，这次作业真的很赶，一整个周末除了看了场电影几乎全砸在了软工实践上。Git的使用掌握了很久，感谢同学的帮助，对Markdown排版也略知一二了。我一直想尽最快速度完成，也询问了助教，不过她好像并不怎么着急233，早知道也不用那么赶啦。

• 解题关键这里也不赘述了，上面写的很清楚。C支持了一个全排列函数，其实这个函数算是误打误撞知道的。之前学java的想搜它的全排列函数，结果找到了C语言的。

• 大多数人都意识到了，其实输出所占用的时间，远比算法本身来的夸张，因此都会往如何减少读写文件时间上考虑，我也是如此。在数据结构的练习中，我们知道printf比cout在兼容体制下高效得多。输出到文件用putchar甚至能给你带来意外的惊喜，这里还是感谢同学在我一筹莫展时给予的点子。

• PSP

---

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	60	60
· Estimate	· 估计这个任务需要多少时间	60	60
Development	开发	710	740
· Analysis	· 需求分析 (包括学习新技术)	240	250
· Design Spec	· 生成设计文档	50	60
· Design Review	· 设计复审 (和同事审核设计文档)	40	40
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	40	40
· Design	· 具体设计	60	80
· Coding	· 具体编码	180	160
· Code Review	· 代码复审	50	50
· Test	· 测试（自我测试，修改代码，提交修改）	50	60
Reporting	报告	200	200
· Test Report	· 测试报告	120	110
· Size Measurement	· 计算工作量	40	50
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	40	40
合计		970	1000