从局部坐标系到世界坐标系, 向量解奥秘

基底

以X,Y轴为基底

在平面直角坐标系中，我们分别取与X轴、Y轴正方向相同的两个单位向量 i，j 作为一组基底

根据向量加法与数乘运算法则, 其它任意向量可以表示为 a = xi + yj, 简记为 (x, y), 平面直角坐标系中的点转变成了相对于原点的向量.

以X1,Y1轴为基底(X1与Y1互相垂直, 两轴交点为原点, X1轴相对于X轴旋转了θ)

在这里，我们分别取与X1轴、Y1轴正方向相同的两个单位向量 i1，j1 作为一组基底

i1以 X-Y 为基底可以表示为 (cosθ, sinθ)

j1以 X-Y 为基底可以表示为 (-sinθ, cosθ)

根据向量加法与数乘运算法则, 其它任意向量可以表示为 a = x1i1 + y1j1, 平面直角坐标系中的点又转变成了X1-Y1新坐标系统中相对于原点的向量.

向量本身并没有发生变化

所以有 (x, y) = x1i1 + y1j1

　　　　　　  = (x1.cosθ, x1.sinθ) + (-y1.sinθ, y1.cosθ)

　　　　　　  = (x1.cosθ -y1.sinθ, x1.sinθ + y1.cosθ)

用向量与矩阵表示为:

(x, y) = (x1, y1)  X [cosθ, sinθ]

　　　　　　　　　   [-sinθ, cosθ]

结论:

　　如果把 i1,j1 组成的基底叫局部坐标系, i,j组成的基底叫世界坐标系, 上面的式子不就是从局部坐标系到世界坐标系的旋转变换吗?

 

二维逆矩阵:

　　

 

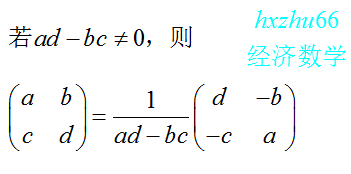
大道至简! 万物有缘, 殊途同归!