对缓存的思考【续】——编写高速缓存友好代码
开篇
上一篇博文对缓存的思考——提高命中率详细介绍了高速缓存的组织结构，并通过实例说详细明了cpu从高速缓存中取数据的过程，对于缓存的工作机制应该有了清晰的认识。这篇博文就来简单讨论以下对于缓存在实际开发中的应用，这里将告诉你如何让你的程序充分利用该缓存，即如何编写高速缓存友好的代码。
提示：如果高速缓存的运行机制还没有清晰的认识，请参照前面文章。
注1：关于文中提到的局部性的相关知识参照：局部性原理浅析——良好代码的基本素质
注2：这是一个系列的文章，收录在 程序性能优化
注3：文章知识有些地方不容易理解，所以用心才能看完噢。
“用空间换时间”
在搞算法的时候经常能听到这种说法，算法研究中通常要考虑算法的时间、空间复杂度。而这里“用空间换时间”说的是通过牺牲一些存储块代码更有效的利用缓存。从而提高程序的运行效率。可见，高效的代码不仅依赖于良好的算法，编写缓存有好代码也很重要。
我们将通过下面的例子来认识这一过程
注：这里假设高速缓存是直接映射的，即每一组只有一行。
通过”局部性“相关的知识，我们可以看出上面的代码有良好的空间局部性：一维向量 x[ ] 、y[ ] 都是对其元素进行步长为1的顺序访问。那么，拥有良好局部性的代码，是否就能有效的利用高速缓存呢。不一定。
设上面代码运行在拥有直接映射缓存的计算机上。
为了把问题描述清楚，这里有一些假设
1、float 是4 byte，所以数组x[ ]占用空间为32byte，y[ ]也一样
2、x[ ]存储在内存中地址0-31的位置，y[ ]紧随其后在地址开始为32的连续位置。（如果觉得牵强你可理解为虚拟地址）
3、直接映射高速缓存有两个组，每组的大小为16byte。也就是高速缓存中每组可存储4个元素。
根据这些假设，每个x[i]、y[i]会被映射到相同的高速缓存组
元素和缓存之间的映射关系如下图所示
图被中间的双线条分为左右两栏，左边是x[ ]的情况，右边y[ ]的情况。
看左边的一栏，左边的一列代表的x 中的元素，中间的是元素在内存中的地址，第三列是该元素映射在缓存中的组号。
为什么会是这样分配的呢，其实在上一篇博文中就有提到。（参看前面的博客会有更好的效果）
这里还是简单的说一下：
主存中的数据是根据地址被映射到缓存的不同位置的，二进制地址的不同位代表不同的信息，一般来说从左到右分别代表：行、组、偏移。
缓存的每一行是16byte，从而可推断缓存的地址位是4 。因为4个二进制的组合共有16种情况（也即2的4次方是16）。
下表是它们地址各个位及代表的信息。
X[ ]:
注：这里的地址不是元素的真实地址，指的是块地址。x有八个元素，每个元素占四个byte，我们把这四个byte当作一个整体， 那么x[0]就是第一块，x[1]为第二块，以此类推。y的情况相同。
上图中，阴影部分的为地址的二进制表示形式。每个地址被表示成了四位的二进制数。
其中：
左边一位标记行。因为是直接映射，每组只有一行，所以一位就能表示。
左边第二位标记组。我们讨论的这个缓存只有两个组，一位就能标记。
右边两表示偏移。每行中有四个数据块，所以两位能标识。
可以看出，x[ ]的前四个元素属于同一组，后四个为另一组。
下面是y[]的情况：
现在对于刚才那个图（如下）应该有更清楚的认识了把。
x[i]和y[i]有相同的组标记、不同的行标记，这就意味着x[i]和y[i]不能同时存在于缓存中。
下面模拟一下上述代码的执行过程。我们假设局部变量sum存于cpu寄存器中。
计算x[0]*y[0]
取x[0]
刚开始的时候缓存还没预热，每一行的标记为都为不可用。所以取x[0]的时候缓存不命中，缓存从下一级存储中取出包括x[0]的整行，放入缓存第0组中，并返回x[0]给cpu。这时缓存第一组中的元素有x[0]、x[1]、x[2]、x[3]
此时缓存的情况如下图所示
缓存中的元素为蓝色背景的部分
组序号为1的行都还没初始化。
取y[0]
y[0]对应的块地址是8，即1 0 00 组标记是0，行标记1，不命中。于是取出包括y[0]的行，并放入缓存中。此时的缓存情况：
取x[1]，缓存不命中，当取了x[0]本有x[1]在缓存中，当取y[0]的时候，这一行被覆盖了。所以只能把包括x[1]行的行取出放入缓存（覆盖y行），并返回x[1]。取了x[1]后的缓存情况和取出x[0]的情况一样：
当取y[1]的时候，缓存不命中，又把上面x行替换为y行。
可以推理出，取出x和y 的元素总是不命中。
空间换时间
因为x[i]、y[i]映射到了相同的组，现在的这种情况称为冲突不命中，每次对x和y 的引用都会造成冲突不命中。这一情况用“抖动”来描述。
简单的说，即使程序有良好的时间局部性，且缓存也有足够大小的空间来缓存，也会发生抖动。因为x[i]、y[i]被映射到了相同的缓存组。
幸运的是，可以修正这种情况，让x[i],y[i]映射到不同的缓存组。
一个简单的方法就是增加x的长度。给x分配12个float大小的空间。这样y的其实地址就是18而不是32
如下图所示：
这样当引用x[0]的时候把x[0]、x[1]、x[2]、x[3]放入组0中，引用y[0]的时候把y[0],y[1],y[2],y[3]放入组1 中。
于是对引用x[1]~x[3]的引用就就能直接从缓存中获取，同样对y[1]~y[3]的引用也能从缓存中获取
相比于刚开始的情况，大大增加了缓存的使利用。同时也提高了程序的性能，特别是当数据量很大的时候。
实质通过在x的后面追加元素，让y的其实地址后移，让y对应的组号发生改变。当然在x后面追加元素只是占用了一部分空间，那些空间并没有被利用，但是提高了程序的性能。
所以才说“用空间换时间”
为什么用中间位作为组索引?
用中间位作为组索引是有原因的。
如果用最高位做索引
情况如上图中的中间所示，连续的块都别映射到了同一个组中（特别的，如果是直接映射高速缓存，连续的块被映射到同一行中）这样的确也能利用缓存，如上图所示，当引用第一个元素的时候，会把第1、2、3、4个拷贝到缓存的组0中，以后对2、3、4的引用就能直接在缓存中提取。引用第5个元素的时候，把第5、6、7、8个拷贝到缓存的组1中，同样的，对4、5、6的引用能直接在缓存中提取。后面的情况类似就不再叙述。
通过上面的叙述，你可能已经发现一个问题：当对缓存的组1进行操作的时候，缓存中的其它组是没有被利用的，这和缓存中只有一个组其实效果是一样的。对缓存中的其他组没有很好的利用，也就是说，虽然也有缓存的利用，但有最大化。
改用中间位做索引，如上图中的右图所示，同一组中的块不再是连续的，这样可以保证缓存中的所有组都能被有效的利用。
引用第1个元素的时候，将把第1、5、9、13放入缓存组1中
引用第2个元素的时候， 把第2、6、10、14放入缓存
引用第3个，把3、7、11、15放入缓存
引用第4个，把4、8、12、16放入缓存
这样对前四个元素的引用都不会命中，而而对后面的引用都能命中。这种过程也就是所谓的缓存预热。
高速缓存友好代码
一维数组
上面的讨论我们假设了一种特殊的情况，下面将对如何编写高速缓存友好代码做更加泛化的讨论
先看下面的代码
很容易看出，上面的代码有良好的局部性。编译器对代码优化的时候 ，通常会将局部变量用寄存器保存（因为他们在函数结束时就会被释放）。一般来说，如果一个高速缓存块大小为Bbyte，那么在一个步长为k的引中，平均每次迭代会有min (1; (wordsize k)=B )次缓存不命中。k=1时取最小值。
Example
假设v是块对齐的，字为4个字节，高速缓存块为4个字，高速缓存初始化为空。那么对v的步长为1 的引用情况如下所示
图中的m，表示miss，即不命中；h表示hit 表示命中。
这个例子中，对v[0]的引用不命中，而接下来对v[2]~v[4]的引用命中，
对v[5]不命中，接下来对v[6]~v[7]引用命中。
上面的叙述说明了两个问题:
1、对局部变量的反复引用是好的，因为他们存在寄存器中，访问数度很快
2、对步长为1的引用是好的，因为存储器结构中将数据存放为连续的块
多维数组
在对多维数组的操作中，空间局部性尤为重要。
考虑下面的例子
c语言以行序为主序的，所以上述代码刚好是对数组a[][]的步长为1的引用，和上一种情况一样，假设刚开始的缓存是冷缓存（刚开始的时候缓存里没有任何数据）。那么对数组a[][]的访问将得到如下图所示的命中和不命中模式：
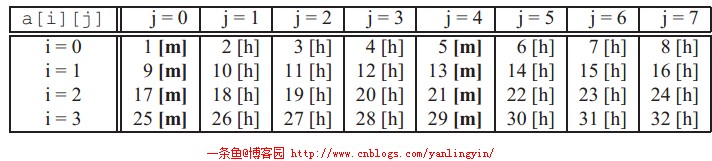
对缓存有良好的使用。
然而，对代码做一个微小的改动之后：
这时以步长4对数组a[][]的元素进行引用，这种情况对数组将是一列一列引用而不是一行一行引用的。他们在缓存中的命中情况如下所示
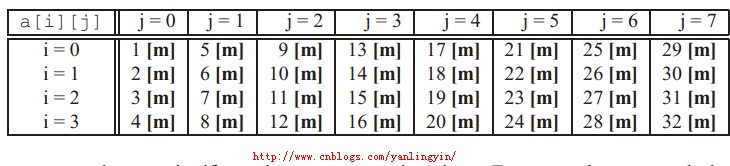
较高的不命中率对程序的运行效率有显著影响，因为从第一层存储中取出数据将花费比缓存中取数据多很多的时钟周期。
小结
好的程序代码不仅要有好的算法，对计算机硬件的充分利用也是很关键的一步， 前面几篇文章主要只是从缓存角度做了分析。
在缓存角度，要提高程序运行效率，编写缓存友好代码尤为关键，这也是区分程序员层次的一个标准，要求较高，需要你掌握缓存的工作原理，缓存内部的组织形式，还需要编译相关的知识，前面还有很多知识等值我们去学习，这里只是总结了自己的学习成果，分享给大家，希望对各位园友有用。
我觉得写博客不是我的目的，博客只是我学习过程中的副产品而已，对于某些知识，你知道它是一回事，要把它讲出来却非得把它弄透彻不可，我把写博客当作学习的一部分，在总结的过程中提高，还能把成果分享，我想这就是博客最大的价值把，我们都应该享受写博客的这个过程。
预：下一篇博文中会从缓存角度对《编程之美》中的一道题目做个讨论，里面的算法很巧妙，表面上看性能是提高了，从缓存角度却不然。
全文完。
参看资料：computer systems
如有转载请注明出处：http://www.cnblogs.com/yanlingyin/
一条鱼、尹雁铃@ 博客园 2012-2-12
E-mail：yanlingyin@yeah.net
