[Unity] A-Star(A星)寻路算法
在游戏中,有一个很常见地需求,就是要让一个角色从A点走向B点,我们期望是让角色走最少的路。嗯,大家可能会说,直线就是最短的。没错,但大多数时候,A到B中间都会出现一些角色无法穿越的东西,比如墙、坑等障碍物。这个时候怎么办呢? 是的,我们需要有一个算法来解决这个问题,算法的目标就是计算出两点之间的最短路径,而且要能避开障碍物。
百度百科:
A*搜寻算法俗称A星算法。这是一种在图形平面上,有多个节点的路径,求出最低通过成本的算法。常用于游戏中的NPC的移动计算,或线上游戏的BOT的移动计算上。
简化搜索区域
要实现寻路,第一步我们要把场景简化出一个易于控制的搜索区域。
怎么处理要根据游戏来决定了。例如,我们可以将搜索区域划分成像素点,但是这样的划分粒度对于一般的游戏来说太高了(没必要)。
作为代替,我们使用格子(一个正方形)作为寻路算法的单元。其他的形状类型也是可能的(比如三角形或者六边形),但是正方形是最简单并且最常用的。
比如地图的长是w=2000像索,宽是h=2000像索,那么我们这个搜索区域可以是二维数组 map[w, h], 包含有400000个正方形,这实在太多了,而且很多时候地图还会更大。
现在让我们基于目前的区域,把区域划分成多个格子来代表搜索空间(在这个简单的例子中,20*20个格子 = 400 个格子, 每个格式代表了100像索):

既然我们创建了一个简单的搜索区域,我们来讨论下A星算法的工作原理吧。
我们需要两个列表 (Open和Closed列表):
- 一个记录下所有被考虑来寻找最短路径的格子(称为open 列表)
- 一个记录下不会再被考虑的格子(成为closed列表)
首先在closed列表中添加当前位置(我们把这个开始点称为点 “A”)。然后,把所有与它当前位置相邻的可通行格子添加到open列表中。
现在我们要从A出发到B点。
在寻路过程中,角色总是不停从一个格子移动到另一个相邻的格子,如果单纯从距离上讲,移动到与自身斜对角的格子走的距离要长一些,而移动到与自身水平或垂直方面平行的格子,则要近一些。
为了描述这种区别,先引入二个概念:
节点(Node):每个格子都可以称为节点。
代价(Cost):描述角色移动到某个节点时所走的距离(或难易程度)。
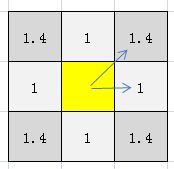
如上图,如果每水平或垂直方向移动相邻一个节点所花的代价记为1,则相邻对角节点的代码为1.4(即2的平方根--勾股定理)
通常寻路过程中的代价用f,g,h来表示
g代表(从指定节点到相邻)节点本身的代价--即上图中的1或1.4
h代表从指定节点到目标节点(根据不同的估价公式--后面会解释估价公式)估算出来的代价。
而 f = g + h 表示节点的总代价
/// <summary> /// 寻路节点 /// </summary> public class NodeItem { // 是否是障碍物 public bool isWall; // 位置 public Vector3 pos; // 格子坐标 public int x, y; // 与起点的长度 public int gCost; // 与目标点的长度 public int hCost; // 总的路径长度 public int fCost { get {return gCost + hCost; } } // 父节点 public NodeItem parent; public NodeItem(bool isWall, Vector3 pos, int x, int y) { this.isWall = isWall; this.pos = pos; this.x = x; this.y = y; } }
注意:这里有二个新的东东 isWall 和 parent。
通常障碍物本身也可以看成是由若干个不可通过的节点所组成,所以 isWall 是用来标记该节点是否为障碍物(节点)。
另外:在考查从一个节点移动到另一个节点时,总是拿自身节点周围的8个相邻节点来说事儿,相对于周边的节点来讲,自身节点称为它们的父节点(parent).
前面一直在提“网格,网格”,干脆把它也封装成类Grid.cs
using UnityEngine; using System.Collections; using System.Collections.Generic; public class Grid : MonoBehaviour { public GameObject NodeWall; public GameObject Node; // 节点半径 public float NodeRadius = 0.5f; // 过滤墙体所在的层 public LayerMask WhatLayer; // 玩家 public Transform player; // 目标 public Transform destPos; /// <summary> /// 寻路节点 /// </summary> public class NodeItem { // 是否是障碍物 public bool isWall; // 位置 public Vector3 pos; // 格子坐标 public int x, y; // 与起点的长度 public int gCost; // 与目标点的长度 public int hCost; // 总的路径长度 public int fCost { get {return gCost + hCost; } } // 父节点 public NodeItem parent; public NodeItem(bool isWall, Vector3 pos, int x, int y) { this.isWall = isWall; this.pos = pos; this.x = x; this.y = y; } } private NodeItem[,] grid; private int w, h; private GameObject WallRange, PathRange; private List<GameObject> pathObj = new List<GameObject> (); void Awake() { // 初始化格子 w = Mathf.RoundToInt(transform.localScale.x * 2); h = Mathf.RoundToInt(transform.localScale.y * 2); grid = new NodeItem[w, h]; WallRange = new GameObject ("WallRange"); PathRange = new GameObject ("PathRange"); // 将墙的信息写入格子中 for (int x = 0; x < w; x++) { for (int y = 0; y < h; y++) { Vector3 pos = new Vector3 (x*0.5f, y*0.5f, -0.25f); // 通过节点中心发射圆形射线,检测当前位置是否可以行走 bool isWall = Physics.CheckSphere (pos, NodeRadius, WhatLayer); // 构建一个节点 grid[x, y] = new NodeItem (isWall, pos, x, y); // 如果是墙体,则画出不可行走的区域 if (isWall) { GameObject obj = GameObject.Instantiate (NodeWall, pos, Quaternion.identity) as GameObject; obj.transform.SetParent (WallRange.transform); } } } } // 根据坐标获得一个节点 public NodeItem getItem(Vector3 position) { int x = Mathf.RoundToInt (position.x) * 2; int y = Mathf.RoundToInt (position.y) * 2; x = Mathf.Clamp (x, 0, w - 1); y = Mathf.Clamp (y, 0, h - 1); return grid [x, y]; } // 取得周围的节点 public List<NodeItem> getNeibourhood(NodeItem node) { List<NodeItem> list = new List<NodeItem> (); for (int i = -1; i <= 1; i++) { for (int j = -1; j <= 1; j++) { // 如果是自己,则跳过 if (i == 0 && j == 0) continue; int x = node.x + i; int y = node.y + j; // 判断是否越界,如果没有,加到列表中 if (x < w && x >= 0 && y < h && y >= 0) list.Add (grid [x, y]); } } return list; } // 更新路径 public void updatePath(List<NodeItem> lines) { int curListSize = pathObj.Count; for (int i = 0, max = lines.Count; i < max; i++) { if (i < curListSize) { pathObj [i].transform.position = lines [i].pos; pathObj [i].SetActive (true); } else { GameObject obj = GameObject.Instantiate (Node, lines [i].pos, Quaternion.identity) as GameObject; obj.transform.SetParent (PathRange.transform); pathObj.Add (obj); } } for (int i = lines.Count; i < curListSize; i++) { pathObj [i].SetActive (false); } } }
在寻路的过程中“条条道路通罗马”,路径通常不止一条,只不过所花的代价不同而已。
所以我们要做的事情,就是要尽最大努力找一条代价最小的路径。
但是,即使是代价相同的最佳路径,也有可能出现不同的走法。
用代码如何估算起点与终点之间的代价呢?
//曼哈顿估价法 private function manhattan(node:Node):Number { return Math.abs(node.x - _endNode.x) * _straightCost + Math.abs(node.y + _endNode.y) * _straightCost; } //几何估价法 private function euclidian(node:Node):Number { var dx:Number=node.x - _endNode.x; var dy:Number=node.y - _endNode.y; return Math.sqrt(dx * dx + dy * dy) * _straightCost; } //对角线估价法 private function diagonal(node:Node):Number { var dx:Number=Math.abs(node.x - _endNode.x); var dy:Number=Math.abs(node.y - _endNode.y); var diag:Number=Math.min(dx, dy); var straight:Number=dx + dy; return _diagCost * diag + _straightCost * (straight - 2 * diag); }
上面的代码给出了三种基本的估价算法(也称估价公式),其算法示意图如下:
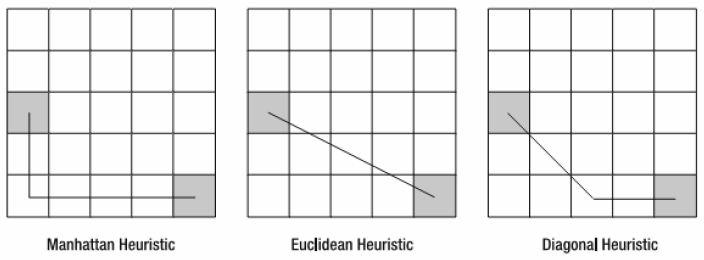
如上图,对于“曼哈顿算法”最贴切的描述莫过于孙燕姿唱过的那首成名曲“直来直往”,笔直的走,然后转个弯,再笔直的继续。
“几何算法”的最好解释就是“勾股定理”,算出起点与终点之间的直线距离,然后乘上代价因子。
“对角算法”综合了以上二种算法,先按对角线走,一直走到与终点水平或垂直平行后,再笔直的走。
这三种算法可以实现不同的寻路结果,我们这个例子用的是“对角算法”:
// 获取两个节点之间的距离 int getDistanceNodes(Grid.NodeItem a, Grid.NodeItem b) { int cntX = Mathf.Abs (a.x - b.x); int cntY = Mathf.Abs (a.y - b.y); // 判断到底是那个轴相差的距离更远 , 实际上,为了简化计算,我们将代价*10变成了整数。 if (cntX > cntY) { return 14 * cntY + 10 * (cntX - cntY); } else { return 14 * cntX + 10 * (cntY - cntX); } }
好吧,下面直接贴出全部的寻路算法 FindPath.cs:
using UnityEngine; using System.Collections; using System.Collections.Generic; public class FindPath : MonoBehaviour { private Grid grid; // Use this for initialization void Start () { grid = GetComponent<Grid> (); } // Update is called once per frame void Update () { FindingPath (grid.player.position, grid.destPos.position); } // A*寻路 void FindingPath(Vector3 s, Vector3 e) { Grid.NodeItem startNode = grid.getItem (s); Grid.NodeItem endNode = grid.getItem (e); List<Grid.NodeItem> openSet = new List<Grid.NodeItem> (); HashSet<Grid.NodeItem> closeSet = new HashSet<Grid.NodeItem> (); openSet.Add (startNode); while (openSet.Count > 0) { Grid.NodeItem curNode = openSet [0]; for (int i = 0, max = openSet.Count; i < max; i++) { if (openSet [i].fCost <= curNode.fCost && openSet [i].hCost < curNode.hCost) { curNode = openSet [i]; } } openSet.Remove (curNode); closeSet.Add (curNode); // 找到的目标节点 if (curNode == endNode) { generatePath (startNode, endNode); return; } // 判断周围节点,选择一个最优的节点 foreach (var item in grid.getNeibourhood(curNode)) { // 如果是墙或者已经在关闭列表中 if (item.isWall || closeSet.Contains (item)) continue; // 计算当前相领节点现开始节点距离 int newCost = curNode.gCost + getDistanceNodes (curNode, item); // 如果距离更小,或者原来不在开始列表中 if (newCost < item.gCost || !openSet.Contains (item)) { // 更新与开始节点的距离 item.gCost = newCost; // 更新与终点的距离 item.hCost = getDistanceNodes (item, endNode); // 更新父节点为当前选定的节点 item.parent = curNode; // 如果节点是新加入的,将它加入打开列表中 if (!openSet.Contains (item)) { openSet.Add (item); } } } } generatePath (startNode, null); } // 生成路径 void generatePath(Grid.NodeItem startNode, Grid.NodeItem endNode) { List<Grid.NodeItem> path = new List<Grid.NodeItem>(); if (endNode != null) { Grid.NodeItem temp = endNode; while (temp != startNode) { path.Add (temp); temp = temp.parent; } // 反转路径 path.Reverse (); } // 更新路径 grid.updatePath(path); } // 获取两个节点之间的距离 int getDistanceNodes(Grid.NodeItem a, Grid.NodeItem b) { int cntX = Mathf.Abs (a.x - b.x); int cntY = Mathf.Abs (a.y - b.y); // 判断到底是那个轴相差的距离更远 if (cntX > cntY) { return 14 * cntY + 10 * (cntX - cntY); } else { return 14 * cntX + 10 * (cntY - cntX); } } }
运行效果图:
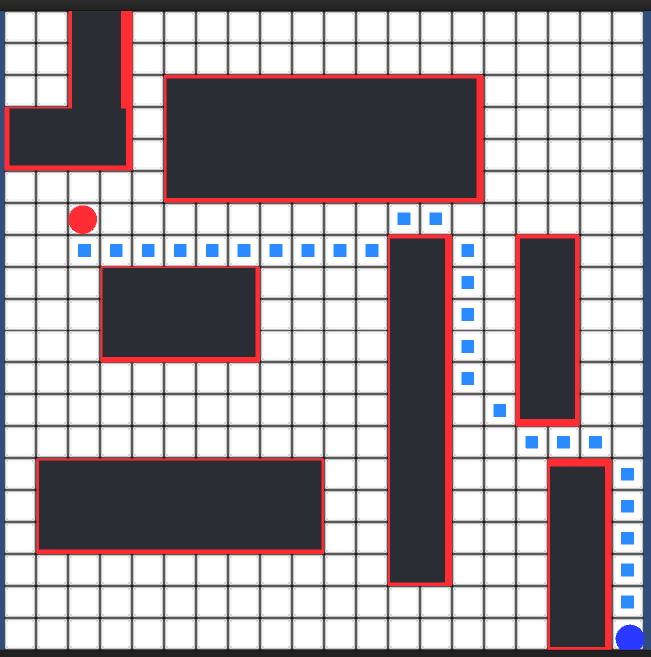
红色区域是标识出来的不可以行走区域。(代码中对两个点的定位有点小小的问题,不过不影响算法的演示,我也就懒得改了)
完整代码下载:
http://pan.baidu.com/s/1jInjLDs
转载注明出处。


