A*算法改进——Any-Angle Path Planning的Theta*算法与Lazy Theta*算法
本文是该篇文章的归纳http://aigamedev.com/open/tutorial/lazy-theta-star/#Nash:07 。
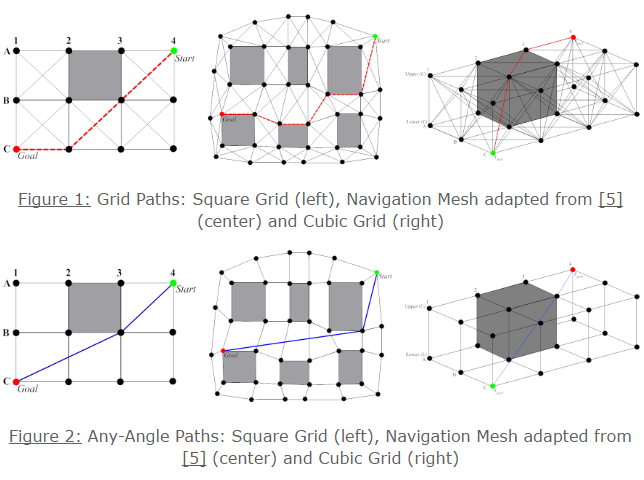
传统的A*算法中,寻找出来的路径只能是沿着给出的模型(比如TileMap、网格模型)上的路径依次行走。(上图上半)
在游戏中寻路的场合下,这种路径看起来是十分不自然的。与之相对的“自然的”寻路称为Any-Angle Path Planning。(上图下半)
对于A*的一个简单的修正是,在生成路径之后,检测路径上隔开的两个点之间是否有line of sight(即视线,以下简称LOS),有的话便可以把中间的点删除,让人物直接穿过。这种方法称之为A* with post-smoothed paths。依据如何选取这两个点,最终优化的效果不同。但是要注意的是这种修正得到的路径的质量和效率是需要取舍的。
另外,本文介绍的算法都不保证寻找的路径是最佳的。不要尝试用来刷题233。
Theta*
修正的第二种办法,即Theta*算法。这种算法是A*的一种改进,关键在于其打开一个节点s,然后更新周围的节点s'时,会检查s'与parent(s)的可见性。如果可见,则把s'的父节点设置成parent(s)。

左边是\A*算法,中间是Theta*算法,右边是等下介绍的Lazy Theta*。
可以看到在Theta*中,除了ComputeCost函数之外,其他的内容和A*算法是相同的。
在ComputeCost中,A*算法计算一个点s'的新的g,如果比原来的更好,则将原来的parent和g换成新的。
在Theta*中,则在计算前,先去计算s'和s的parent有无视线。如果有视线,则把s'的parent和g以s的parent为parent进行更新。否则跟A*一样处理。
然而,Theta*有一个很大的问题,就是需要做大量的line of sight检查。有多少个点进入过open列表,就有多少次检查。在较为细致的网格中这个数量是十分巨大的。
Lazy Theta*
这里就引出了Theta*的一种优化,即Lazy Theta*。
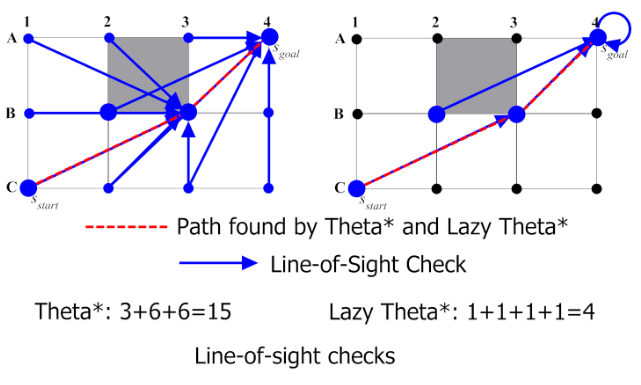
两种算法进行的LOS检查数。
Lazy Theta*的核心思想在于,将line of sight检查延迟到打开该节点为止。
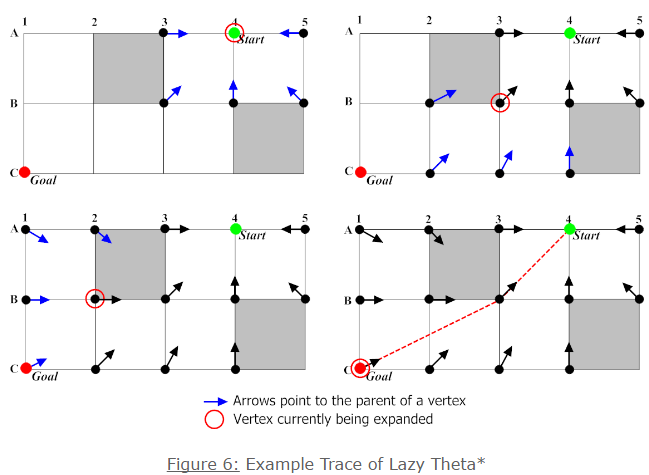
示例,注意右上图(第二步)中B2指向的是start而不是B3,因为B2尚未打开,我们可以乐观认为B2和父节点B3的父节点有LOS。这一假设在左下图(第三步)中,B2打开时才得到修正。
在Theta*中,检查视线的时机发生于一个点进入open列表的时候。但是实际上,有很多进入open列表的点最终不在路径中,这意味着LOS检查是无效的。因此Lazy Theta*选择把LOS检查放到打开该节点的时候进行。
当然,进入open列表的点,我们需要设置它的g值和parent。在Lazy Theta*中,我们乐观地认为在这里LOS检查永远成立的,因此g值和parent值得的设置按照Theta*中LOS检查成立一般地进行设置。
随后,在打开一个节点时,我们对这个点调用SetVertex方法。该方法中我们对该点和它的父节点进行真正的LOS检查。如果成立,那么我们之前的假设是对的,那就继续进行下去。如果没有LOS,那么我们还需要为这个点找到一个正确的parent。
对点s找到正确的parent的方法稍微繁杂一点。首先我们要知道什么点能成为s的parent,答案是在close表里的点。其次还应该是和s有LOS关系的点。如果有的选择的话,我们还要选择g(parent) + c(parent,s)最小的。
当然,如果我们对close表里的点全部做一遍LOS检查那就是本末倒置了。在这里我们直接取s的相邻点作为parent的候选。然后和close表做个交集,在其中选择最好的点即可。
Lazy Theta*的优化
这个优化是在A*中就存在的,优化的A*叫做Weighted A*,即带权重的A*。
所谓权重是加给启发函数的。原本的估值函数F(s) = G(s) + H(s),加入权重后变成F(s) = G(s) + weight * H(s) 。
这意味着比起从出发点到当前点的距离,当前点到终点的距离的估值影响更大(当weight > 1时)。
可以简单的理解为weight越大,会“更想接近终点”。
在Lazy Theta*中也可以直接套用这个优化。同时比起普通的weighted A*,Lazy Theta*中的这项优化更加有价值。具体的就不在这里叙述了,在原文中有提到。
下一篇文章中我会简单叙述一下我在unity/C#中实现的Lazy Theta*寻路。



