Recurrent Neural Networks vs LSTM
Recurrent Neural Network
RNN擅长处理序列问题。下面我们就来看看RNN的原理。
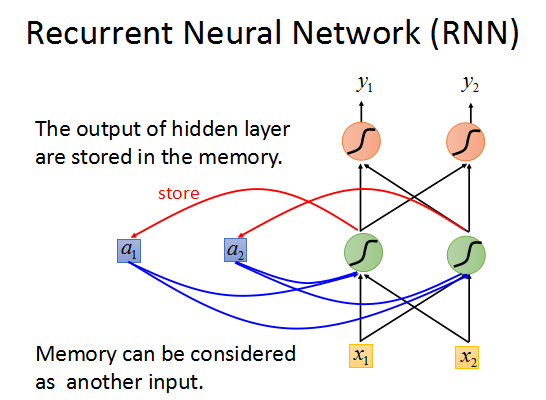
可以这样描述：如上图所述，网络的每一个output都会对应一个memory单元用于存储这一时刻网络的输出值，
然后这个memory会作为下一时刻输入的一部分传入RNN,如此循环下去。
下面来看一个例子。
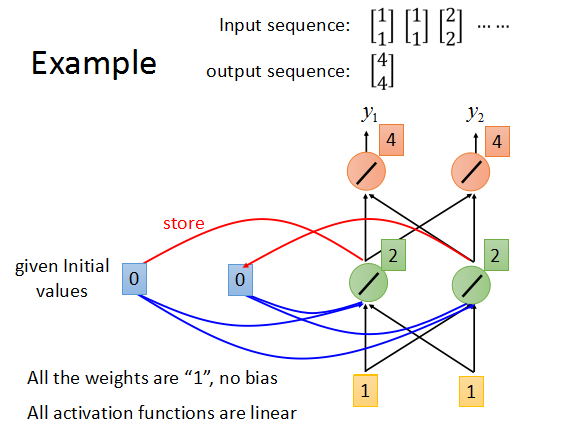
假设所有神经元的weight都为1，没有bias，所有激励函数都是linear，memory的初始值为0.
输入序列[1,1],[1,1],[2,2].....，来以此计算输出。
对输入[1，1]，output为1×1+1×1 + 0×1 = 2->2*1+2*1 = 4,最后输出为[4,4]，然后将[4,4]存入memory单元，作为下一时刻的部分输入。
最后得到的输出序列是这样的。
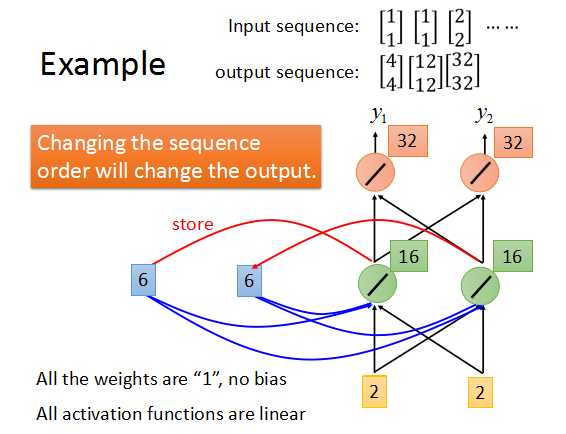
而如果每次输入的序列不同，最后的输出序列也会不一样。
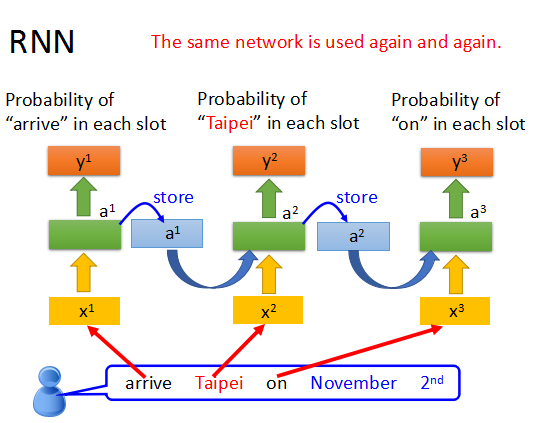
在RNN中，每次都是使用相同的网络结构，只是每次的输入和memory会不同。
这样就使我们在句子分析中，能够辨别同一个词出现在不同位置的时候的不同意思。
当然RNN也可以是深层的网络。这里会有两种不同的RNN类型Elman和Jordan。
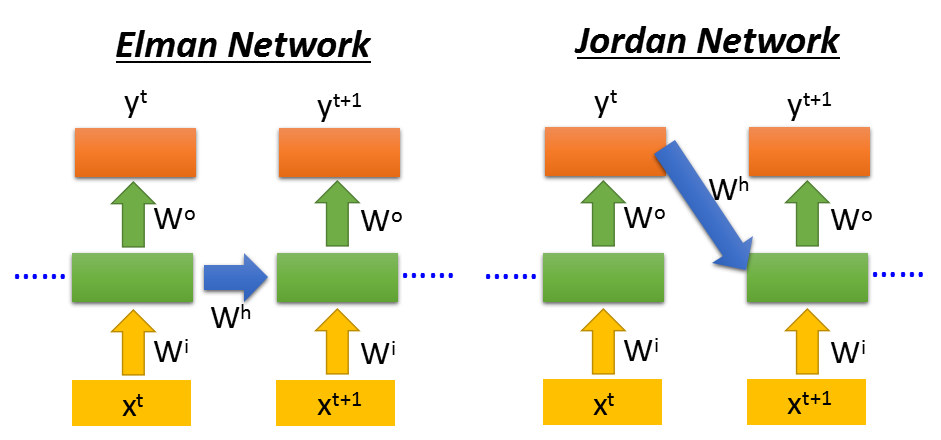
还有双向的RNN，可以兼顾句子的前后部分。
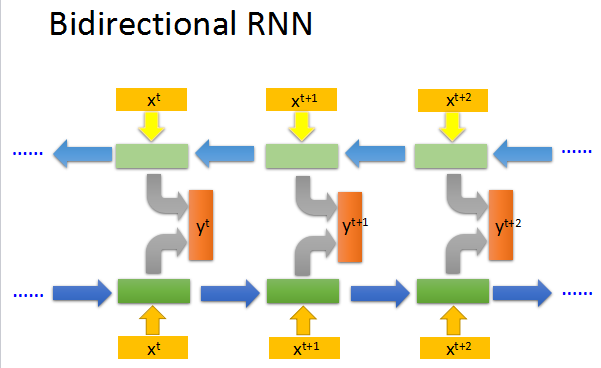
Long Short-term Memory (LSTM)
上面就是一个LSTM的cell的结构，每个cell有4个input， 和1个output。
其中3个input是3个gate。input gate 控制真的的input是否输入网络；
forget gate 控制memory是否要记得之前的时序信息；
output gate 控制是否输出当前的得到的output。
RNN cell的3个gate输入分别是zi,zf,zo，都是标量数据scalar，都需要通过一个激励函数f，f通常是sigmoid，可以将正负无穷的区间压缩到0～1，
模拟gate的开关。input z也是一个scalar，通过g(z)与f(zi)相乘，如果input gate关闭，就是f(zi)=0,那么输入g(z)就没有进入到cell中。
然后继续往下走，有c' = g(x)*f(zi) + c*f(zf), 如果forget gate的f(zf)为1，就相当于记得memory的值，可以加上c，然后将c‘存入到memory中。
真正的输出会是a = h(c')*f(zo),若f(zo)=0,则不输出当前值。
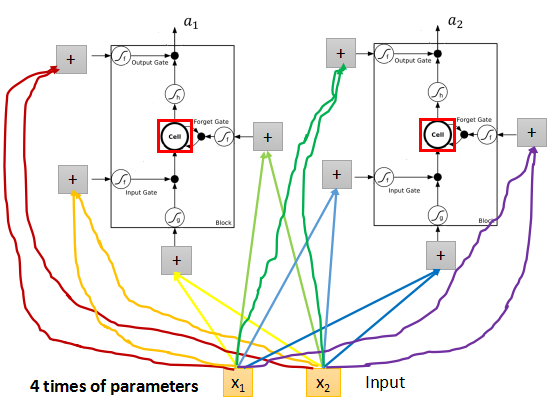
因为在RNN中需要处理4个input，所以参数会是传统前向传播网络的4倍。
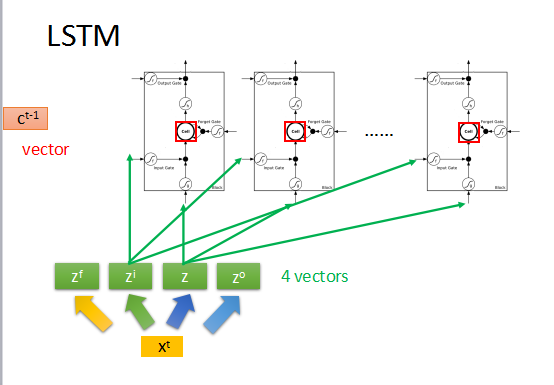
假如上一时刻memory的值为ct-1,是一个vector，输入为xt，然后转化为4个input向量。
首先zi通过activation function与z相乘，zf通过activation function与memory中的ct-1相乘，然后把这两个结果相加，得到新的memory中的值ct，
zo通过activation function与刚刚的输出相乘得到最终的输出yt。
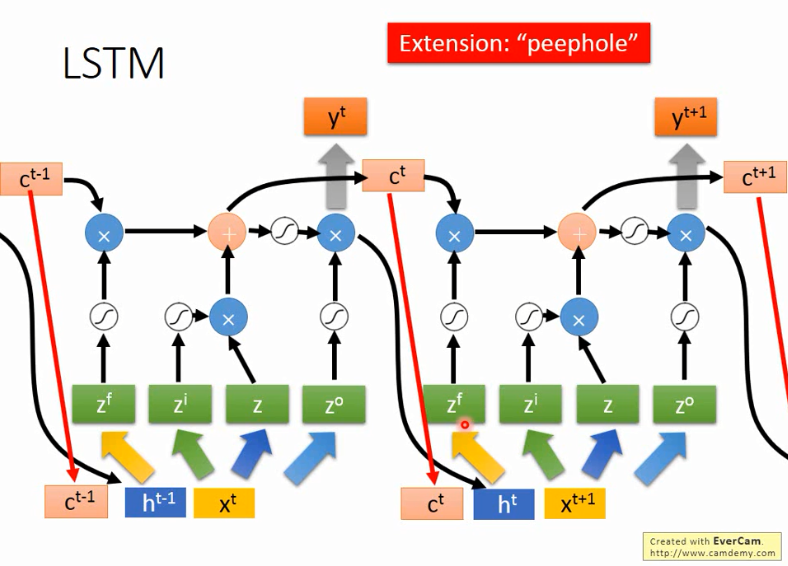
但是通常RNN还会将上一时刻的输出ht和memory中的值ct，再加上输入xt一起作为输入来操控RNN。如上图所示。
以上就是RNN和LSTM的基本原理。
RNN的训练
DNN和CNN都可以使用gradient decent 来训练，RNN也可以。
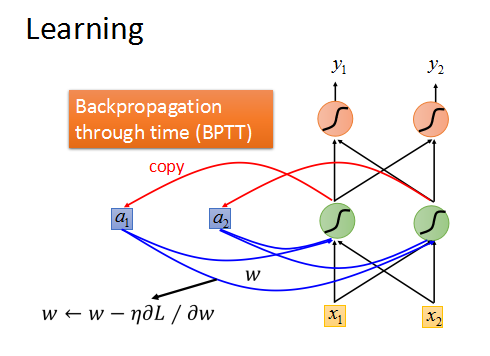
RNN是基于时间序列的Backpropagation through time(BPTT)。
但是训练结果通常是这样的：
RNN的total loss会发生剧烈的震荡，相当不稳定，无法收敛。
这是因为RNN的error surface 很崎岖，有平坦的地方，也有梯度很陡的地方。
这样就是梯度的变化很大，有时候参数w很小的更新就会造成很大的梯度变化，导致loss剧烈震荡。(clipping)
但是造成这种情况的原因并不是我们使用了sigmoid，而且在RNN上使用Relu往往会得到更坏的结果。
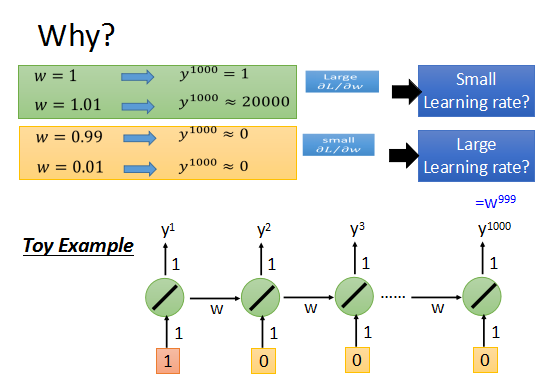
来看一个简单的例子，一个最简单的RNN。
参数w=1时，输出为1；参数w=1.01时，输出为20000.
w的变化对输出值有不同程度的影响，致使learning rate不好选择。
综上所述，RNN的训练很困难。
RNN很难训练，那有什么解决办法吗？那就是LSTM。
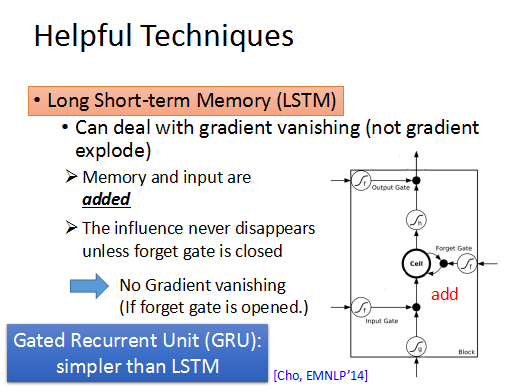
LSTM可以去掉error surface上“平坦”的地方，使梯度不至于特别小，这样可以解决梯度弥散的问题。
训练LSTM的时候，需要将learning rate 调整到很小。
简单的RNN每次训练后都会将memory中的信息覆盖，放入当前结果到memory中。
而LSTM是不一样的，它每次都将memory中的值乘上forget gate的值再加上input，放入cell，所以如果当前的w对memory有影响，那么这个影响将持续存在，在RNN中每个时刻的memory都会被覆盖，w的影响都不再存在。所以只要forget gate 一直打开，memory中的值都会被加到新的input中，而不会消失，这样就解决了gradient valish的问题。
